| A | B | C | D | E | F | |
| 問題文 | ■ | ■ | ■ | ■ | ■ | ■ |
| 自分の提出 | ■ | ■ | ■ | ■ | ■ | |
| 結果 | AC | AC | AC | AC | AC |
全体感想
最近はAtCoder上での練習はさぼっていますが、yukicoderをどんどん進めながら、作問作業に取り組んだり、言語アプデ後のことを勉強したり、離散数学まわりの専門書を読み進めたりしています。
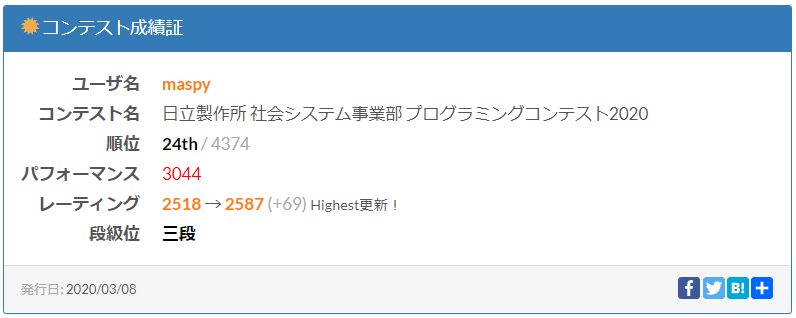
久しぶりのratedでした。5完 5ペナで、24位。初の赤パフォです。
解説いただきました。 https://t.co/EbVWiW33Nn
— maspy (@maspy_stars) March 8, 2020
期間的にもかなり空きましたから、銀パフォはかなり昔のようなイメージになっていて、赤パフォすら再現できない焦りに悩まされていました。そこそこ良い出来だと思っても赤パフォ未満なことが続いたので、「初赤パフォ」は冗談気味とはいえ、とてもとても嬉しいのは本当です。引き続き頑張ります。
考察での式変形ミスがなければ、ペナ込みで40分以上短縮できたはずなので心残りはありますが、ミスをするのもリカバリーに時間がかかっているのも実力不足ゆえですね。少しずつレベルアップしていきたいです。
立ち回り:A解く。B読む。自明すぎて勘違いしてそうな気になって先にCDEFを読む。Cを考察しながらBを読み直し、提出。その後、CEDの順に解きました。Fは歯が立たず。グラフの考察はまだ弱点な感じがします。
問題C – ThREE
$(1,1)$ と $(2,2)$ が距離3に来るのを避けるゲームです。
はじめは、距離3の点対がそんなに多くないのかな?と思いました。点対が多そうなときを考えます。次のようなグラフを思い浮かべました。
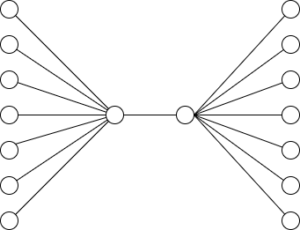
距離3点の点対が $\Theta(N^2)$ ということもあることが判明。このグラフで、$(1,1), (2,2)$ を回避できるかな?と考えていると、左端のグループに全部 $0$ または $1$ を、右端のグループに $0$ または $2$ を割り当てればよいことに気づきます(必要性としてすぐに出てくる条件 → 確かに十分性も満たしていることが検証できる)。
あとは速かったです。木が二部グラフという知識はあった(自明ですが)ので、一般の木で同様の構成ができないかを考えます。一方のサイズがとても大きい二部グラフでは、$(0,1)$ vs $(0,2)$ の構図にできないことに気づきますが、この場合にも片方を $0$ または $1$ の単色にすれば良いです(「ちょうど片方に全ての $1$ を割り当てる」のを考察でも実装でも特別視してしまいましたが、$(0,1)$ の 2色を当てていると見なせるので、余計な場合分けをしてしまいました。)
思考時には、頂点数が $8$ のときの、二部グラフの頂点数の内訳を全部書き出して、割り当てを考えました。
微妙に順列の復元を実装するところがミスしやすそうでしたが、場合分けのどれにも使える復元用の関数を実装したりして、上手く乗り切れたと思います。
問題D – Manga Market
最適解に仮定できる構造を探します。この際に、隣接する 2 つのお店の順序に構造を仮定できる場合があるというのが、過去問でも何度か出ている典型手法です(たとえば EDPC にも ABC にもあります)。初見時の感動は大きめだった手法なので、これをやる問題、好き。
時刻 $t$ から、店 $(a,b)$と $(a’,b’)$ を使ったときの終了時刻を計算します。$(a,b), (a’,b’)$ の使用順を逆転させた場合の終了時刻と比べることで、最適解ではこの2つの店がある順に並んでいると仮定できる可能性があります。具体的には、$(a,b), (a’,b’)$ の方が $(a’,b’), (a,b)$ よりも良いという条件を
- $f(a,b) \leqq f(a’,b’)$ の形($t$ に依存せず、変数分離可能)。
に変形できれば、$f$ をキーとしてソート順を仮定できます。問題の見た目から上手くいくと確信できる方法ではなくて、計算式を作ってみないと上手くいくか分からない考察ルートかと思います。
今回は、最適解のうちで、訪れた店が $\frac{a}{b+1}$ の降順であるものが存在することが分かります。これで、店の並び順は仮定した上で、各店を使う・使わないを調べる問題に帰着できました。
そこからがまた苦戦です。消費した店舗数に対する最適な消費時間を持つ dp を当然考えますが、一見すると状態数が多すぎます。たくさん来店しまくる場合もありうるよね…例えば……と考えていたら、実は時刻が急増するので来店数は増やせないことが分かって解決しました。
はじめ、計算ミスをしていて、ソートの比較条件を「$\frac{a}{b}$ の昇順」としていました。これで 1WA です。「84AC 1WA」の結果を見て、$N=1$ とか $T=0$ とかそういうところで何か抜かしたかな?と確認したり、問題文・サンプルを数周読み直したり、意図的に例外を発生させる提出デバッグを試みたりしていました。何度見直しても正しく実装できているように感じたので、考察を完全に1からなぞりなおしているとようやく気付きました。10WA単位で誤答が出ていたらもっと早く気づけたと思う、1WAのみで、こんな大事なところ失敗していると思わなかったw
python は完全な精度で整数の演算を行う多倍長整数を備えていますが、小数については一般的な 64bit 浮動小数点数です。
( 完全な精度で小数を持とうとすると、1/3 を小数計算した瞬間に無限のメモリが必要ですし仕方ない仕組みです。計算精度を高める方法としては例えば、高精度な十進法小数:decimal モジュール 、あるいは完全な精度で有理数を扱う fraction モジュール があります)。
64bit 浮動小数点数は、有効数字 53bit で、10進法でだいたい最高位から15桁以上先の計算は保証されません ($2^{53}$ は約 $10^{16}$)。 $a, b, a’, b’\leqq 10^9$ に対して $\frac{a}{b}$ と $\frac{a’}{b’}$ の比較をする際には、場合によっては $18$ 桁目付近を比べる必要があるため、分数を小数になおしての比較ソートは厳密な計算結果が保証されません($b, b’$ が $10^9$ 近くで、$|ab’ – a’b|=1$ ということがあります)。
そのため、整数の範囲で比較関数を実装して、ソートしました。
提出 → ■、参考 → ■
ただし、今回は小数でソートしても全てACになるようです。最適解は大きな $a,b$ のお店を多用しないため助かっているのかな?ただし上手くテストケースを作れば、今回の問題設定でも、小数でのソートはWAになるのではないかと思います……たぶん。
問題E – Odd Sum Rectangles
意外とスタンダードな考察の積み重ねという気がします。いろいろな区間和(矩形和)を観察せよという問題では、区間和を累積和により言い換える方法が、数えきれないほど出題のある定跡です。
累積和の性質を調べる問題に言い換えると、適切な4点対の個数を最大化する問題に化けます($4$ 点 $(i_1-1,i_2-1), (i_1-1,j_2), (j_1, i_2-1), (j_1,j_2)$)。この言い換えをする際に、第 $0$ 行と第 $0$ 列を $0$ 埋めして、$2^N\times 2^M$ のグリッドの問題にします(綺麗になって、正しい道を行けている気分になれました)。
4点対のうち、使用する2行を固定して観察すると、「奇妙さ」が、2行の和の偶奇の分布から計算できると分かります。特に、任意の $2$ 行の間のハミング距離が 列数の半分と一致するならば最大値であることが分かります。
ハミング距離の大きい符号族を得るというのは、符号理論 という情報科学分野での典型的な問題意識なので、あとは「符号」「ハミング距離」などでググって割とすぐに見つかりました。
冷静に考えるといくつかの数学解釈があって、
- $0, 1$ で埋める代わりに $1, -1$ で埋めると思うと、内積に関する直交関数の族を得る問題になる。これは、群の指標全体は直交関数系で、中でも $\F_2^M$ 上の指標は $\{-1,1\}$ に値を持つのでよい(Hadamard変換というものの関係者)。
- ベクトル空間 $\F_2^M$ において、原点を通る超平面を全部考える。任意の2枚の交わりが $M-2$ 次元部分空間なので、半分の点で交わっている(「線形符号」という符号族の構成)。
などの見方ができると十分なのかなと思いました。
コンテスト中も、ググる前にHadamard変換が頭を過ぎったのですが、直交性とハミング距離が似て非なるものだと思って棄却してしまった。けど、頭を過ぎっていたおかげで、ググって出てきたアダマール符号という単語にすぐフォーカス出来ましたね。

