| A | B | C | D | E | F | |
| 問題文 | ■ | ■ | ■ | ■ | ■ | ■ |
| 自分の提出 | ■ | ■ | ■ | ■ | ■ | |
| 結果 | AC | AC | AC | AC | AC |
全体感想
ちょうどABCとARCの間くらいの難易度だったように思います。
十分、全完をねらえたのですが、惜しくも5完止まりでした。Fで粗い実装をして、時間をかけてしまいましたね。
Fの初提出時点で、全完が居なかったこともあり、「最速実装+ノーミスで行ければチャンスがある!」と欲が出ました。結局、ひどいコードだったのでリファクタリングしながらバグ取りをして、かなり時間がかかってしまいました。まぁ、入賞確率の最大化という意味では間違った立ち回りではなかったかな?ちょっとリカバリーに時間かけすぎだけど。
Fがそんなに正答率出なさそうだったので、絶対通そうと思いました。Eはラスト15分で実装していましたが、右往左往してしまって数分間に合わず。22:39時点でかけていたコードの max を min に取り換えれば通るとかそういう惜しさでした。
Fを解いているので、順位はそれなりになるパターンです。
問題C – Sqrt Inequality
私は、整数計算で解説PDFのようにやりました。解説PDFの $(3)\implies (4)$ のような「両辺を $2$ 乗する」式変形は、符号を見ないと同値性が保たれないので、注意しましょう。
($A<B\iff A^2<B^2$ はうそ。$A,B\geqq 0$ の条件下でなら同値。)
こういうの、世の中高生もめちゃくちゃ間違えますよね。ひとつひとつ根拠を確認しながら式変形する癖を意識したいところです。
小数で扱う場合の計算誤差については、先週も記事にしたので、読者の方でそれが活きた人が居れば嬉しいなーとか思いましたが、どうでしょうか?Python で有効数字を増やしたければ、decimal モジュールを利用するのが簡単です。小数を1000桁まで計算したとしても、1000桁目を切り捨てて誤差が出たりしていると、両辺が完全に一致する場合に問題が生じます。やはり、適切な許容誤差 eps を設定して、計算しましょう。
提出例 → ■
小数できわどいことをやりたい場合は、どのくらいの精度まで計算しないといけないのかを見積もることが必要になります。今回の $\sqrt{}$ の線形結合の場合、以下のツイートツリーのようになります。
問題E – Three Substrings
コンテスト後提出:■
Aを基準にしたとき、B,C の位置せいぜい $\Theta(N)$ 通りくらいを見れば良さそうです。
「A、Bを配置した文字列 $O(|A|+|B|)$ 通りに対して、$C$ をくっつける問題を解く」みたいな方法を始めは考えたのですが、A, Bを組み合わせた文字列の列挙が地味に面倒に感じたりして。左右の位置関係も変わったり、間にオールマイティがはさまったり、微妙にややこしさがあります。簡単だけど細部までやり切るのがちょい手間なタイプ。(→ コンテスト中は、Fを考えたくなったのでそちらを優先していました。)
とりあえず、A,Bの配置については、Aから見たBの相対的な位置を持つことにして、「整数をひとつ選ぶ問題」として思考をなるべく簡潔にします。「Bの位置 $i$、Cの位置 $j$ であって、うまくかみ合うのもを探索せよ」となりました。
噛み合うかどうかの判定は、2種類ずつの文字について行えばよく、どの $2$ 種の文字のかみ合わせについてもありうる判定問題は $\Theta(N)$ 件なので、1件あたり $\Theta(N)$ かけて解けばよいです($N = |A| + |B| + |C|$ など)。
負の添字で混乱しそうになったので、A,B,Cの順序関係 6 通りを解く形で実装しました。探索幅が半分になったりするので、それほど無駄はしていないと思います。解説PDFでは、配列のインデックスをずらすことで、負数の扱いに対応しています。
ちょっと実装でまごついてしまったと思うので、後日解きなおしたいところです。
問題F – Fractal Shortest Path
以下、座標は $1$ ずつマイナスして、一番左上を $(0,0)$ と記述します。
$(a,b)$ と $(c,d)$ を、$|a-c| + |b-d|$ で結べるパターンが案外多いというのが最初の気づきでした。以下、このような経路を「無駄のない経路」と呼ぶことにします。たとえば、$(0,0)$ から任意のマス目には、そのような経路が存在することが、帰納的に証明できます。
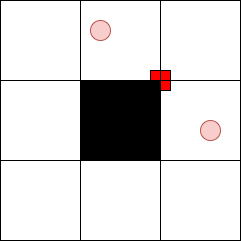
すると、レベル $K-1$ のフラクタルに分解したとき、行・列ともに異なるところにある2点間が、無駄のない経路で結べることが分かります。上図のように、各フラクタルの角を経由することにすれば、$(0,0)$ と各点を結べるという命題に帰着できます。
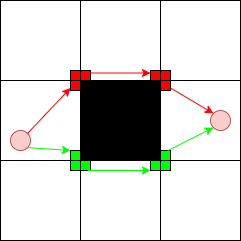
同じ行で、大きい■をまたぐ場合にも同じような性質が利用できます。レベル $K-1$ の■だけを見たときの最短経路が、より小さい■に邪魔されずに実現できることが、「角への移動は無駄なくできる」を利用することで証明できます。2通りに回り方を検証して、小さい方を返しましょう。
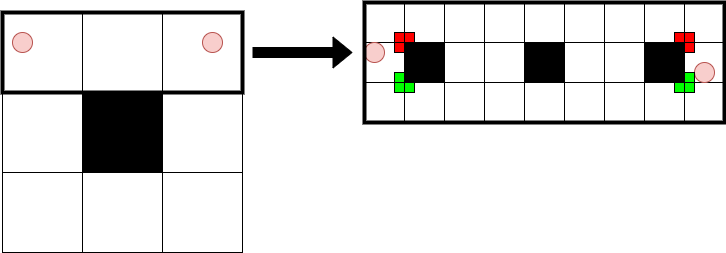
同じ行、かつ、レベル $K-1$ の■をまたがない場合には、もうひとつ小さい正方形を考慮します。そこでやはり、行も列も異なるならば、無駄のない経路が存在。■をはさんで同じ行にあるなら、その正方形を避ける以外は無駄のない経路が存在です。■をはさまず同じ行があるなら、さらに小さいレベルのフラクタルを考慮していきます。
主に正方形を $9$ 等分した図で考察していたため、「■をはさまず同じ行」の判定を、「同じ行かつ行番号が $\pmod{3}$ で 1」として失敗しました。
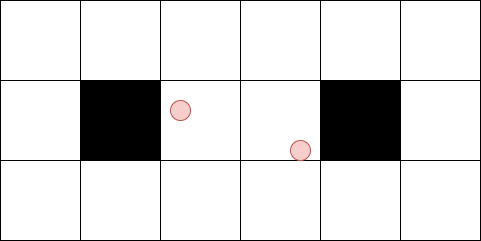
こういう場合も、もうひとつ小さい正方形を考慮していきます。

