
| A | B | C | D | E | F | |
| 問題文 | ■ | ■ | ■ | ■ | ■ | ■ |
| 自分の提出 | ■ | ■ | ■ | ■ | ||
| 結果 | AC | AC | AC | AC |
全体感想
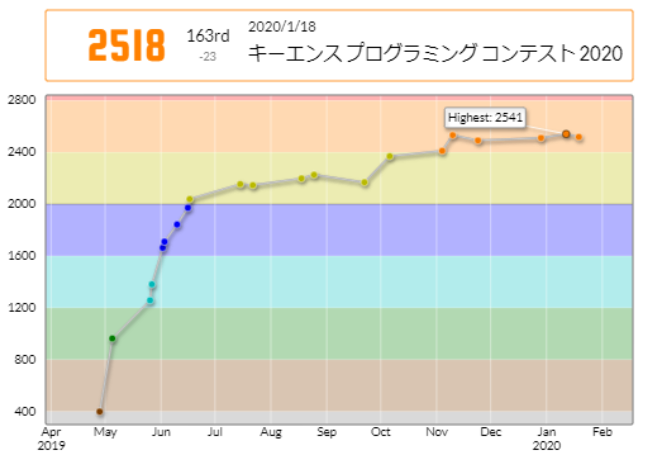
75分4完(ABCE)4ペナ、163位でした。
※ 問題D:123分時点でAC。3分オーバーでした。
ABCDの4完を上回れる点数の取り方なので、もう少し良い順位が出ると思っていたのですが、想像以上に5完が多くてレベルが高かったです。
パフォーマンス値はそんなに悲しむほど低くはないのですが、無難に乗り切ったつもりなのにいつもより低順位なのが、心配な気持ちにさせられますね。まぁ、確かに後から振り返ると無駄な失敗で時間かけすぎてはいます。
問題B – Robot Arms
少しだけ言い換えれば「区間スケジューリング」という有名問題の一種で、アリ本に序盤にも解説があります。区間の右端でソートしたあと、左から順に貪欲に選んでいけばよいです。(左端でソートして、右から順に貪欲してもよいです)。
ソートするため、計算量は$\Theta(N \log N)$です。
問題C – Subarray Sum
え。
長さ$1$の区間で$S$を確保して、他に$S$を作らないようにすればよいです。
・[S, S, S, S, INF, INF, INF]
のような作り方をしたいですが、制約から $S = 10^9$ の場合に $S$ より大きい数がとれず。その場合は $[S,S,S,1,1,1,1,1]$ のようにすればよいです。
結局「区間和」という設定はほとんど活きない問題。
問題D – Swap and Flip
考察の起点は、「各カードの到達位置を決めると、到達時点での表裏が決まる」というものです。より詳しく考えると、「各カードの到達位置の偶奇を決めると、最終的な表裏が決まる」となります。
したがって、偶数・奇数位置に並ぶカードの集合を決め打ってしまえば簡単な問題になります。
偶数グループ・奇数グループそれぞれで昇順に並ぶ必要があります。そうすると、まず(カードの並びではなく)数値の並びが高々1通りに限定されます。これが全体で見て昇順になってくれるかどうかで、判定問題が解けます。
あとは、隣接互換の回数の最小化をします。ある順に並び替えを行うための隣接互換の最小回数を求めるのは有名問題で、転倒数 とよばれる値になります。これは、並べ替え前の順序と、並べ替え後の順序で左右が入れ替わっている2数の組の個数で、$0$ 以上 $\frac{N(N-1)}{2}$ の間の数値になります。
転倒数の計算を考えると、「等しい数が書かれたカードについては、元のインデックスの昇順に並べるのが最適」だと分かります。したがって、偶数グループ・奇数グループを組 (カードの数値・元のインデックス) についてソートした上で判定問題・転倒数の計算を行えばよいことになります。
転倒数の計算には、BIT(Fenwick tree)を用いる方法・マージソートをしながら計算するものが有名で、計算量 $\Theta(N \log N)$ の計算が可能です。
全体としては、$\Theta(\binom{N}{\lfloor N/2\rfloor}\cdot N\log N)$ の計算量になります。
※ コンテスト後提出 → ■
二項係数のオーダー
計算量には、$\binom{18}{9}$ のような数が出てきます。二項係数の真ん中の大きさは、$\binom{N}{\lfloor N/2\rfloor} = \Theta(2^N/\sqrt{N})$ という評価が可能です。例えば
- スターリングの公式 $N! \sim \sqrt{2\pi N}\bigl(\frac{e}{N}\bigr)^N$ を用いる
- 二項分布 $B(N,0.5)$ が正規分布で近似できること、その標準偏差が$\Theta(\sqrt{N})$ である(二項係数の和が $2^N$ で、その大部分が $\Theta(\sqrt{N})$ の幅に集中して分布する)ことから分かる
などの説明があります。とはいえ指数増加するので計算量評価で巨大な $N$ に対する二項係数が出てくることはなくて、計算量の評価をする場合には実際に計算してみればよいです。
問題E – Bichromization
これもなー、「他の色の頂点への最短路」という設定があんまり活きない感じの結論になってしまったなという。
黒と白を結ぶ重み最小の辺を考えます。これは、必ずその両端の整数として採用されることが分かります。したがって重み最小の頂点が隣接していると詰みで、そこの間をその重みで結びます。
何か良いルールが見つかったら、なるべく一般化することを考えるという原則に沿って、考察を広げます。ある頂点 $v$ の隣接頂点に、重みが $D_v$ 以下であるような頂点が存在しなければ詰むことが分かります。また、隣接頂点の重みの最小値が $D_v$ と一致していれば、その重さで結ぶことになるということも分かります。
自明な必要条件、および、構築の第一歩ができてきました。あとはこれを詰めていけば完成です。構築においては、既に上手くいくように定めた頂点については、より重い辺であれば結び放題だというのが肝要です。
軽い頂点から構築していって、頂点 $v$ はより軽い頂点 $w$ と結ばれている場合、辺 $vw$ を重さ $D_v$ にしていけばよいです。結局各頂点に対して、1つの辺だけで条件を達成できて、残りは $10^9$ で埋めてしまえば完成です。

