| A | B | C | D | E | F | |
| 問題文 | ■ | ■ | ■ | ■ | ■ | ■ |
| 自分の提出 | ■ | ■ | ■ | ■ | ||
| 結果 | AC | AC | AC | AC |
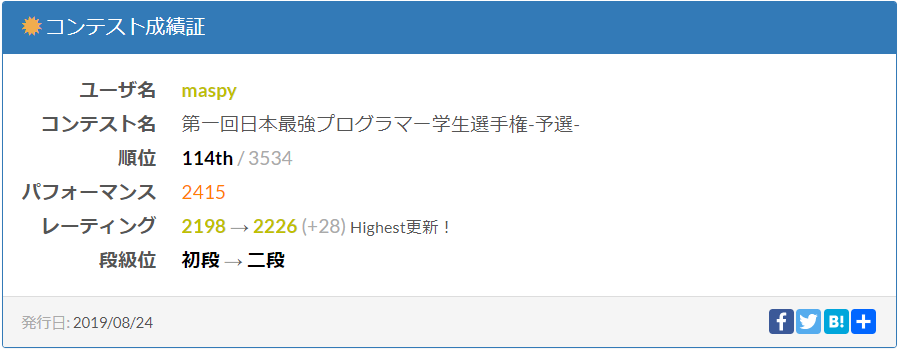
全体感想
45分4完(1ペナルティ)で114位でした。
問題Fが解けそうだったので、考えていました。方針が立って、あとは細部の計算を確認しながら実装するだけ!となったのが終了15分前。細かい計算ミスなどをチェックする余裕がほとんどないまま残り1分くらいで実装できましたが、サンプルが合わずダメでしたw
終了後の検証でちゃんとACできたので、制限時間の問題ではあったようです。こういう得意寄りの問題を正解に結び付けていかないと上位には行きづらいですね。この問題なら3回に1回くらいはコンテスト中に解ききれると思うのですが…いつもそういう言い訳しているような(笑)
問題B – Kleene Inversion
300点の配点ですが、例えばABCコンテストの300点と比べるとだいぶ難易度が高いように思います。転倒数は条件を満たす2つ組の数え上げですが、何らかの形でまとめて数えたいです。例えば2つ組の片方を固定して数えるのが通常の考え方です。今回はさらに、同じパターンの並びを繰り返すことを使わないと計算量が爆発しそうです(1つの数を1回読むだけでTLEする)。
[3 1 4 1 5 9 2] [3 1 4 1 5 9 2] [3 1 4 1 5 9 2]
例えば、[3,1,4,1,5,9,2] × 3という並びの、3グループ目の「1」から見た転倒数です。
1,2グループ目からは同じ位置の5つが数え上げられ、3グループ目だけ例外的となっています。ここから
・異なるグループ間の転倒数 → 自身より小さい数値が1周期にいくつ含まれているか。
・同グループ内の転倒数
に分けて計算するという発想になります。
・異なるグループ間の転倒数 → 自身より小さい数値が1周期にいくつ含まれているか。
・同グループ内の転倒数 → 周期内の自身より左に小さい数値がいくつ含まれているか。
それぞれある程度下手に計算しても、$O(N^2)$ で間に合います。転倒数には、BIT(fenwick tree)などを用いて$O(N\log N)$で計算する方法もあります。今回の問題では不要ですが、過去問のARC-Cクラスでは必須となっているようです。「BIT 転倒数」などでぐぐりましょう。
問題C – Cell Inversion
奇サイクルがないという条件は、二部グラフと同値であることは知っていました。完全グラフを二部グラフに分割する問題です。
単純に大きい二部グラフを取り去ろうとすると、$2n$ 頂点から、完全二部グラフ $K_{n,n}$ を取り去れます。これは辺の数が$\frac{1}{2}{}_{2n}\mathrm{C}_{2}$ 程度なので、レベル2つくらいで出来るのかな?というのが第一印象でした。
これを実験していると、5頂点の場合に失敗します。(1,2,3),(4,5) と分割して完全二部グラフをとっても補グラフに完全グラフ $K_2, K_3$ が残ります。完全二部グラフよりも小さい辺集合をとると、さらに状況が悪くなります。
この辺を試しながら、5頂点で2レベルが無理であることの証明を検討しているうちに、「$K_{2n}$ 完全グラフに対してひとつ二部グラフを取り去ったときに、補グラフに必ず $K_n$ 完全グラフが含まれる」ことに気づきました。
$2^n$ 頂点ならレベル $n$ 以上必要ということが分かります。実例構成もこの考え方の隣に落ちていました。初手で $2^n$ 元集合をぴったり2分割したあと、2手目はさらに残った $2^{n-1}$ 元集合をぴったり2分割することが必要そうだと気づきます。結局、1手目で二部グラフのどちらに入れるか、2手目で二部グラフのどちらに入れるか、…、$n$ 手目で二部グラフのどちらに入れるかという選択 $2^n$ 通りが、頂点 $2^n$ 通りでばらけていなければいけません。
これは逆に選択 $2^n$ 通りに対して頂点をひとつ持ってくることで達成できて、要するに自然数の $2$ 進法表示を各レベルの二部グラフの分割に対応させていけばよいと分かります。
問題F – Candy Retribution
コンテスト中には、解ききれず。$M$ 番目、$M+1$ 番目が数 $k$ であるとして、$k$ での場合分けによる分析を長く進めていました。このとき、$k$ がいくつあるかという余計なパラメータが入ってなかなか簡単にならず。そのうち、余事象側の方が簡単であることに気づきます。
固定された $k$ に対して余事象の方が簡単だと気づきますが、すると最初から余事象を考えればよいと気づきます。ここに気づいてからは、形式的べき級数を書いて5分くらいで方針が立ちました。
方針が立ったのが終了15分前で解ききれず。なんで余事象を考えるまでに30分以上かかっているのか…という反省点がありますが、まぁ仕方ないかな。
公式解説とも方針が異なりそうだったので、別記事で解説を書きました。良ければこちらをご覧ください。

