概要
問題文 → ■
公式解説 → なさそう
解法
必要条件
- 連結であることが必要です。
- MST の辺の重みの和が、頂点の重みの総和以上であることが必要です。
十分性 + 構築アルゴリズム
以上の必要条件は十分条件になっていることを確かめましょう。初めから全域木以外の辺は無視して、グラフは木であるとします。
まず操作は、辺縮約と言い換えられます。重み $a, b$ の頂点を結ぶ重み $c$ の辺を縮約すると、新たに重み $a+b-c$ の頂点ができると言い換えます。
次に、操作は「必要条件」を保つことが確かめられます。つまり、操作前の木が「必要条件」を満たすならば、操作後の木も「必要条件」を満たすことが分かります。
したがって、「必要条件のもと、頂点数が $2$ 以上の木において操作対象とできる辺が存在する」ことを示せばよいです。これは、帰納法と合わせて次のようにして確かめられます。
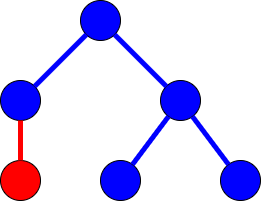
ひとつの葉と、それに接続する辺の組に注目します。
- 「葉の重み $\geq$ 辺の重み」 ならば、ここを辺縮約できます。
- そうでない場合、「これらの頂点と辺を除いた部分」が「必要条件」を満たすことになります。よって、帰納法の仮定をしておけば、この部分が $1$ 点になるまで操作可能であることが分かります。
構築アルゴリズムも同じです。葉に注目して、縮約可能ならば縮約してしまう。そうでないならば、残りの部分木に対する問題を再帰的に解いたあとで、今注目している辺を最後に縮約します。
コメント
「十分性の証明」に関して、証明の方針によっては構築アルゴリズムにつながらず苦労するかもしれません(私はこれのせいで、しばらく $O(N^2)$ 解法につかまりました)。
証明やアルゴリズムを考える上では、「木を考えてみる」「パスやスターを考えてみる」といった典型的な思考法が役に立ちました。

