概要
公式解説が読み解けておらず…。
木の圧縮パートを除くと大差ないかもしれません。なかなか実装が大変になってしまいました。
解法
グラフの変形
葉を縮約していきます。葉に接続する辺の寄与は、その両側にいくつの頂点があるかが分かれば計算できるので、それを答に足していきます。
葉に接続する辺の寄与を処理し終わっても、頂点を完全に削除してはダメです。辺を重み $0$ のものに置き換えるイメージでしょうか?頂点に対して、いくつの頂点が縮約されたものかを表す重みをもたせます。
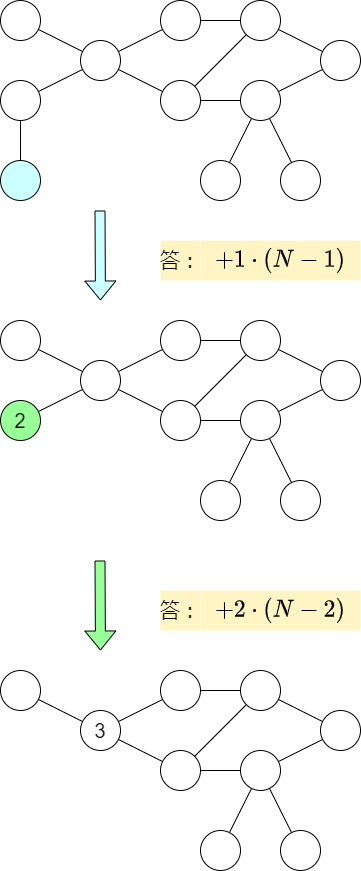
この操作の結果、$M – N$ の値と連結性は維持されたまま、グラフが次数 $1$ の頂点を持たない状態になります。
特別な頂点
葉を縮約してしまうと、次数 $1$ の頂点を持たない連結グラフの場合の計算に帰着されました。残った頂点数が $1$ であれば(これは、元が木のとき)、これで計算終了です。
そうでない場合、連結性よりすべての頂点の次数は $2$ 以上です。次数 $3$ 以上の頂点を特別な頂点として、その個数を $K$ と書きます。
頂点や辺の個数を $N, M$ と書けば、$\sum_{v} \deg(v) = 2M \geq 2(N + 777)$ ですから、次数 $3$ 以上の頂点は高々 $2\cdot 777$ 個しか存在しません:$K\leq 2\cdot 777$。
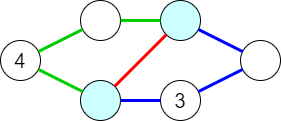
なお、$N = M$ のときにはサイクル $1$ つが残り、特別な頂点がひとつもなくなります。ひとつ特別な頂点を選んで $K = 1$ として扱えば、以下同じように解くことができます。
グラフ全体としては、特別な頂点 $K$ 個が、$O(M-N)$ 個のパスによって互いに結ばれている形になります。これらのパスも列挙しておきましょう。
- パスは $O(M-N)$ 個
- パスの長さの和は $O(N)$
となります。頂点は、「特別な頂点」「パスの内点」の $2$ 種がありますので、これらで場合分けしながら答を計算していきます。
葉を圧縮した関係で、$vw$ 間の距離に対して重み $C[v]C[w]$ をかけて加算していくといった形の計算を行います。
特別な頂点同士の距離
事前にパスを列挙しておいて、その距離をまとめて計算してしまうことで、Dijkstra 法などにより全点対最短距離が $O((M-N)^2\log (M-N))$ 時間で計算できます。
特別な頂点と、パスの内点の距離の計算
パスの両端点から、注目している特別な頂点までの距離は、事前計算されています。すると、パスの内点から特別な頂点までの距離も、計算できます(パスのどちら側に進むかに応じて、$2$ 通りの $\min$ です)。
パスの内点は全部で $O(N)$ 個。特別な頂点は $O(M-N)$ 個なので、この部分は全体で $O(N(M-N))$ 時間です。
累積和によって計算量を落とすことも可能です(全体の計算量オーダーには影響しませんが、定数倍改善になるでしょう)。
同じパスの内点同士の距離
同じパスの内点同士であっても、最短路はそのパスの外側を通る可能性があるので、多少厄介です。
パスの長さを $n$ として、$i$ 番目の頂点の重み $A[i]$ と書くと、次の形の計算になります:
- すべての $0\leq i < j\leq n$ に対する、$A[i]A[j]\cdot \min\{j-i, i-j+a\}$ の和を求めよ。
これを例えば $j$ を固定して、$j$ ごとに $O(1)$ 時間で計算しましょう。$\min$ でどちら側が選ばれるかは $i$ の範囲によって変わり、$\sum_{i} A[i] (j-i)$ や $\sum_{i}A[i](i-j+a)$ の形の区間和を計算できればよいことになります。この区間和は、$A[i]$ や $iA[i]$ の累積和を計算しておけば $O(1)$ 時間で計算できます。
よって、「同じパスの内点同士の距離」の寄与は、長さ $n$ のパスに対して $O(n)$ 時間で計算できます。すべてのパスを合わせて、このパートは $O(N)$ 時間です。
異なるパスの内点同士の計算
それぞれのパスの長さを、$n, m$ とすると、次の形の計算に帰着されます:
- $0\leq i < n, 0\leq j < m$ に対して $A[i]B[j]\cdot \min\{i+j+a,i-j+b,-i+j+c,-i-j+d\}$ の和を求めよ
この係数は、$j$ を決め打てば、$\min\{i+s,-i+t\}$ の形です。したがってやはり、$A[i]$ や $iA[i]$ の累積和を事前計算しておくことで、$j$ ごとの $O(1)$ 時間で計算できます。
あるパスに対して、相手のパスと $j$ の組をすべて試すと結局 $O(N)$ 通りの計算をすることになり、
ひとつのパスの寄与は $O(n+N)$ 時間です。すべてのパスの組に対してこれを行うと、$O(N + (M-N)N)$ 時間となります。
コメント
最近解いた問題:https://atcoder.jp/contests/pakencamp-2018-day2/tasks/pakencamp_2018_day2_g
と似たところが問われている問題。私は本記事の問題の方が、苦戦しました。
どちらも何らかの手法でグラフを圧縮することになりますが、解説の手法?(ちゃんと定義されていないように見えるが、木に追加する辺の端点や、その部分集合の LCA として書ける頂点を特別視かな?)と比べて、私の試みた葉やパスの縮約の方が、頂点数が少なく抑えられているようです。

