概要
シンプルなボス問。大体何をやればよいかはすぐに分かると思いますが、重複や漏れがなく実装しやすい形で計算できるかが問われていますね。
解法
出来上がる絵の連結成分の個数ごとに数えます。
矩形領域ごとの和への分割
例えば、$A = [3, 6, 9]$ として、連結成分が $2$ つの絵としてどのようなものがあるのかを考えます。
連結成分が $2$ つの場合、それぞれの成分にどの区間が含まれているかで場合分けをします。それぞれ、どのような長さの組合せが可能かを考えていくと、
- (3), (6,9) → 長さの組合せは、$[3,3] \times [9,15]$
- (6), (3,9) → 長さの組合せは、$[6,6]\times [9,12]$
- (9), (3,6) → 長さの組合せは、$[9,9]\times [6,9]$
- (6,9), (3) → 長さの組合せは、$[9,15]\times [3,3]$
- (3,9), (6) → 長さの組合せは、$[9,12]\times [6,6]$
- (3,6), (9) → 長さの組合せは、$[6,9]\times [9,9]$
これらの矩形領域の和集合が、実現できる長さの組となります。
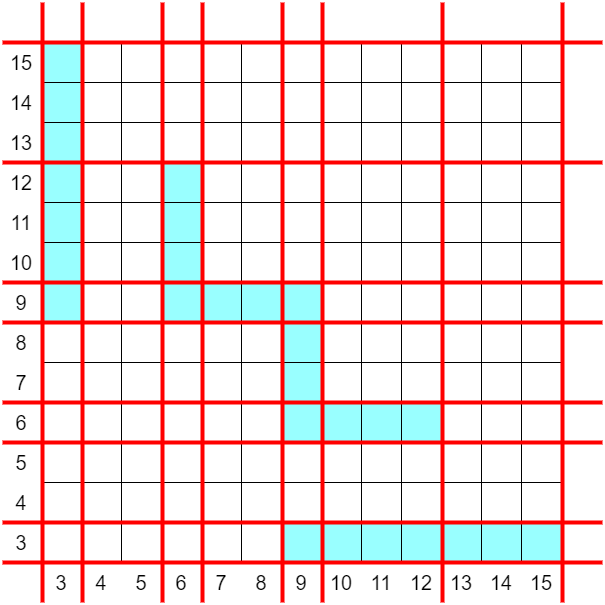
区間の端点の座標を使って座標圧縮すると、整数の $2$ つ組 $(x,y)$ 全体が定数個の領域に分割され、$(x,y)$ が集計対象となるか領域ごとに定まります(累積和を使う判定方法が有名ですが、愚直にひとつひとつの場合に含まれているかを確認しても十分高速です)。
結局、次の形の問題に帰着できることが分かります。
各 $(x,y)\in [a,b) \times [c,d)$ に対して、長さ $x$、長さ $y$ の連結成分を並べる方法の個数を計算し、その総和を求めよ
連結成分が $3$ つできるは、$3$ 次元の矩形領域について同様の問題を解くことになります。
矩形和の取り扱い
$[a,b) = [a,\infty) – [b,\infty)$ と包除原理より、次が解ければよいです。$[a,b)\times [c,d)$ に対する集計を行うには、次が行えればよいです。
各 $(x,y)\in [a,\infty) \times [c,\infty)$ に対して、長さ $x$、長さ $y$ の連結成分を並べる方法の個数を計算し、その総和を求めよ
- 左側に余るマス目の個数を $x_1$
- ひとつめの連結成分の長さを $a + x_2$
- 真ん中に余るマス目の個数を $1 + x_3$
- ふたつめの連結成分の長さを $c + x_4$
- 右端に余るマス目の個数を $x_5$
とおくと、これは $N – a – c – 1 = x_1 + x_2 + x_3 + x_4 + x_5$ を満たす非負整数 $(x_1,x_2,x_3,x_4,x_5)$ の数え上げに帰着されるため、適当な二項係数としてこれを計算することができます。

