概要
問題文 → ■
公式解説 → なさそう?(http://miz-miz.biz/contests/k4pc/commentary/)
自分の提出 → ■

G だけ解説がなさそうなので、書きます。
解法
基本方針
問われているものは、各項が整数で $A_i\leq X_i\leq B_i$ を満たす等差数列 $\{X_i\}$ の数え上げです。このような等差数列はある $p,q\in \Z$ を用いて $X_i = pi + q$ を書けるので、$A_i\leq pi + q\leq B_i$ を満たす $(p,q)\in \Z^2$ を数え上げる問題です($N\geq 2$ であるため、異なる $(p,q)$ が同じ等差数列を与えることはありません) 。
さらに不等式を、$pi – B_i \leq b\leq pi – A_i$ と書きかえます。これが任意の $i$ について成り立つという条件なので、$$\max_i pi – B_i\leq b\leq \min_i pi – A_i$$ と見ることにしましょう。$f(a) := \min_i A_i-pi$, $g(a) := \min_i B_i-pi$ として、数列を $a$ ごとに数え上げることにすれば、答は
$$\sum_{a\in\Z} \max(0, f(a) – g(a) + 1)$$
と書けることが分かります。
凸包
$f(a)$ は、数列 $A$ の上側凸包から計算できます。$xy$ 平面上に点 $(i,A_i)$ をプロットして、上側凸包を求めます。
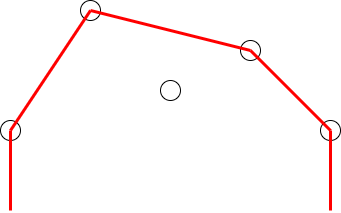
凸包は、頂点集合をスタックで管理して、$i$ が昇順に点の削除・追加をしていくことで線形時間で求めることができます。
頂点 $(i, A_i)$ が凸包上に現れていて、傾き $L_i, R_i$ の線分ではさまれているとしましょう。$i = 1, N$ に対しては $L_i = \infty$, $R_i = -\infty$ などとします。このとき、
$L_i\geq a \geq R_i \implies f(p) = pi – A_i$ であることが分かります。特に、$f$ は有限個の区間ごとに $1$ 次関数の規則になることが分かりました。
同様に、数列 $B$ の下側凸包を計算することで、$g(p)$ が区間ごとに $1$ 次関数の規則であることが分かります。
まとめ
本問題は、次の手順で解くことができます。
- 数列 $A$ の上側凸包、$B$ の下側凸包を求める。
- $f(p)$, $g(p)$ が、どのような区間でどのような $1$ 次関数になっているかを調べる。
- $f, g$ の規則の変化点で区切られた区間ごとに、$\sum_p\max(0, f(p) – g(p) + 1)$ を計算する(等差数列の和なので、$O(1)$ 時間で可能)。
$f, g$ の規則の変化点をマージして昇順に並べるところをマージソートの要領でやれば、全体として $O(N)$ 時間で解くことができます。
コメント
AC 人数の少ないボス問ですが、わりと基本手法だと思います。なお、$f(p) := \min_i (pi – A_i)$ と定義しましたが、これは数列 $A$ の Fenchel 変換(凸共役)と呼ばれる概念になります。

