概要
解法
$n$ が平方数でなければ、不可能です。$n-1\to n$ という操作を行う必要がありますが、そのあと操作できなくて詰みです。以下、$n$ を平方数とします。このとき、次のような操作手順が最適解のひとつを与えます。赤線が、$x\to \sqrt{x}$ という操作を表しています。
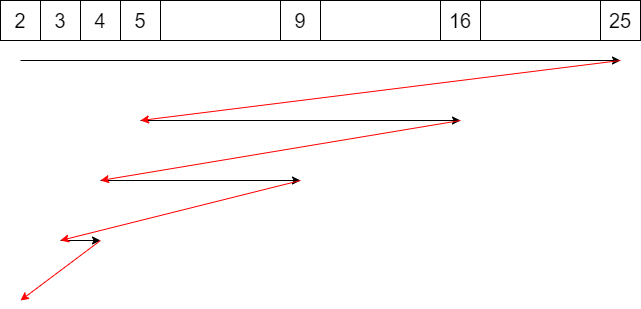
つまり、$n = m^2$ として、$k=m,m-1,\ldots,2$ の順に、
- $k^2$ までインクリメントしたあと、$k$ にすすむ
を繰り返します。任意の $k\geq 3$ に対して $k \leq (k-1)^2$ が成り立つことから、このような操作は可能です。
最適性は次のように示されます。操作 $x\to \sqrt{x}$ での「左移動距離」の総和を考えます。これは、少なくとも $\sum_{k=2}^m (k^2-k)$ 以上です。したがって、全体を通しての「右移動距離」の総和も$\sum_{k=2}^m (k^2-k)$ 以上です。
- 右移動回数は、$\sum_{k=2}^m (k^2-k)$ 以上
- 左移動回数は、$m-1$ 回以上
となりますが、上記の操作列は下からの評価を実現しているので、最適な操作列のひとつとなります。

