
| A | B | C | D | E | F | |
| 問題文 | ■ | ■ | ■ | ■ | ■ | ■ |
| 自分の提出 | ■ | ■ | ■ | ■ | ■ | ■ |
| 結果 | AC | AC | AC | AC | AC | WA |
問題F コンテスト後AC → https://atcoder.jp/contests/arc107/submissions/17763834
全体感想
49分5完、19位の成績でした。
A → B → (Cすぐに分からないのでDへ) → D → CEFを読む。問題Cは、$2$ マススワップと勘違いしていてめちゃくちゃ難しそうに見えていただけでした。
E, F を見比べて、面白そうな E から。面白かったです。AGC-B~C にありそう。
問題 F にかけられる時間が 50 分あり、解法の目途もすぐに立ったのですが、嘘考察を混ぜてしまっていたり、細かい実装に手間取ったりして、実装終わりで残り 10 分。
問題 F が解けていれば、たぶん赤レートに届いていたんですよね。実力不足で目標パフォに不足したり、レーティングが下がったりしても別に構わないんですけど、今回の問題 F については、過去に意識して出来るようにした種類の問題だったはずなので、結構悔しいところです。
ABCDF に負ける得点だったこと、問題 F は橙レート上位はかなりの人数が解くやつだと思ったことから、いまいちな順位を覚悟したのですが、予想以上のパフォーマンスが出ていて安心しました。難易度逆転という評価になっても不思議ではないと思ったけど、手前から解くに拘った方が多かったのかな?
問題D – Number of Multisets
これはすぐに解けました。答を $\dp[N,K]$ とおきます。
場合分け軸を何にするかですが、$1$ をいくつか使うかで考えます。$1$ を $i$ 個使うとすると、$1/2, 1/4, 1/8, \ldots$ から $N-i$ 個で $K-i$ を作るゲームが残ります。これは、$1, 1/2, 1/4, \ldots$ を $N-i$ 個使って $2(K-i)$ を作ることと対応がつくので、$$\dp[N,K] = \sum_{i=0}^{\infty}\dp[N-i,2(K-i)]$$ という漸化式が得られます。
これだと、$\dp[N,K]$ の計算に $\dp[N-1,2K]$ したがって $\dp[N-2,4K], \ldots, \dp[0, 2^{N}K]$ あたりが必要になりそうですが、$N < K\implies dp[N,K] = 0$ であることに気づけば、まずは $\Theta(N^3)$ 解法ができあがります。
dp[0,0] = 1
for n in range(N+1):
for k in range(N+1):
for i in range(k+1):
if n-i >= 2*(k-i):
dp[n,k] += dp[n-i,2*(k-i)]
ans = dp[N,K]という要領です。あとは、これを高速化するだけです。新たに足しこむ部分の累積和を作っておけば、高速化できます。
累積和をとっても良いですが、結局ひとつ項数の少ない累積和が dp テーブルのどこかにあるはずで、それを考えると $$\dp[n,k] = \dp[n-1,s-1] + \dp[n,2s]$$ というよりシンプルな計算式になりました。これは、元の問題に対して「$1$ をいくつ使うか」ではなく、「$1$ をひとつ以上使うのか、ひとつも使わないのか」で場合分けをしていることとも対応します。
問題E – Mex Mat
面白い問題でした。まずは手計算でサンプル理解。次にもう少し大きい場合を手計算。何か言えることを考えます。まずは
- $2$ 行目以降では、同じ数が隣合わせにはならない
ことに、すぐに気づきました。何か役に立ちそうなので、その性質に注目してもうちょっと考えます。
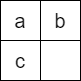
埋め途中。$a\neq b$ であることが分かっているとします。$a\neq b, c$ です。ここからまず、$a = 0$ ならば、右下に $0$ が入ることが分かります。つまり、
- $2$ 行目以降では、$0$ の右下には $0$ が来る
ということが分かりました。$0$ がたくさんあるといっぱい確定して嬉しいなと思いながら考察します。隣り合う数が相異なる行のうち、$0$ が少なそうなパターンを考えました。

$0$ の右下が $0$ であることを利用しつつ、$0$ の間のギャップが大きくなるパターンを考えると、この形です。手計算するとその次の行は $0$ のギャップが小さいことが分かります。
- $3$ 行目以降では、$0$ と $0$ の間隔は $3$ 以下っぽい
- $0$ が右下に続いていくのだから、間の部分ごとに問題を切り分けて、簡単なパターンに問題を分解できそう
- 解けそう
とこの辺で思いました。
考察内容の確認や、思考の整理も兼ねて、行の愚直更新を実装して、ランダムケースを観察しました。
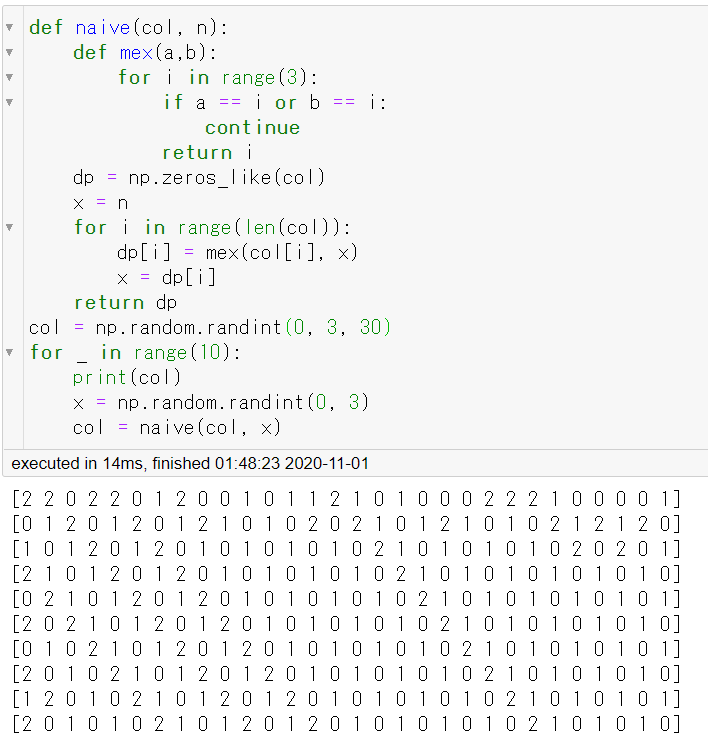
これ、コンテスト中に実装したコードで、提出にも残っているんですけど。ランダムなので実行ごとに新しいサンプルをくれますから、観察がはかどります。既に考察した
- 2 行目では、隣接 $2$ 数が相異なる
- 3 行目では、$2$ 回または $3$ 回ごとに $0$ が入る。「010」「020」「0120」「0210」などのパーツに分解できる。
- 4 行目以降ではさらに「020」がなくなって、「010」「0120」「0210」に分解できる。さらに次の行のパターンは、それらをひとつ右にスライドしたもの
などが確認できます。要するに $4$ 行目以降では、一度現れた数が右下にシフトしていくだけなので、解けそうですね。
ちょっと気を付けないといけないところとして、「右下にシフト」パターンに入るのに数行かかるのと同様に、列についても左から3列ほどはちょっと微妙ですね。この辺だけ計算していくことになります。
手計算だけで割とすぐに、一歩一歩と考察が進んだこともあって、今回は愚直アルゴリズムの実装を「考察の確認・細部の詰め」や、「実装の確認・デバッグ」等に用いました。しかし、手計算で考察するより前に愚直アルゴリズムを実装してしまっても良かったかもしれませんね。
数分で書ける程度の内容ですし、今回は手計算で一歩一歩進めた考察を一気に3歩4歩進められる可能性を持っていました。多くの問題でどのみちサンプルを増やしたり、デバッグするために役立つので、ロスになることは少ないはず…。
問題F – Sum of Abs
頂点ごとに
- $+B$ のスコアを得る
- $-B$ のスコアを得る
- $-A$ のスコアを得る
のどれかで、ただし
- 辺 $uv$ がある場合に、$+B_u$, $-B_v$ というスコアは両立できない
と言い換えられます。絶対値の和の最大化において、「$+x$, $-x$ を自由に選べる」とした問題での最大化と言い換える典型があります。それの一種と思うと良いかもしれません。連結成分ごとに符号を自由に選べると考えれば、この形になります。
本番はここから、もうひとつ嘘考察をしたあげく、実装が複雑化して答も合わないルートに突き進んでしまいました。(実装に時間がかかり、考察を見直す時間も残せず)
まぁ解説を書いていきます。問題をカットで言い換えます。皆さん、「カット」の定義は言えますか?「フローが流れないようにするための辺集合」ではありませんよ。
カットの定義
ネットワーク $N = (G, S, T)$ があるとします($G$ は有向グラフで辺に容量が定義されており、source $S$ および sink $T$ が固定されている) 。
- カットとは、$G$ の頂点集合の分割 $V(G) = A\amalg B$ であって、$S\in A$, $T\in B$ となるもの。
- 有向辺 $e = \overrightarrow{uv}$ であって、$u\in A, v\in B$ となるものに対する容量の総和を、カットの容量という。
カットを作るとは、各頂点を $A$, $B$ のどちらに入れるかを選ぶことに相当します。「流れないような辺集合」みたいな大域的な(グラフ全体と関係する)見方は必要なく、あくまで頂点ごと選択。カット容量は $2$ 頂点ごとの集計です。
カットによる状態選択の表現
ひとつのものに、$n$ 段階の選択肢を割り当てるときに、次のようなグラフを用いる場合があります。
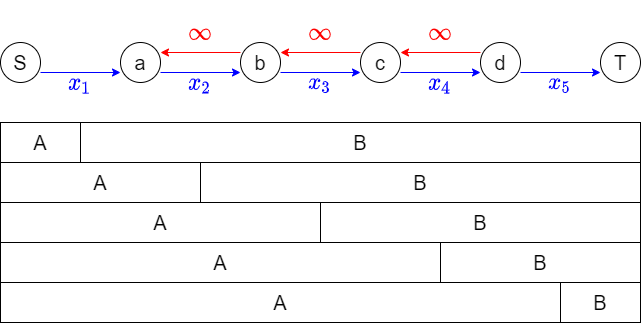
カットとは、頂点 $a, b, c, d$ を集合 $A$, $B$ に振り分けることと対応します。また「容量 $\infty$ の辺」は、最小カットにおいて(可能ならば)選ばれない辺に相当します。例えば上の図で 「$a\in B$, $b \in A$」 という選択は行いたくないという条件を追加しています。
すると、valid な(INF 辺を含まない)カットの作り方は、上の図のように単調に並びます。この図の場合には、ちょうど $5$ つの選択肢を表現していることになります。
「$5$ つの状態があって、それぞれの状態に対する減点が $x_i$ である」というような条件をカットに書き直すことができました。
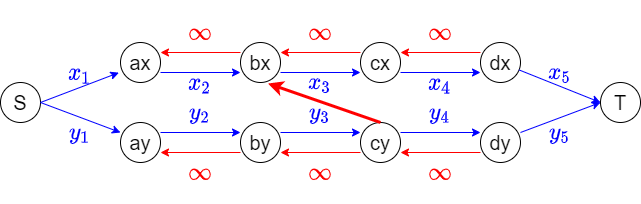
今度は、「$x_1,x_2,x_3,x_4,x_5$ から $1$ つ選ぶ」「$y_1,y_2,y_3,y_4,y_5$ からも $1$ つ選ぶ」ような状況を考えます。これは、先ほど作った形のネットワークを $2$ つ並べればよいです。さらに、適当なところに INF 辺を追加してみましょう。
INF 辺は、valid な状態選択を狭める効果を持っています。上の図だと、「$c_y \in A$ かつ $b_x\in B$」というカットを封印していることになります。「$c_y\in A\implies b_x\in A$」が成り立つようにしているといっても同じです。
$x_i$ の選択と頂点の分割方法の対応を思い出すと、と $x_i$ の選択方法を思い出すと、「$y_4$ または $y_5$ を選ぶならば、$x_3$ または $x_4$ または $x_5$ を選ぶ」というような条件が追加できたことが分かります(適当な容量の辺を使えば、このような選択をしなかった場合の損失を表すこともできる)。
追加できる制約条件の形は限られているので、$n$ 個の選択を $x_1,x_2,x_3,x_4,x_5$ などを並べる際にはネットワークに並べる際には、この点を考慮して状態の並べる順序を調整してあげることになります。
今回の問題
頂点 $u$ に対して、
- $-B_u$ のスコアを得るときの損失:$u_1$
- 壊して $-A_u$ のスコアを得るときの損失:$u_2$
- $+B_u$ のスコアを得るときの損失:$u_3$
とします。ただし、負容量の辺が生じると最大流との対応がつかないので、適当な定数を加えて $u_i\geq 0$ としておきます。損失に書き換えなければならないところにも注意が必要。利得が $x_1, x_2, x_3$ であるとして、$u_i = max\{x_1,x_2,x_3\} – x_i$ とすればよいです。
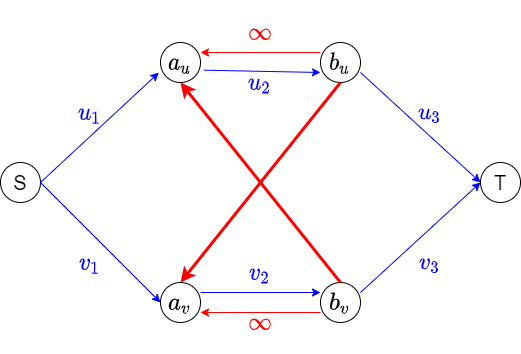
$uv$ が元のグラフで隣接している場合、片方を $+B$, もう一方を $-B$ で使うような選択を禁止ルールに加えます。上のように INF 辺を追加すればよいです。
提出:https://atcoder.jp/contests/arc107/submissions/17763834

