| A | B | C | D | E | F | |
| 問題文 | ■ | ■ | ■ | ■ | ■ | ■ |
| 自分の提出 | ■ | ■ | ■ | ■ | ■ | |
| 結果 | AC | AC | AC | AC | AC |
全体感想
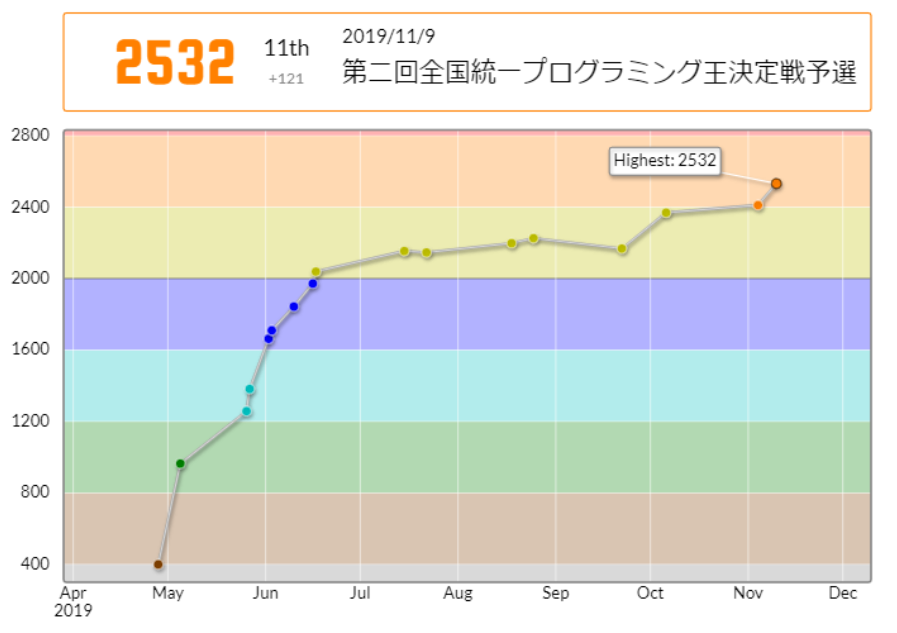
56分5完で、11位でした。そういえば、ratedコンテストでの最高順位です。
橙コーダーとしての初戦。つまり、逆変色チャンスでもありましたが、上手く乗り切れました。特に、WAはまり、バグはまりせずに無駄なくまとめあげられたのが良い出来でした。
問題F。22:25頃に実装を終え、「よし!問題Fも解けた!」と思います。サンプルが合いません。あれ?
問題Fは、誤読しやすい要素があって…(というか自爆?)。「軌跡上のスイッチのON・OFF」が課題となっていますが、交点をダブルカウントしてしまうとダメです…。2つの経路を分解して扱うことができません。
コンテスト開始直後には全ての問題に目を通すのですが、問題Fが行けそうなら行くつもりでした。「行けそうにすら見えなかった」ことが幸いして、一命を取り留めた格好です。一歩間違って解けそうな気分になっていれば、初手で問題Fを仕留めようとして…。やや幸運。
問題B – Counting of Trees
頂点1との距離を見まくっているので、bfs木を思い浮かべます。そもそも木でしたw
深さ $d$ の各頂点に対して、深さ $d-1$ の親を割り当てれば完成です。
これ、木グラフじゃなくても数えられる出来るはずで、その場合はどこかの過去問で、見かけたような…。違いましたっけ?類題がイメージできたので楽でした。
※ bfs木において、辺が現れる位置は、深さが同じ場所・深さが1異なる場所のどちらかであることから数えられる。
また、$D_1 = 0$ は自明な必要条件で、これの確認はコーナーケースとなりうるかもしれません。これも、一度過去問でやらかしたことがあったため、回避できたと思っています。
↓見つかりました、ありがとうございます!ARC044B
問題C – Swaps
いかにも怪しい条件が「$N-2$ 回以下」の部分です。まず、$N-1$ 回のswapを許せば任意の並べ替えができるという常識があります。したがって、「大体任意の並べ替えが作れるな」というところが考察の起点です。もう少しきちんとやってあげると、「$N-2$ 回以下の置換で作れないパターン = 長さ $N$ の巡回置換」に限られることが分かります。
※ 証明に際しては、置換を巡回置換の積に分解したときの、サイクルの個数が良い特徴量を与えます。swap 1回で、$\pm 1$ しか増減しないことがわかります。恒等置換が長さ $1$ の巡回置換 $N$ 個ですので、巡回置換 $1$ 個の状態からは $N-1$ 手以上かかります。逆に、サイクルの個数を必ず 1 つ増やせることから、他の場合は $N-2$ 手以下でできます。
よって、調べたいことは、
・A を並べ替えて項別にB以下にする方法で、長さ $N-1$ の巡回置換以外のものはあるか?
です。これを調べるにあたり、「項別B以下にするための置換はたくさんあるかも」というのが一見ネックになります。とりあえず、置換があるならば 1 つ求めることにします。これには、A,B をソートして、$n$ 番目同士を割り当てる方法があります。この方法で、項別にAがB以下にならないのであれば、どう置換しても無理です(ソート済の添え字で、$B_n$ 以下のものと対にできる $A$ が $n$ 個未満しかないことになるため)。
基礎となる「標準置換」をもとに。この置換が唯一のものでないときには、標準置換から2つの行先を交換できます。すると、どちらかは長さ $N-1$ の巡回置換以外の何かになっているはずなので、必ず $N-2$ 手以下でできます。
問題D – Shortest Path on a Line
まず、辺が多すぎて困るので、削減します。ある区間 $[L,R]$ 内で移動するときには、 $R$ まで移動してしまっても問題ないことが分かります。これが考察の起点となりました。
ある区間は移動先から1度だけ眺めることにすると、あとは1件1件での計算量を抑えることで、全体の計算量を抑えることができます。あとは、$n = 1,2,3,\ldots$ の順に、「$n$ までの最短経路長」を求めていきます。
経路長を dp[n] で表すとします。$n$ に行きつく最後の移動で場合分けをして min をとることで、\[\mathrm{dp}[r] = \min_{l,r,c}\Bigl(c + \Bigl(\min_{l\leq i < r} \mathrm{dp}[i]\Bigr)\Bigr)\] の形の式が作れます。区間 $\min$ を取得する必要があるので、segment木でdpを管理することで、ACを得ます。
問題E – Non-triangular Triplets
とりあえず、cは大きくするほど得なので、「下側 $2N$ 個が $a,b$ で、上側 $N$ 個が $c$ の場合だけ考えればよい」というのはすぐに分かります。
サンプルが少ないですが、とりあえずサンプルを考えます。サンプル2において、無理であることの、筋の良い理由付けを考えます。
・下側:3,4,5,6,7,8 上側:9,10,11
で、下側の和が33, 上側の和が30なので無理です。
何か良さそうな物の見方ができたら、なるべくそれを一般化しようと試みます。今回は、同じ理由で、「$2K \leqq N+1$ が必要であること」が分かります。
等号の場合を考えてみます。私は $(N,K) = (7,4)$ の場合の実験をしました。

この場合、最大値が24です。この周辺から、なるべく規則的に割り当ててみます(A,B,C,D)。そうすると、ちょうどうまいこと残りも割り当てることができました(E,F,G)。
・$N$ が偶数で $K$ がギリギリのとき:真似をすると同様にできます。今回は、$a+b$ よりも $c$ が大きい場合がありえます。

これらの場合よりも $K$ が小さい場合には、ここから全体を定数ずつ引けばOKです。

