| A | B | C | D | E | F | |
| 問題文 | ■ | ■ | ■ | ■ | ■ | ■ |
| 自分の提出 | ■ | ■ | ■ | ■ | ■ | ■ |
| 結果 | AC | AC | AC | AC | AC | AC |
全体感想
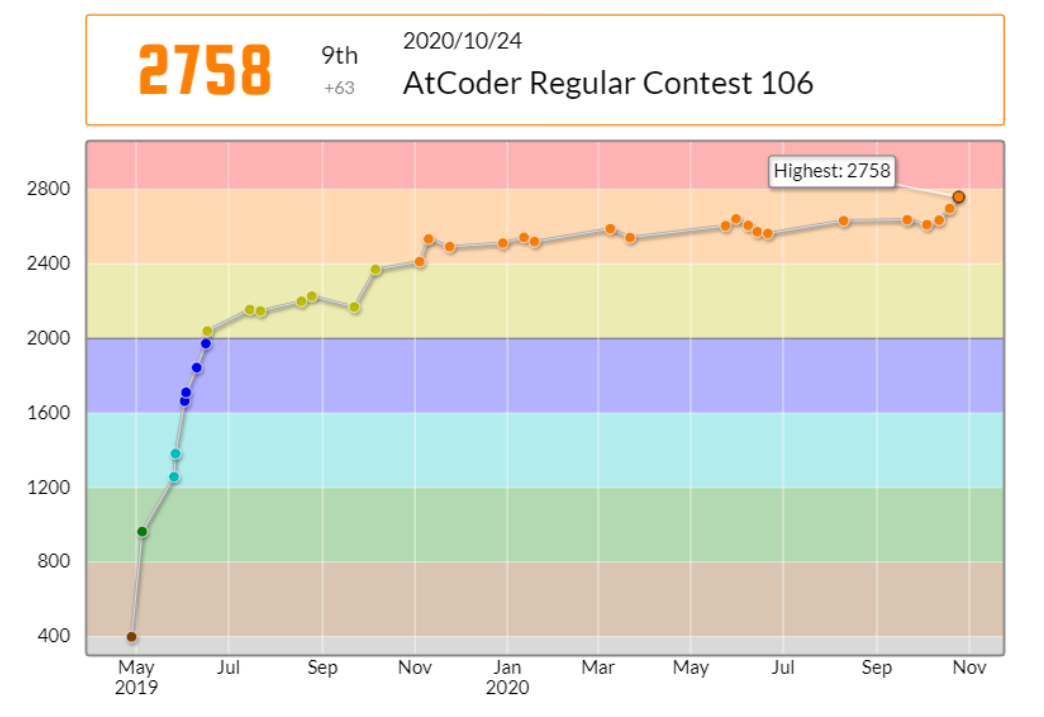
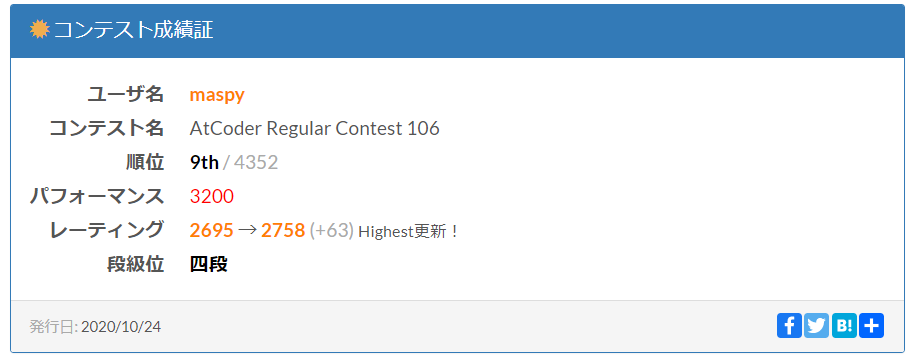
86分 全完 1ペナ、9位 の成績でした。久しぶりの 3200 パフォです。
ARC 級(~2800 rated)での初めての全完(ラス問だけですら時間内に解けたことがなかった)!解ける問題が広がっている実感はあっても、時間内の全完にはなかなか結び付かなかったので、嬉しいです。
早めに 4 完できれば、問題次第で F を優先しようと思っていました。ABCD を解いた時点で 60 分以上残せたこと、F が十分チャンスのある問題に見えたこと、既に F の AC が 4 人出ていたことなどから、これをやってみました。
Hall の定理も、木グラフ数え上げも、春からやっている数学書の勉強会で学んでいたところでしたし、そういう取り組みがプラスに働いているのが分かるのも良いですね。
問題B – Values
ド典型すぎて、ARC で出るのはちょっとびっくりしてしまった(ABC は典型でよくて、ARC は考察重視というコンセプトなので)。
opt さんの記事:https://opt-cp.com/cp/linear-system-incidence/
を貼っておきますか。類題も多くありますね。
自分で考察して見つけられる程度の難易度ではあると思います(グラフと見なしてそれっぽい必要条件を見つけて十分性を証明)。構築が必要なら、全域森をとって、葉から順番に決めていけばよいですね。
問題C – Solutions
区間スケジューリング問題は、貪欲アルゴリズムの代表例として取り上げられることも多く、アリ本でも序盤にも出ているので、ご存知の方も多いのではないでしょうか。
高橋君のアルゴリズムが最適解を与えます。青木君のアルゴリズムは、貪欲アルゴリズムの失敗として有名でしょうか?特に、高橋君のアルゴリズムの最適性を知っていれば、考察を $M \geq 0$ に絞ることが出来てショートカットになります。
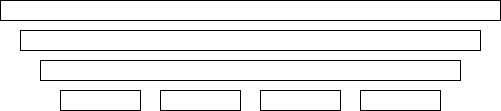
あとはこんな感じでー。極端に青木君が損をする場合を起点に、適当に変形していきます。
問題D – Powers
はじめ、FFT で多重集合 $\{A_L + A_R\}$ を決定する問題かなと思いましたが、$A_i$ が巨大なので違いました。二項定理で展開したらすぐ解けました。
元の式は $L < R$ というような範囲での集計ですが、答は明らかに対称式なので、対称性を使って上手く取り扱うことを考えます。対称な形に表そうとすると、
$$\sum_{i=1}^N\sum_{j=1}^N(A_i+A_j)^X = 2\sum_{i<j} (A_i+A_j) ^ X + \sum_{i=1}^N(A_i+A_i)^X$$
より $\sum_{i=1}^N\sum_{j=1}^N(A_i+A_j)^X$ を求める問題に帰着されます。
二項定理で展開すると、$\sum_{i=1}^N\sum_{j=1}^N f(i)g(j) = \sum f(i)\cdot \sum g(j)$ という式変形が使える形になって勝利です。つまり、$S_i = \sum_{i=1}^N A_i^X$ とおくと、
$$\sum_{i=1}^N\sum_{j=1}^N(A_i+A_j)^X = \sum_{i,j}\sum_{k=0}^X \binom{X}{k}A_i^kA_j^{X-k} = \sum_{k=0}^X\binom{X}{k}\cdot \sum_{i,j}A_i^kA_j^{X-k} = \sum_{k=0}^X\binom{X}{k}S_kS_{X-k}$$ となります。
$S_0, \ldots, S_K$ を前計算しておけばこの式に従って計算するだけです。
計算量改善
$N=K=10^5$ でも解けます。
結局、次の課題をクリアできればよいです。
- $S_n = \sum_{i=1}^N A_i^n$ を、$n=0, 1, \ldots, 2K$ に対して求める
- 各 $0\leq n\leq K$ に対して、$\sum_{k=0}^n \binom{n}{k}S_kS_{n-k}$ を求める
課題 1. は、yukicoder にて既出です:https://yukicoder.me/problems/no/1145
課題 2. は、求めるものを $T_n$ とおくと、$T_n = \sum_{k=0}^n \binom{n}{k}S_kS_{n-k}$ です。このように、二項係数の余分につく畳み込みは、指数型母関数のド典型というやつです。二項係数を階乗で表して両辺を $n!$ で割れば、
$$\frac{T_n}{n!} = \sum_{k=0}^n\frac{S_k}{k!}\cdot \frac{S_{n-k}}{(n-k)!}$$
と書きなおせるので、$f_T(x) = \sum_{n=0}^{\infty}\frac{T_n}{n!}x^n$,$f_S(x) = \sum_{n=0}^{\infty}\frac{S_n}{n!}x^n$ とおけば $f_T = f_S^2$ なので、これも FFT (NTT) で高速に計算できます。
問題E – Medals
ここ半年くらいで、だんだんと Hall の定理 が考察の道具として使えるようになってきましたねー。うれしい。
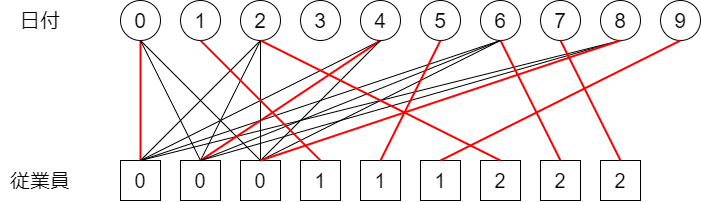
$1$ 対 $K$ の対応を作るわけですが、従業員側は $K$ 個コピー頂点を用意するとして考えました。$NK$ 個の頂点ができます。
このまま Hall の定理を適用しようと思っても、条件が $2^{NK}$ 個あります。Hall の定理はそのまま適用しても、見るべき部分集合が大きすぎることがあって、そういう場合には問題の構造から、調べるべき部分集合を減らしてあげることが必要です。
今回だと、例えば従業員 $0$ に対応するコピー頂点は、$1$ つ選ぶならば全部選んでしまってよいです(近傍の集合は変わらないので、全部選んだ場合の方が単純に条件が厳しい)。今回の制約 $N\leq 18$ が利用できて、$2^N$ 個の部分集合に減ります。
要するに、次の条件に言い換えられます。
$D$ 日間で配り切れるためには、任意の従業員の集合 $S$ に対して、「誰かが出席している日付」の集合 $\Gamma(S)$ の大きさは $KS$ 以上である:$|\Gamma(S)|\leq K|S|$
実はここまではかなり一瞬で考察できたのですが、ここでしばらく止まりました。$\Gamma(S)$ が計算できれば、判定問題が解けて、二分探索で最適解が求まりそうですが…。
ここまでの考察で、ほとんど出席パターン($A$ 日出席し $A$ 日休む)を利用していないので、ここにヒントがあるのかな?というところから考察を進めました。
だいたい 2 日に 1 回は出席していることが分かります。確率 $1/2$ で辺があるってことは、近傍 $\Gamma(S)$、簡単に大きくなるのでは?と。
実際これは正しくて、
- $|S|\geq 1$ のとき、$\Gamma(S)$ は、適当な $1$ 人の出席可能な日付集合よりも大きい
- したがって、$D$ 日目まで見た時点で、$|\Gamma(S)|\geq D/2$
- したがって、$D = 2NK$ 日までみると、必ず $|\Gamma(S)|\geq NK\geq K|S|$
となりました。したがって、高々 $2NK$ 日目までに解があって、$0$ から $2NK$ までの範囲で二分探索をすればよいです。
$D$ を決め打って、$D$ 日間で達成可能であるかの判定問題を解きます。各集合 $S$ に対して、$|\Gamma(S)|$ を計算したいです。
近いものは計算できそうですが、ちょっと足したり引いたりしないといけなさそうです。そういうときは、計算対象や、計算しやすいものをなるべく正確に定式化して、数式を作ります。
- 欲しいもの:$f(S) = \text{count of } \{日付 d\mid ある v\in S が出席可能\}$
- 求められる:集合 $A_d = \{従業員\mid d 日目に出席可能\}$
- 求められる:$g(S) = \text{count of } \{日付 d \mid A_d = S\}$
- $f$ と $g$ の関係式:??
欲しいものと求められるものを書き並べながら考えることが個人的に多いです。
$$f(S) = \text{count of } \{d\mid \exists v\in S, v\in A_d\} = \text{count of } \{d\mid S\cap A_d \neq\emptyset\} =\sum_{S\cap T\neq \emptyset}g(T)$$
と関係式が作れました。
$f(S) = \sum_{S\cap T\neq\emptyset}g(T)$ というのは扱ったことがない計算です。しかし、否定をとった
$\sum_{S\cap T = \emptyset}g(T) = \sum_{T\subset S^c}g(T)$ であれば典型で、高速ゼータ変換により $\Theta(N2^N)$ で計算できます。($S^c$ は $S$ の補集合)この値を $D$ から引けば、$f(S) = |\Gamma(S)|$ の計算が完成です。
問題F – Figures
木グラフの数え上げの問題です。木グラフの数え上げにおいては、
などが有名で、この辺の証明を理解しておくと役に立つのだと思います。特に、頂点にラベルが固定されていて、各頂点の次数が $d_1, d_2, \ldots, d_n$ の場合の木グラフの数え上げは、多項係数 $$\frac{(N-2)!}{(d_1-1)!\cdots(d_n-1)!}$$ で与えられます。
過去問でもあるので、やり込み勢なら知識としてあるかもしれません。
- https://atcoder.jp/contests/cf17-tournament-round3-open/tasks/asaporo2_f
- https://atcoder.jp/contests/NYC2015/tasks/nyc2015_5
文字がかぶるので、問題で与えられている整数列を、$a_1, \ldots, a_n$ とします。次数 $(d_1, \ldots, d_n)$ を固定すると、求める数え上げは、上の木の個数に加えて各部品のうちどの $d_i$ 個を対象にするかの順列をかけて、
$$\frac{(N-2)!}{(d_1-1)!\cdots(d_n-1)!}\cdot \frac{a_1!}{(a_1-d_1)!}\cdots \frac{a_n!}{(a_n-d_n)!}$$
となります。(コンテスト中は、ここで一度愚直解法を書いて、サンプル 3 を確認しました)
さらに、$\frac{a_i!}{(a_i-d_i)!(d_i-1)!} = a_i\binom{a_i-1}{d_i-1}$ と変形できるので、改めて $b_i = a_i – 1$, $e_i = d_i – 1$ とおけば、答は
$$\sum_{e_1+\cdots+e_n = N-2}(N-2)!(a_1\cdots a_n)\binom{b_1}{e_1}\cdots\binom{b_n}{e_n}$$
となります。$(N-2)!(a_1\cdots a_n)$ は $e_i$ によらない定数倍なので、$$\sum_{e_1+\cdots+e_n = N-2}\binom{b_1}{e_1}\cdots\binom{b_n}{e_n}$$ の計算に帰着されますが、これは $f_i = \sum_{n=0}^{\infty}\binom{b_i}{n}x^n$ を用いて $[x^{N-2}]f_1\cdots f_n$ と表せます。$f_i = (1+x)^{b_i}$ より $f_1\cdots f_n = (1+x)^{b_1+\cdots+b_n}$ なので、$$\sum_{e_1+\cdots+e_n = N-2}\binom{b_1}{e_1}\cdots\binom{b_n}{e_n} = \binom{b_1+\cdots+b_n}{N-2}$$ と計算できて、答が求まりました。

