| A | B | C | D | E | F | |
| 問題文 | ■ | ■ | ■ | ■ | ■ | ■ |
| 自分の提出 | ■ | ■ | ■ | ■ | ■ | ■ |
| 結果 | AC | AC | AC | AC | AC | AC |
全体感想
あああ、くだらないミスがなければ優勝できたパターン…。残念。
26 分 2 ペナ → 10位。
問題 F の First AC はとれていたみたいです(問題 F はびっくりするほど簡単だと思った)。
問題F、4:35 で初提出したんですけどWA。「return X >= 0」を「return 1 * (X >= 0)」に変えれば通るやつ。しかも X は 0 以上が保証できるので「return 1」でもよい。
bool 値と int の計算が絡むと適当にキャストされるのでこうしてしまったんですが、この値がその後計算されずに出力されてしまう場合があって。正しい答に紛れてたまに「True」が出力されてしまっていました。とりあえず、自身のバグらせメモに追加します。
6 分 + 2 ペナ を失ってしまい、1 位とれるペースで解けたのが 10 位という結果になってしまった。まぁ、rated じゃないときにレアなミスを引けて、その分上達できたので、良かったです。
問題E – Akari
H, W が巨大でグリッド全体をメモリに置けないと実装量が増えてしんどい思いをすることになりますが、その必要はなかったです。
各電灯から、一方向。例えば下にのみ光が発せられる問題を解きます。これを 4 方向について解いてマージすればよいです。
下方向にのみ光が発せられる場合には、上の行から順にループしていけば簡単に解けます。$4$ 方向分計算するのが面倒ですが、$90$ 度回転して実装をまとめる簡単というテクニックを使用しました。
res = np.zeros((H, W), np.bool_) # 光ったマス
for _ in range(4):
res, G = res.T[::-1], G.T[::-1]
# 下方向に解く
A = np.zeros_like(res)
H, W = A.shape
for h in range(H):
if h >= 1:
A[h] |= A[h - 1]
A[h][G[h] == 1] = 1
A[h][G[h] == -1] = 0
res |= A提出コード(https://atcoder.jp/contests/abc182/submissions/17968851)より。
G に、グリッドの情報が入っています。(電灯を 1、ブロックを -1 とした (H,W) の 2 次元配列)。自身を含む下方向に光を発するとして解いて、解いた結果が A に入るようにします。$4$ 方向それぞれの結果をマージして、全方向の集計 res を得ています。
for _ in range(4):
res, G = res.T[::-1], G.T[::-1]ここの部分が、$90$ 度回転と呼ばれる実装です。計算前のグリッド、計算結果をマージする先ともに $90$ 度回転しています。これを $4$ 回行いながら、あとは「下方向」の実装に専念すれば、$4$ 方向分の実装ができたことになります。
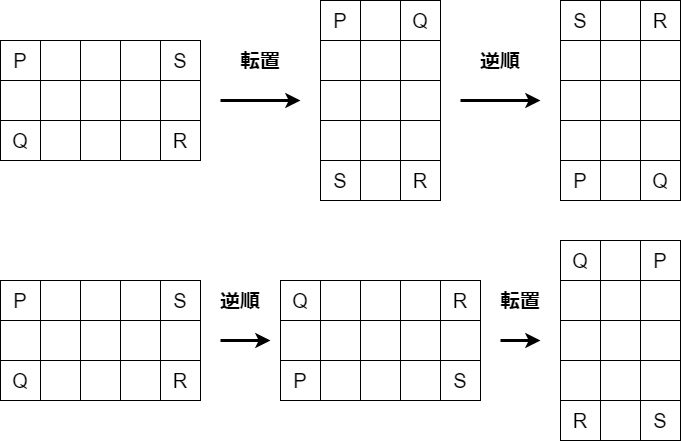
転置と逆転を適当な順序で $1$ 回ずつ行えば、適当な方向に $90$ 度回転されます。なお、逆順をとるのは行方向でも列方向でも構いません。回転方向を制御したい場合には四隅の移動を考えますが、単に $4$ 方向の処理をまとめたいだけであれば、「A.T[::-1]」でも「A[::-1].T」でも「A[:,::-1].T」でも、転置と逆転を 1 度ずつ行えばよいので、覚えることや考えることがかなり少なくて済みます。
なお、numpy.ndarray のこの手の操作は、配列のコピーを行わず同じメモリ領域の参照方法のみを変える(view をかえす)ため、配列が巨大であっても定数時間です。
問題F – Valid payments
例えば硬貨が 1, 5, 10 円であるとします。
例えば $123$ 円を支払うとして、支払う $1$ 円玉の個数で場合分けをします。$3$ 枚または $0$ 枚です。答を $f(123, [1,5,10])$ のように書けば、$$f(123, [1, 5, 10]) = f(120, [5, 10]) + f(125, [5, 10])$$ のような式が得られます。あとはこれをメモ化再帰に乗せれば実装が終わりです。$f(120,[5,10]) = f(24, [1,2])$ などの変形は、してもしなくてもどちらでもよいと思います(私はしませんでした)。
もともと最小の硬貨を支払うパターンのない場合もある:$f(120, [1, 5, 10]) = f(120, [5, 10])$ など。にも注意しましょう。
この手の考察は、通常「桁 dp」と呼ばれることが多いと思います。基本的な桁 dp はすべて(多分?)、「$1$ の位で場合分け → 再帰」の形で考えることができて、私の ABC 解説でも何度か取り上げています。
メモ化再帰はかなりお手軽実装で、64 bit 整数範囲を相手にするだけならかなり推奨できると思います。$10000$ 桁の整数など、巨大な計算を扱う場合には、巨大な整数をキャッシュすることを避ける・深い再帰を避ける / などの目的で、配列とループの形で書くのが望ましい場合もあります。今回の問題なら、
- 左から $N$ 桁分を見たとき、$X$ 円を支払う方法 / $X+1$ 円を支払う方法
のように、$2$ つの値を持って更新していく形になります(私の考察手順だと、よく知られた(?)桁 dp の状態の持たせ方と少し異なる場合分けになっているようですが、今まで問題が起きたことはありません)。

