| A | B | C | D | E | F | |
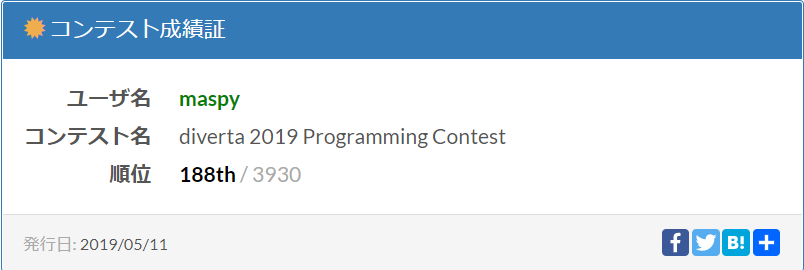
| 問題文 | ■ | ■ | ■ | ■ | ■ | ■ |
| 自分の提出 | ■ | ■ | ■ | ■ | ■ | |
| 結果 | AC | AC | AC | AC | TLE |
全体感想
ABCDとEFで、かなり難易度差の大きな問題セットでした。このようなセットでは、EFのどちらかを正解しきるか、ABCDを1分でも速く仕上げるかのどちらかをしないと順位は振るわないようです。なるほどな、そりゃそうか。
Eは1時間くらい考えて、ようやく計算量を減らす方法に気が付きました。遅延評価dpというのは私は初めてのアイデアでした。せっかくのアイデアだったので点数に結びつけたかったですが、コンテスト中に正解しきれず…無念。
AtCoderサイトが尋常ではなく重い日で、コードテストも思うように出来ませんでした。ここがまともなら正解できたはずなのですが…言い訳っぽいw
問題C – AB Substrings
すぐに分かったけど、変なコーナーケースがないのか厳密に証明を埋めるところにやや時間をかける。そこに5分かけるくらいなら、コンテスト的にはさっさと投げてみる方が良いのでしょうねw
問題D – DivRem Number
$N = mx + x$かつ$x < m$。$x+1 = m$まわりの処理ミス回避を丁寧に。
手元で$N\leq 100$についてナイーブな実装と比較して答確認。
問題E – XOR Partitioning
急に難易度が上がる。全然分からない。
しばらくして、累積和の意味で $(0,x,0,x,\ldots)$ となる場合を数える問題に言い換える。
全体の累積和が $0$ でない場合が難しい。$x$ が固定されているならば、左から順に見ていって $0$ または $x$ が出てきたタイミングで、$(0,x,\ldots,0,x,0)$ 型の部分列の個数と $(0,x,0,x,\ldots,0,x)$ 型の部分列の個数を更新する dp が簡単につくれる。$x$ が出てきたタイミングだけ更新するのであれば、数列の項1つ1つに対して1項更新するだけなので、 $x$ が何種類あろうが $O(N)$ で解ける。しかしこのままだと、 $0$ が出てきたタイミングであらゆる $x$ に対して更新しなければならず、worst caseでの計算量が爆発してしまう。
数列全体の累積和(xor sum)が $0$ でないならば、 $x$ の候補が一意に定まるので簡単だ。しかし問題文を読み返すも、やはりこの辺のworst caseに対処する必要がある。
考え方を変える。$0$ が出てきたタイミングで、「 $0$ が出てきたよ」というflagのみ更新するくらいしかやってはいけないだろう。すると、 $0$ が出てきた回数だけ覚えておいて、 $x$ が出てきたタイミングでそれをまとめて処理するという遅延評価 dp を思いつく。
これでも、$0$ が出てきた回数 $n$ 回に対して計算量 $n$ が必要なら同じことだ。dp の更新をよく考えると、線形な関係式なので、$x$ によらない行列をかける操作で表せる。その行列の $n$ 乗をかけるわけだが、当然毎回 $n$ 乗計算しなくても、行列のべき乗を事前計算しておけば良さそう。
具体的に式に表わしてみると、件の行列は $\pmat{1&1\\0&1}$ だったので、$n$ 乗は事前計算するまでもなく $\pmat{1&n\\0&1}$ に等しかったです。
コンテスト中には整理し切れず。コンテスト後にACしたコード:■。

