| A | B | C | D | E | F | |
| 問題文 | ■ | ■ | ■ | ■ | ■ | ■ |
| 自分の提出 | ■ | ■ | ■ | ■ | ||
| 結果 | AC | AC | AC | AC |
全体感想
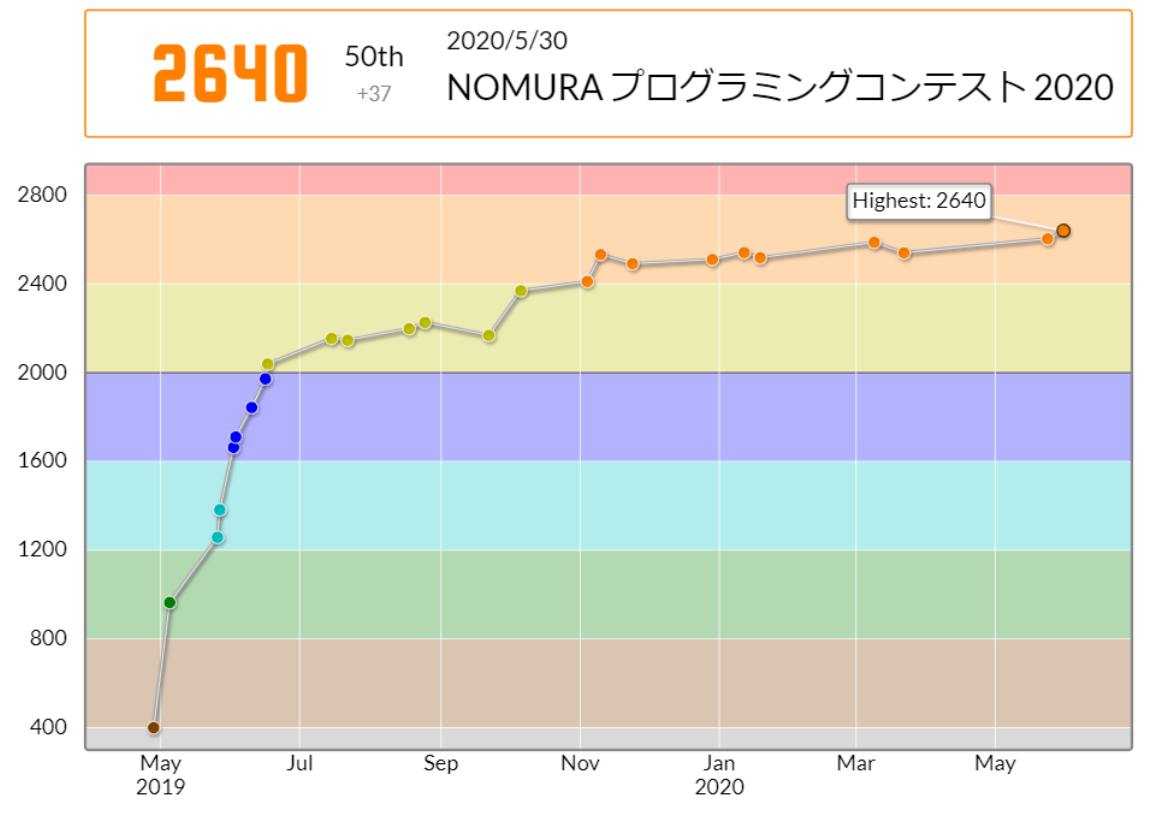
ABCEの76分4完 + 2ペナ。4問しか解けなかったわりにはDではなくEを選択したこと、ABCEパターンの中ではタイムが良かったことから、赤パフォをとることができました。
偏りもあると思いますが、最近、赤パフォがそれほど難しくないと少し感じられるようになってきました。とか言ってたら思うようにパフォが出ない回を引きそうですけど…。
とりあえずCを解いたあと、D~Fを眺めます。Dを10分くらい考えてあまり進展しなかったので、Eを先に取り組みました。Eを撃破時点でのこり44分。Dに挑んで解けたとしても時間ギリギリになりそう(Fを解くのは絶望的)だとか、4完最遅と5完最速だとそれほど順位が変わらないなども考慮して、最後はFだけを考えていました。
コンテスト時間内にFの解法の大筋は見出せたのですが、細部の式をきちんと詰めて実装する時間は残っておらず、解ききれなかった、残念。
そろそろARC級のラストにもある程度の勝率はあると思うのですが、過去 10 回(?)の参加で一度もコンテスト中の正答は至っていません。あと少し時間があれば…というところ止まり。まだまだ赤上位~の方とはかなり差を感じてしまいますね、頑張ります。
問題D – Urban Planning
コンテストの2日後に解きました(提出:■)。
重要ワードをtwitterで見かけてしまっていたこともありスムーズに解けました。考察の最難所を超えればわりと単純で、考察ステップ数は少ないですが、それでも結構難しい問題に感じました。
コンテスト本番で考えたこと:
・要請を固定すると、道を作る個数は簡単(要請に辺を貼って連結成分を数える)。
・デフォルトの要請を確定させてしまうと、その時点での連結成分は2種類ある:「唯一のループを持ち、未確定の要請がない」「木グラフで、未確定の要請がひとつある」
・それらの成分の構造はどうでもよくて、頂点数と未確定の要請の有無だけが大事。
各連結成分から 1 本ずつ辺を決めていったときに、最終的にできる連結成分の個数がどうなるかを調べると良さそうです。一応、連結成分の個数ごとに「何通り」が計算できる必要はなくて、その和が求められれば良いことも確認しておきます。
ここで、次の類例を思い出しました:
・長さ $N$ の順列 $N!$ 通りのうち、サイクルが $k$ 個できるようなものの個数 $c(N,k)$ を求めよ
これは第一種スターリング数とよばれる典型的な数え上げのひとつで、順列を有向グラフとして表したときに、「最後の元を除いた状態」で場合分けをすることで、dpの漸化式を作ることができます。($1, 2, …, n+1$ から $n+1$ を「除く」と、サイクルの個数が不変(たいてい)またはひとつ減る($n+1$ が不動点)ことから漸化式ができる)。

この手の問題とめちゃくちゃ似ているように見えたので、そこから考えようとしましたが、10分ほど考えて上手くいかず(本番ではここで問題Eに切り替えました)。順列だと「最後の元を除いた状態」が綺麗に定義できるんですが、写像だとこういう扱いは難しいのでしょうか?
(コンテスト後)
すべての要請を書き込むと、今回のグラフは全ての頂点の出次数が $1$ になります(functional graph)。あるいは無向グラフとしては、連結成分の頂点の個数 $v$ と辺の個数 $e$ が $v = e$ を満たします。木グラフにひとつ辺を付け加えた形をしていて、唯一(unique) のサイクルを持ちます(unicyclic graph)。したがって、連結成分を数えることとサイクルの個数を数えることは同値です。
$v = e$ となるグラフの唯一のサイクルに注目する議論は過去問でも珍しくないですが、「連結成分の個数」を「サイクルの個数」に置き換えるというのは初めて見たかもしれません。前者の方が調べやすい性質に見えてしまいかねないですが、今回の問題設定では連結成分よりもサイクルの方が確かに扱いやすく、ここを超えたら解くのは比較的易しいです。
問題は、あらゆる要請の定め方に対して、サイクルの個数を足し合わせることです。これを、サイクルの寄与ごとに分割します。
デフォルトの要請を定めた時点で、すでにサイクルを作っている成分については、その成分を含む新たなサイクルを作ってしまうことはないので、考察から除外します。すると、以下の問題が解けると良さそうです。
頂点数 $n_1,n_2,\ldots,n_k$ の有向根付き木がある。これらの根からひとつずつ(自己ループでない)有向辺を貼る。このような操作を全種類やったとき、どのようなサイクルが何回現れるかを調べよ。
サイクルは、いくつかの有向根付き木の間をわたり、自身に戻ってきます。そこで、どの有向根付き木をどのような順に移動するかで分類してみます。以降、下の図の場合に計算を考えていきます。(大きさ 3, 2, 4, 2 の根付き木)
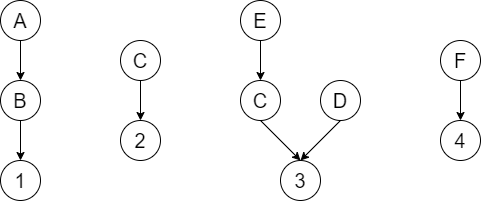
例えば上の図(根を 1, 2, 3, 4 とする有向根付き木がある)において、根を「1 → 2 → 3 → 1」の順にまわるサイクルを考えます。このサイクルにはいくつかの種類(1→2→3→1 以外にも、 1→C→2→D→3→A→B→1など)がありますが、$1$の移り先を $2,C$ のどれにするか、$2$ の移り先を$3, C, D, E$ のどれにするか、$3$ の移り先を $1, A, B$ のどれにするかを決めることで定まり、$4\cdot 3\cdot 2 = 24$ 通りのサイクルがあります。順序を固定せず、「単にこれら $3$ つの根付き木をまわるサイクル」というだけであればその $2!$ 倍です(1→2→3→1 と 1→3→2→1)。したがって根の集合 $\{1,2,3\}$ からは $48$ 通りのサイクルが作られます。
「すべての要請の定め方に対する、これらのサイクルの登場回数の合計」でいうと、頂点 $4$ の行先を自由に決められることから、$10$ 回ずつ現れます。$48 \cdot 10$ とかを足すことになりますね。
$\{1,2\}$ であれば、$3\cdot 2\cdot 1! \times 10^2$ といった要領ですね。
結局、根付き有向木の各部分集合に対して、大きさの積をとったあと、階乗とか $(N-1)^n$ みたいなのを掛け合わせて集計すればよいことになります。掛け合わせる係数は、部分集合の大きさだけから定まるので、部分集合の大きさごとに集計しましょう。
部分木の大きさを $a_1,a_2,\ldots,a_k$ として、その基本対称式を一通り計算すればよいです。これは、$\prod_i (x + a_i)$ の係数です。
最後に、ひとつの有向根付き木だけで完結するサイクルだけ注意が必要で、上の式だと根が自身にうつる場合も含めてしまう可能性があるので、そこを補正すれば完成です。
問題E – Binary Programming
とりあえずサンプルを合わせます。空文字列から挿入していってもよいのですが、作成途中の文字列とゴールの文字列が比べにくく感じたので、ゴールの文字列から 1 文字ずつ除いていく方針で考えました。
気づきとして、$0$ が残っている限りは、$0$ のどれかを除くべきだということが分かります。$1$ を除く操作は、左右どちらかの最寄りの $0$ を除く操作と比べたら完全下位互換だからです。これでかなり考えやすくなりました。

とりあえず、サンプル 2 の操作を適当に可視化してみます。この場合だと、$0$ を除き終わるまでに、$14$ 点を得られていることが分かります。
操作列の合計得点を観察するにあたり、ひとまず「それぞれの「1」ごとに点数を見る」「それぞれの「場所」ごとに点数を見る」という 2 つの視点は思い浮かべます。そうしながら、操作順による得点の差異を見ようと考えていたところ、特に「1」ごとの点数について次のような気づきを得ました。
- 右端の「1」の得るスコアは操作順に影響されない
- 偶数個並んだ「1」の得るスコア合計は操作順に影響されない
「1」ごとに焦点を当てて、このサンプルの場合の操作列を比較すれば、わりと気づきやすい性質だと思います。またこのサンプルは、これらの性質を気づくのには向いているものの、より進んだ考察にはちょっと不向きな感じがしました。ので、乱数で自作した適当な列を元により考察をすすめていきます。偶数個ならぶ「1」の部分は無視できることもあって、「1」が連続しないものを書いてみます。

適当なひとつの「1」に注目して、どう動くかを考えると、左右どちらの「0」が削除されるかにしたがって「左へ移動」の回数と「足踏み」の回数が定まっていると分かります。したがってスコア最大化にあたっては、「奇数マスで足踏みする回数」だけが重要だと分かります。(足踏みがなければ奇数マスに居られる回数は定数)(この辺は「サンプル 2 」で右端の「1」は操作順の影響を受けないことを見つけていたのも、発想として役に立ったと思います。)
左への移動は得しているのか損しているのか分からず、いつ移動すべきか悩ましいのが本問での第一印象でしたが、奇数マスで足踏みできるかだけが重要だとなってくると、考察は一気に易しくなります。ある「1」が偶数マスに居るときには、右側の「0」を削除しないにこしたことはないわけですが、ここまで分かれば最適な操作列はすぐに見つかります。
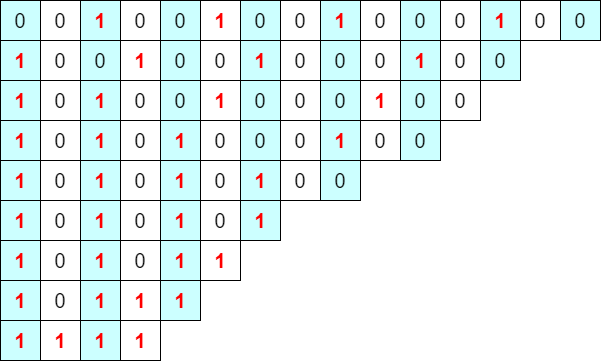
連続する「1」を除いておいた(間にひとつ以上「0」がはさまっている)おかげもあって、左の方にある「1」から順に奇数マスに持ってくるだけで、偶数マスで足踏みしない操作列が実現できます。あとはスコアを計算すれば終わりで、難しくはないです。
実装は、「1」が $k$ 個まとめて並ぶ部分をまとめて計算しました。足踏みを始点から終点までの移動のうちの好きな場所で消化できることから、スコアが計算できます。
問題F – Sorting Game
コンテストでは、ラスト40分間をこの問題にあてました(解ききれず)。
結果的には、考えるべき点を順に考えていけば、比較的ふつうな考察の積み重ねで解ききれる問題で、そんなに難しくなかったです。しかし、短時間で確実に解ききるにはまだまだ実力不足でした、残念。
まず、ソート可能性について考えます。「この2つはswap可能」「この2つはswap不可能」という条件が指定されていて、swapによるソートが可能かを問われているのですから、これは
- $i<j, a_i>a_j$ ならば $a_i$ と $a_j$ はスワップ可能(1bitだけ異なる)
と進むのが自然でした(本番中は、「swap不可能なもの同士に制限すると昇順」という中途半端な必要条件に注目してしまい、かなりタイムロスしてしまいました)。
「任意に bit を消したときに~」という条件についても、
- $i < j$ となる任意の $a_i,a_j$ は次を満たす:任意の $s$ に対して $b_i = a_i \& s$, $b_j = a_j \& s$ とおくと、$b_i \leq b_j$ または 1 bit違い
という形で盛り込めます。よってこの $(a_i,a_j)$ の条件を整理するのが次の課題です。
$x=a_i$, $y = a_j$ としまして、$k$ bit 目を $x_k$, $y_k$ などと書いてみます。2 進法と不等式の関係が問題なので、最上位の bit から順に考えていきます。最上位 bit が $x_k < y_k$ を満たすならば、その bit が残る場合の条件は自明になるので、その bit が消える場合だけを考えればよいです。したがって、$k-1$ 番目までの bit が条件を満たすかという問題になります。$x_k = y_k$ のときも同様です。$x_k > y_k$ ならば、下位の bit は全て等しいことと同値です(ひとつも bit を消さなかったときを考えると必要性が分かり、十分性も容易。)
以上を踏まえると、最上位 bit の状況を固定すると、下位 bit について解くべき問題の形が明らかになって、再帰的に問題を解くことができそうです。例えば、最上位 bit を次のように並べたとしましょう。

左から順に見て、$(1,0)$ となっているところの下位ビットは、以降等しくなければいけません。すると、下位 bit についてはある区間が等しくならなければならないことが分かります。
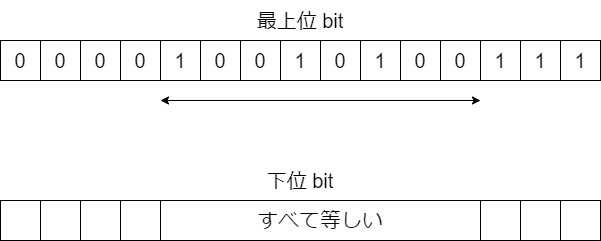
より具体的には、左端の「1」と右端の「0」ではさまれる区間のところは、下位 bit が定数列である必要があります。それ以外には、下位 bit だけで見ても条件を満たすことが要請されます。定数列であることが強制される部分を 1 項と見なしても条件は保たれるので、問題を解くための再帰的な構造が見つかりました。
$(M,N)$ に対する数え上げの「答」を$f(M,N)$ とします。上の例では、$(M,N) = (15,N)$ の問題において、最上位 bit が 000010010100111 であるようなものの数え上げは、$f(8, N-1)$ に等しいことを示しています。いろいろな最上位 bit を考えて集計することで、$f(M,N)$ をいろいろな $f(k, N-1)$ の和として表せるため、dp計算できます。(本番、この辺まで考えたところでタイムアップでした)
これを下手に書くと計算量が $\Theta(M^2N)$ になってしまうので、あとは $1$ 次元分高速化できれば完成です。
小さい $M$ について遷移を書いてみます。遷移は $N$ に依存しません。適当な $N$ に対して $f(k, N-1)$ の値を $a_k$, $f(k, N)$ の値を $b_k$ としてみます。
$$\begin{align*} b_1 &= 2a_1, \\ b_2 &= a_1 + 3a_2, \\ b_3 &= 2a_1 + 2a_2 + 4a_3, \\ b_4 &= 4a_1 + 4a_2 + 3a_3 + 5a_4, \\ b_5 &= 8a_1 + 8a_2 + 6a_3 + 4a_4 + 6a_5,\\ b_6 &= 16a_1 + 16a_2 + 12 a_3 + 8a_4 + 5a_5 + 7a_6, \\ \vdots \end{align*}$$
大雑把には $b_k$ のうち $a_i$ から遷移するの、定数列が強制される区間の長さが $k – i+1$ の場合です。区間をどこに設定するかで $i$ 倍、区間を固定したあと適当な $2$ べきがかかって、$i\cdot 2^{k-i-1}$ が典型的な係数です。定数列が強制される場所がない場合(最上位が 000001111 みたいな場合)として、$a_k$ の係数が少し異なる規則で入っています。
あとはこれを適当に高速化します。私は $\frac{b_k}{2^k}$ が適当な累積和で書けることを使いましたが、今見返すと、$b_k$ を $2b_{k-1}$ から計算するような書き方の方が易しかったですね。

