| A | B | C | D | E | F | |
| 問題文 | ■ | ■ | ■ | ■ | ■ | ■ |
| 自分の提出 | ■ | ■ | ||||
| 結果 | AC | WA |
全体感想
連続 rated の 3 回目!初の 1200+ ratedでした。
結果として、1完。いやーダメでした。問題AはAGC-Aの中では最難に感じてびっくりしました。問題B、問題Cもこの位置の問題としては難しめ…とはいえ、十分過去問で練習できている難易度帯だったので、ここで2敗してしまうのは情けないところです。
問題Aを解き終わるのに 30 分、これは、10分で大体方針が立ったあと、問題BやCも少し考えていたのでAに専念していたら15~20分だったと思うのですが、この時は問題Aのタイムがパフォーマンスに影響する(1完で終わってしまう)可能性は全く考えておらず…。
問題Bが一番ひどかったですね。考察の確度の低いまま進んでしまい、間違いに気づいたあとも無理やりな修正を試みようとして1時間以上を消し飛ばしました。AGC-Bが絶対に簡単に解ける、解けなきゃいけないレベル帯だという気持ちもマイナスに働いたかもしれません(早めに C に切り替えた方が良かった)。
最後の45分を問題Cにあてたのですが、こちらは時間内にほとんど正しいところまでいけていました。1箇所実装ミスがあって、結果的にはあと10分あればという感じです。
問題ABCの中では問題Cが最も典型度が高いことには割と序盤で気づいていたのに、ここに使える時間が少なくなって解けず終いとか、いろいろ下手でした。
問題A – Xor Battle
非負整数 $0, 1, \ldots, 2^{60}-1$ は xor に関して $\F_2$ ベクトル空間をなし、その構造は $\F_2^{60}$ と同型です。よって以下では,$A_i \in \F_2^{60}$ と見なします。
ゲームの必勝に関する考察では、何はともあれゲームの終局付近から考察を進めるのが基本です。例えば最初の1手の戦略を決定するには以降のいろいろな展開を気にしないといけませんが、最後の1手の戦略は明らかに決まります。
(後の都合により)$A_i$ に $0$ も許すことにしておきます。
- 最後の手番が $0$ のとき:手番に回ってきたときに、$0$ または $A_N$ であれば勝ち。
- 最後の手番が $1$ のとき:$A_N\neq 0$ であれば勝ち。
となります。最後の手番が $1$ のときには簡単で、そうでないときには、「$0$ または $A_N$ を作ることが目標のゲーム」として再帰的な構造が見つかります。「$0$ または $A_N$ を作る」は、剰余空間を考えると「$0$ を作る」に取り換えることができます。結局次の形になります。
$\F_2$ ベクトル空間 $V$ と、$V$ の元の列 $A_1,\ldots,A_N$、文字列 $S$ に対するゲームとして一般化して考える。このゲームを $(V, [A_1,\ldots,A_N], [S_1,\ldots,S_N])$ と表すことにする。このゲームの勝敗は
- $S_N=1$ かつ $A_N \neq 0$ ならば人 $1$ の勝ち.
- $S_N=1$ かつ $A_N = 0$ ならば、ゲームの勝敗は $(V, [A_1,\ldots,A_{N-1}], [S_1,\ldots,S_{N-1}])$ の場合と等しい.
- $S_N=0$ のとき、部分空間 $W = \{0, A_N\}$ による剰余空間 $V’ = V/W$ を考える。$v\in V$ の $V\longrightarrow V’$ による像を $v’$ とすると、ゲームの勝敗は $(V’, [A_1′, \ldots, A_{N-1}’], [S_1, \ldots, S_{N-1}])$ の場合と等しい.
と再帰的な構造で計算することができます。あとはこれを実装すればよいです。
いろいろな元を $V’=V/W$ ($W=\{0, w\}, w=A_N$)にうつすところが問題となります。$w = 0$ は自明です。
$w\neq 0$とします。$V = W\oplus W’$ となる補空間 $W’$ に対して $W’\cong V’$ となるので、$W’$ にうつす形で実装します。$w$ の $k$ 番目の成分が $1$ であれば、$k$ 番目の成分が $0$ であるようなベクトル全体を $W’$ ととれます。写像 $v\longmapsto v’$ は、$k$ 番目の成分があるか否かに応じて $v’ = v’-w$ または $v’$ となります。
対応する bit 演算として、$k$ として $w$ の最上位ビットをとった場合、$v’ = \min(v’, v \xor w)$ と書けて簡潔のようです(みたいなことがコンテスト後話題になっていたと思います)。
問題B – 01 Unbalanced
区間集計を累積和の形にすると、次の問題にはなります。
- 「-1, ?, 1」の 3 種が並んだ文字列がある。
- ? を $\pm 1$ のどちらかに置き換える。累積和の最大値と最小値の差を小さくせよ。
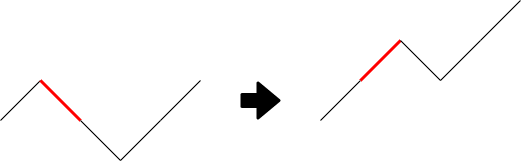
こんな絵を描きながら考えていました。

累積和の折れ線グラフで、傾きが指定されている場所と未定の場所があって、折れ線をなるべく少ない上下幅に収める問題です。
(しばらく本番中の失敗考察なので、解法だけ確認したい人は飛ばして)
結局問題になるのは最小値と最大値をとる部分だけなので、まずは最小値をとる位置を固定し、最適解の構造を考察しました。一度最小値をとったら、そこから右側は貪欲に決める(最小値を下回ることがない範囲で辞書順に $-1$ を優先して選択する)のが良さそうだと分かります。実際 $\ldots, 1, \ldots, -1$ を $\ldots, -1, \ldots, 1$ に交換する議論を考えると、早い時刻に $-1$ を優先して困るのは途中で最小値を更新してしまう場合に限ることが分かります。
【本番はここで嘘考察をしました】初めて最小値をとる部分の手前の選択に注目する。もしここに $-1$ があれば、それを $+1$ に変えると最小値が増えるので、損をしない。よって最適解の構造として、最小値に到達するまでは $+1$ を選び続けることを仮定できる → 嘘で。$-1$ を $+1$ に取り換えると、確かに最小値は増えるのだが、最小値が $1$ しか増えずに最大値が $2$ 増えるケースがあって、損になることもある。
嘘考察にもとづいて、将来的に最小値を減らす可能性がある選択肢は避けるような貪欲解法を実装してしまったのですが、当然WA(この時点で 50 分も使ってしまい…)。上のような反例(最小値を改善しても最大値で損する場合)があることに気づいたあと、小手先のソースコード書き換えで対応したものの、ダメでした。遅いのはともかく、考察の正確さには気を付けているのですが、失敗。かなしい。
コンテスト終了後に考えて解いた方針です。(解説でいう「二分探索を用いた素朴な解法」にあたると思います)
まず、次の判定問題を考えます:
(問題1)最小値 $m$ 以上、最大値 $m+n$ 以下を実現できる。
これは易しいです。常に $[m,m+n]$ の範囲を動くようにすればよいのですが、各時点で到達できる座標の集合の情報をもって dp すればよさそうです。座標を全部持とうとすると $\Theta(Nn)$ の計算量になりそうですが、到達可能な座標全体がおおよそ連番になる(正確には、偶数・奇数の中で連番)になることから、最小値と最大値の $2$ 値だけを持って更新していくことで、$\Theta(N)$ で問題1の判定が行えます。
これだと問題の答を二分探索するには至らないです。実際に判定したいのは次です。
(問題2)ある $m$ に対して最小値 $m$ 以上、最大値 $m+n$ 以下を実現できる。
これを色々な $m$ に対して個別に計算しようとすると上手くいきませんが、「初期位置 $0$、$[m,m+n]$ におさめられるか判定する問題」は「初期位置 $-m$、$[0,n]$ におさめられるか判定する問題」と書き換えることができます。よって、これは次の問題と同じです。
(問題3)$0$ 以上 $n$ 以下の任意の初期値から出発して、最小値 $0$ 以上、最大値 $n$ 以下を実現できる。
これは問題1のような dp をすればよくて、判定問題を計算量 $\Theta(N)$ で解くことができます。「偶奇ごとに連番」なので、出発位置が偶数の場合、奇数の場合に分けて $2$ 回計算することで解きました。(コンテスト後提出:■)
問題C – Range Set
大体、公式解説と同じですが、dp の作り方は少し違うっぽい?です。
まず、判定問題を考えます。つまり、操作後の文字列が与えられたとき、それが操作で作れるかを調べます。
もとの数と関係なしに上から上書きしていく系の操作では、操作の逆順に考える手法が有力で、過去問でも複数の例があります(例:https://atcoder.jp/contests/cpsco2019-s3/tasks/cpsco2019_s3_d)。
例えば $A=3, B=6$ として、「00110001001」に対する判定問題を考えます。それっぽい「000」がひとつあります。(この例はともかく)一般には「000」があってもそこを操作対象としているとは限らないですが、そうでない場合も操作を 1 回追加することで、注目している「000」は最終手に操作対象となったとしてよいです。
「000」と塗りつぶす操作をひとつ遡ることは、「00110001001 ← 0011***1001」のように、ワイルドカードに置き換えることと対応します。すると「11***1」の部分が 111111 である場合もこの形なので、「00110001001 ← 0011***1001 ← 00******001」のように、ワイルドカード地帯を拡大できます。「0**」「*****1」などを使えばこれを全域に広げることができて、「00110001001」に対する判定問題が解けました(作れることが分かった)。
$A$, $B$ に順序を入れて、$A \leq B$ であるとします。一度長さ $B$ のワイルドカート地帯ができれば勝ち確だと分かります。したがって、「$1$」が $B$ 個続く場所があれば勝ちです。そのような場所が見つかるまでは、ひたすら「$0$ が $A$ 個続く場所」のワイルドカード化を行っていきます。などと考えていくと、結局問題の文字列は次と同値です($A < B$ とします):
$0$ が $A$ 個以上つづく部分を全て $1$ に取り換えたときに、$1$ が $B$ 個以上続く部分がある。
余事象をとることで、次を数える問題を解けばよいです。
$0$ が $A$ 個以上つづく部分を全て $1$ に取り換えても、$1$ は $B-1$ 個以下しか続かない。
あとはこれを dp で計算するだけです。本番では、この辺で残り 25 分程度でした。
「何文字目まで作ったとき」「$0$ がいくつ続いているか」「その $0$ が $1$ 化されたとした場合、$1$ がいくつ続くことになるか」あたりを状態としてあげることを考えますが、状態数が $\Theta(N^3)$ になってダメです。
最低限必要そうな、状態として「何文字目まで作ったとき」「$1$ がいくつ続くことになるか」だけを持つことを考えます。
$\mathrm{dp}[i,j]$ を、次を満たす文字列の個数とします。
- 長さ $i$ の文字列
- 末尾が $1$
- 連続 $A$ 個以上の $0$ を $1$ に変化させたとき、連続 $B$ 個の $1$ を含まない
- 連続 $A$ 個以上の $0$ を $1$ に変化させたとき、末尾に $j$ 個の $1$ が並んでいる
長さ $i$ の文字列で、末尾が $1$ であり、連続 $A$ 個以上を $1$ にしたにときの
末尾の数が $1$ であるような状態だけを計算することにして、「001/1/1/00001/」のように、「0\cdots 01」をまとめて遷移する形で組み立てます。
遷移を $3$ 通りに分けます。おおよそ次のように遷移します。(添字が $0$ 以下や $B$ 以上のところを適当に無視すると正しいと思います)
- $0$ をはさまずに $1$ を追加した場合:$\mathrm{dp}[i,j] \leftarrow \mathrm{dp}[i-1,j-1]$
- $1$ 個以上 $A$ 個未満の $0$ を使って、$00\cdots 001$ を追加した場合:$\mathrm{dp}[i,1] \leftarrow \sum_{i-A\leq k\leq i-2,j} \mathrm{dp}[k,j]$
- $A$ 個以上の $0$ を使って、$00\cdots 001$ を追加した場合:$\mathrm{dp}[i,j] \leftarrow \sum_{k>A}\mathrm{dp}[i-k][j-k]$.
あとはこれを高速化します。$2$ 番目の遷移については、各 $k$ について $\mathrm{dp_sum}[k] = \sum \mathrm{dp}[k, :]$ も計算しながらすすめれば、全体で $\Theta(N^2)$ 時間です。(その累積和も持っておくとより良いですが、やりませんでした)。$3$ 番目の遷移については、斜め方向の累積和 $\mathrm{dp_2}[i,j] = \sum_{k\geq 0}\mathrm{dp}[i-k,j-k]$ も計算しながらすすめればよいです。(配列名は、私のコンテスト後提出:■と対応しています)。
あとで考えたところ、$\mathrm{dp}_2$ には、「右端に並んでいる $0$ を全て $1$ と見なしたときに、右端に並ぶ $1$ の個数」を状態として数え上げた配列になっているようです。
微妙にたくさんの不等式を書く必要があって、バグがこわいところです。サンプル 2 を手計算して対比しながら慎重に進めましたが、一ヶ所失敗しており、その時点でコンテスト終了 5 分前。あと一歩でACだったのですが、本番中には結果を出せませんでした。考察も実装の速度、精度がまだまだですね。

