概要
AC 人数も少なく難易度評価も高い問題ですが,解法はかなりシンプルに感じました.
考察も実装も他の方の解説より簡単にできたと感じたので,自身のロジックの確認も兼ねて解説執筆しておきます.
解法
少し変わった入力形式ですが,問題を要約すると以下の通りです:
いくつか(最大 $10^6$ 個)の組 $(a_i,b_i)$ が与えられる.数直線上の walk であって,任意の $i$ に対して $b_i$ を $a_i$ よりも後に訪れる(最初の $a_i$ への訪問よりも最後の $b_i$ への訪問の方が後である)ようなものの長さの最小値を求めよ.
$a_i<b_i$ への帰着
あらゆる $a_i, b_i$ の最小値・最大値を $L, R$ とします.$L, R$ の両方を訪れる必要があります.
最適解の構造を考えます.何らかの形で 2 回解くことにして,「$R$ を $L$ よりも先に訪れる」という仮定のもとで解きます.($a_i,b_i$ のスワップまたは座標の $-1$ 倍等をした上で 2 回解きます).
この仮定によって,$a_i\geq b_i$ を満たす組は自動的に条件を満たすので考える必要が完全になくなって,考えやすくなります.以下 $(a_i,b_i)$ と書けば $a_i<b_i$ を仮定します.
最適解の記述
まず長さ $2(R-L)$ は実現可能です.$L$ からスタートして $R$ まで往復すればよいです.以下,$2(R-L)$ 未満の長さでの目標達成の考察を前提とします.
walk の始点を $s$,walk の終点を $t$ とします.まず,$t\leq s$ を仮定できます.そうでないとすると $s, R, L, t$ をこの順に訪れるだけで長さ $2(R-L)$ 以上がかかるからです.
$[L,R]$ 内の各線分 $[x,x+1]$ に対して,次のコストを定めます:
- $[x,x+1] \subset [L,t]$ の場合:コスト $2$
- $[x,x+1] \subset [t,s]$ の場合:
- ある $i$ に対して $[x,x+1]\subset [a_i,b_i]$ ならばコスト $3$
- 任意の $i$ に対して $[x,x+1]\not\subset [a_i,b_i]$ ならばコスト $1$
- $[x,x+1]\subset [s,R]$ の場合:コスト $2$
このコストは,$s, R, L, t$ をこの順に訪れるという前提で各 $[x,x+1]$ を通る回数の下限です.
$F(s,t)$ を上で定まるコストの総和とします.ここで,次が成り立ちます:
$\mathrm{ANS} = \min\bigl\lbrace F(s,t)\mid L\leq t \leq s\leq R\bigr\rbrace$
なおここまでの議論から,$\mathrm{ANS} \geq \min\bigl\lbrace F(s,t)\mid L\leq t \leq s\leq R\bigr\rbrace$ が明らかな評価です.逆向きの不等号を以下で証明します.
証明
上の主張を示すには,次を示せばよいです:
$L\leq t\leq s\leq R$ であるとき,目的を達成する walk であって,長さが $F(s,t)$ 以下であるものが存在する(なお,この walk の始点・終点が $s,t$ にとれるとは限らない).
まず,$L, R$ の往復によりコスト $2(R-L)$ が実現できるのでしたから,コスト $1$ の区間が存在するとして示せばよいです(このことによって,以下の議論において prefix, suffix の干渉等の面倒さが生じないことが分かります).
$[t,t+1]$ や $[s-1,s]$ がコスト $1$ であるときには,次の図で示す通り,コストが $3$ であるような極大区間に対しての往復を追加しながら $s, R, L, t$ と移動します.
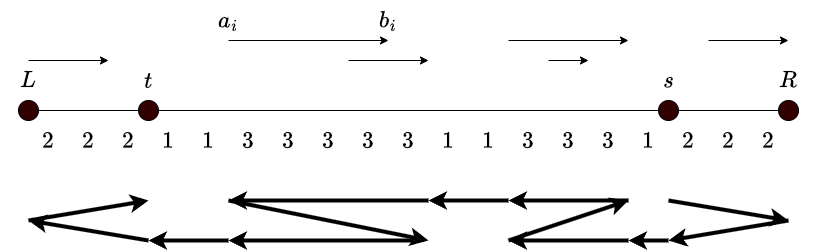
$[t,t+1]$ や $[s-1,s]$ がコスト $1$ であるという前提のもと,すべての $[a_i,b_i]$ はあるコスト $2$ 以上の区間に含まれているので,これで目的を達成しています.
suffix のコスト $2, 3$ の区間がつながっている場合にも,($s$ でない始点を使い)これらの区間をまとめてとればよいです.なおこの場合には $F(t,s)$ 未満の長さを達成できます.
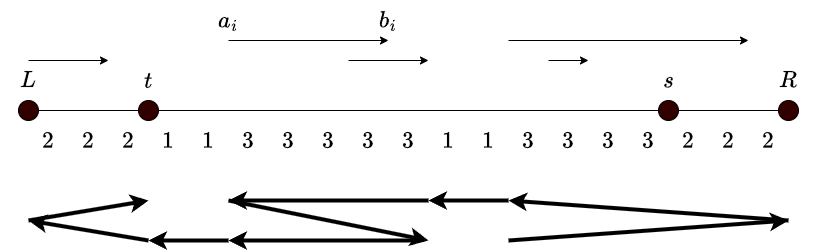
以上により証明できました.
答の計算
ここまでくればかなり簡単な問題です.$[x,x+1]\subset [t,s]$ に対するコストが $s,t$ に依存しないことに注意してこれらのコストの和を累積和の差分で表すと,おおよそ次のような形に式変形可能です:$\mathrm{ANS} = \min\bigl\lbrace f(s)+g(t)\mid L\leq t \leq s\leq R\bigr\rbrace$.
あとは各 $[x,x+1]$ を含む $[a_i,b_i]$ が存在するか等の前計算を行った上で $t$ ごとにこの計算をすることを考えると,簡単に計算できると思います.
空間 $O(N)$,時間 $O(N+M)$ で計算できます.

