概要
設定されている難易度(★の数)に比べてかなり簡単に感じた.
解法
今まで訪問したことがあるタイルの集合を単に状態と呼ぶことにします.答は次のように書けます.
白マスが存在するようなすべての状態 $S$ に対する,$a(S)b(S)$ の総和.$a,b$ は以下で定義する.
- $S$ に到達する確率 $a(S)$
- はじめて $S$ に到達した時点から,別の状態に到達するまでの動作回数期待値
円環を忘れて,$S$ を数直線上の区間 $[-L,R]$ と見なしたとき,次が成り立ちます.
- $a(S) = 1/(L+R+1)$.
- $b(S) = L+R+1$.
証明は後述します.したがって,本問の答は白マスが存在するような状態 $S$ の数え上げと一致します.あとは $L$ ごと(または $R$ ごと)に計算することを考えれば,累積和と尺取り法で $O(N)$ 時間で答が求まります.
証明
少し計算すれば証明できます.だいたい次のことを考えればよいです:
いま状態が $[0,n]$ であり,$x=0$ に居る.左右に等確率で移動することを繰り返す.$-1, n+1$ のどちらかに初めて到達するまでの移動回数の期待値や,その時点でのそれぞれの地点への到達確率を求めよ.
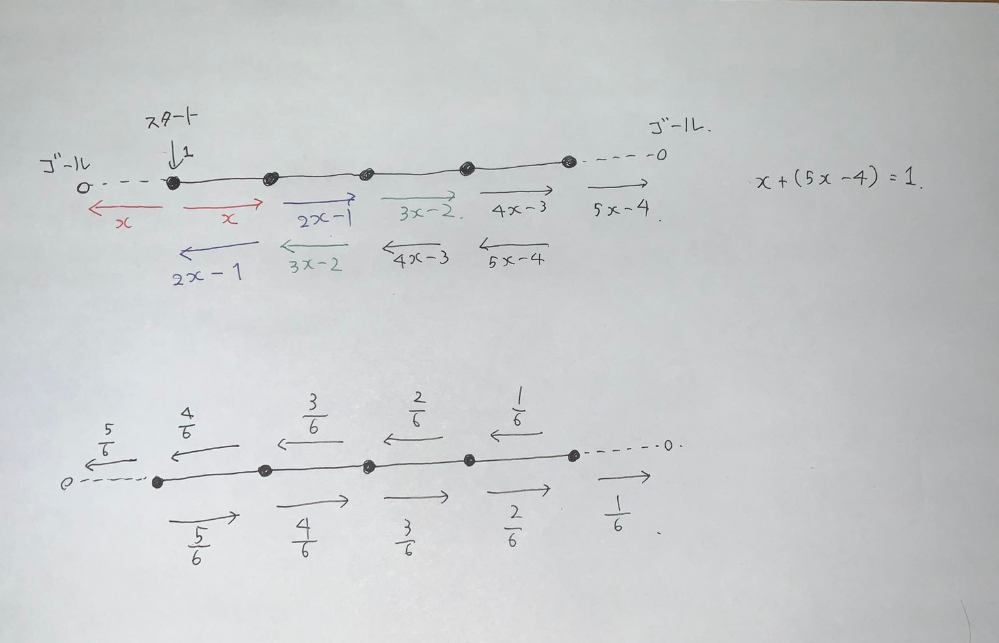
各有向辺の移動回数期待値を考えると計算しやすいです.各地点から左右方向への移動回数期待値は等しいです.また,$x=0$ においてはその点に入る回数よりも出る回数が $1$ 多いこと,$x\in [1,n]$ についてはその点に入る回数と出る回数が等しいことなどから図の上のような関係が成り立ちます.さらに $x=-1,n+1$ への到達回数の和が $1$ であることからすべての有向辺の回数期待値が決まります.
結局,$[0,n]$ から $x=-1$ に到達する確率が $n/(1+n)$,$x=n+1$ に到達する確率が $1/(1+n)$ であることなどが分かります.ここから順に $a(S)$ を定めていくことができます.
$b(S)$ はすべての有向辺の使用回数の総和で,これも簡単に計算できます.

