概要
多項式の変数変換を使わずに解きます.
解法
$A_i$ の寄与係数を求めればよいです.左右独立に解けばよいです(これらは公式解説と同じ).
簡単のため $S$ の先頭に $s$ を付け加えておきます.$S$ を reverse しておきます.次の問題を解けばよいです.
列 $X = [0, 1, \ldots, n-1]$ に対して,$S$ の先頭の文字から順に
- 文字が a ならば $X$ の prefix を消去する
- 文字が s ならば $X$ の subsequence を消去する
ことを順に行って最終的に空文字列にする方法を数えよ.
例えば $S$ が $sssasas$ であるとし,これを $s_0s_1s_2a_0s_3a_1s_4$ と書くことにします.$X$ の各要素がどの文字によって消されるかを書いた列を考えます.これを $a_i$ で区切ってみます.次のような見た目になります.
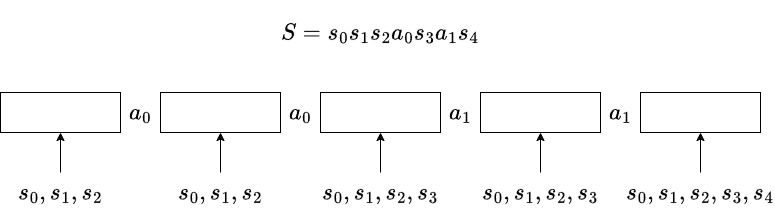
各 $a_i$ は $0$ 回含め何回現れてもよいですが,その添字は昇順です.
各 $a_i$ の左には $S$ で $a_i$ よりも左にあった文字だけが来れるので,$a_i$ で区切った各部分ごとにどの $s_j$ が並べられるかが決まります.逆にこの形の並び順に対して対応する消去手順が一意に存在します.
すると,まず各 $a_i$ の現れる回数を固定したときに求めたいものがどうなるかが計算できます.
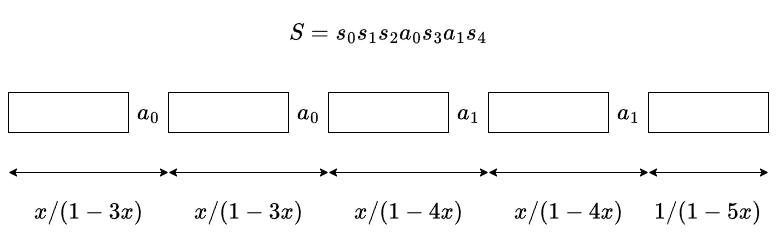
$a_i$ の現れる回数 $n_i$ を固定すると,計算したいものは $f_0(x)^{n_0}f_1(x)^{n_1}\cdots \cdot \frac{1}{1-mx}$ という形で書けることが分かります.
$n_i$ を自由にとれるとして計算するには,各 $i$ に対して $F_i(x)=\sum_{n=0}^{\infty}f_i(x)^n=\frac{1}{1-f_i(x)}$ に置き換えた $F_0(x)F_1(x)\cdots \cdot \frac{1}{1-mx}$ を求めればよいです.
各 $f_i$ は $x/(1-cx)$ の形で $F_i$ も 1 次式の商として表せます.よって求めたい形式的べき級数は $1$ 次式の積を $1$ 次式の積で割ったものという形でかける有理式です.
結局 $O(M)$ 個の $1$ 次式の総積を $N$ 次程度まで計算する問題が解ければよく,これは $O(M\log^2M + N\log N)$ 時間で行えます.

