概要
解説では、かなりあっさりと、二分探索を主張していますが、正当性の確認はそんなに簡単ではないと思います。参加者も、(難易度表記やAC人数から類推してというのならともかく)自明に二分探索だと思った人は、もう少し正当性の確認に注意した方が良いのではないでしょうか?
難易度も★2への投票が多いですが、そんなに簡単ですか?うーん。
私は結構難しい問題だと思いました。解けたので、書きます。
二分探索できるのは?
実数 $L\leqq x\leq R$ に関する命題 $P(x)$ があるとき、$P(x)$ が成り立つような $x$ の上限を求めたいとします。これが単純な二分探索で求められるのは、条件に単調性がある場合です。

区間の上限の設定
今回は、$f(x) = x^2 – Qx\log_2 x – P$ としたとき、$f(x) \leqq 0$ となる $x \in [1, \infty)$ の上限を求める問題です。 このままでは長さ無限大の区間で困りますが、$x > R\implies f(x) > 0$ となるような $R$ をとって $[1,R]$ 上で二分探索すればよいです。
例えば、$R = 10^{11}$ は妥当な選択肢です。証明も難しくはないです。例えば次が一例です。
- $x > 4\implies \log_2 x < \frac{x}{2}$ を示す。例えば $\frac{x}{2} – \log_2 x$ は下に凸な関数で、$x=2,4$ を零点に持つことから示せます。
- $x > 4^{10}\implies \log_2 x^{0.1} < \frac{x^{0.1}}{2}$ が分かる。$x > 4^{10} \implies \log_2 x < 5x^{0.1}$ が分かる。
- $x > 4^{10}\implies f(x) = x^2 – Qx\log x – P > x^2 – 5Qx^{1.1} – P = (x^{0.9} – 5Q)x^{1.1} – P$.
- よって、問題の制約のもと、$x > 10^{11}$ に対して $f(x) > (10^{9.9} – 5\cdot 10^9)10^{12.1} – 10^9 > 0$ となって示された。
$f$ の増減に対する考察
一般には、$f$ は単調増加ではないので、二分探索が使えるかどうかの考察は少し大変です。まあ、高校数学典型を使って $f$ の増減を調べましょう。python を使っている場合は、sympy を利用すると簡単です。
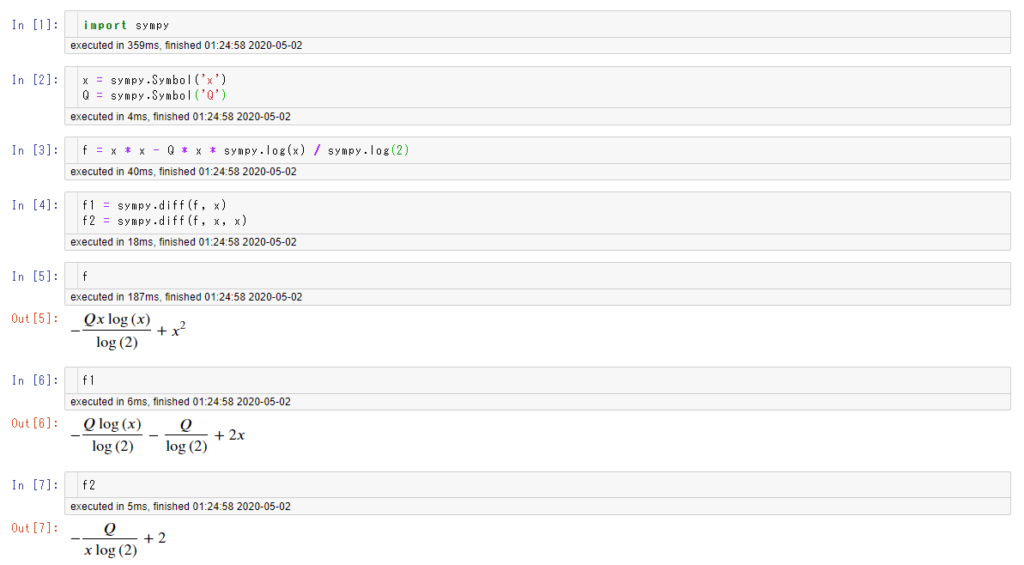
$f$ の増減を調べることは、$f'(x)$ (上で $f1$ となっているもの)の正負を調べることに対応します。
次のように場合分けをします。
$Q \geqq 2$ の場合
$x_0 = \frac{Q}{2\log 2}$ とします。 $Q \geqq 2$ のとき、$x_0 > 1$ が確かめられます。また、$f'(1) = 2 – \frac{Q}{\log 2}$ ですが、$Q \geqq 2$ のもとで範囲で $f'(1) < 0$ です。したがって、$f'(x)$ の増減表は次のようになります。
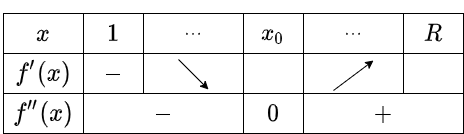
また、$f(1) < f(R)$ より、$f'(x) > 0$ となる $x \in (1,R)$ が存在します。よってある $x_1\in [x_0,R]$ が存在して、次が成り立ちます:$$x\in [1, x_1]\implies f'(x) \leqq 0, \qquad x\in [x_1,R]\implies f'(x) \geqq 0$$
つまり、$f$ は、ある点 $x_1$ を境に、単調減少から単調増加へと切り替わります。このことと $f(1) \leqq 0$ を合わせて、判定問題 $f(x) \leqq 0$ は $x$ について単調性を持つことが示せました。
$Q = 1$ の場合
$x_0 = \frac{Q}{2\log 2}$ とします。$x > x_0 \implies f”(x) > 0$ でした。ところで、 $Q=1$ のとき、$x_0 < 1$ となります。したがって、$[1,R]$ において常に $f”(x) > 0$ で、$f'(x)$ は単調増加になります。
$f'(1) = 2 – \frac{Q}{\log 2} > 0$ なので、$[1,R]$ において $f(x)$ は単調増加です。よって、この場合はさらに容易に判定問題の単調性が従います。
とても細かいこと
ところで、$f(x) \leqq 0$ となる $x$ の最大値(上限ではなく)を求める問題です。
集合 $\{x\mid x < 1\}$ に最大値が存在しないように、それっぽい境界(上限)があっても「最大値」があるとは限りません。
今回の問題では、条件が $f(x) \leqq 0$ ではなく $f(x) < 0$ だったりすると最大値がないので、結構きわどいですね。本問題での最大値は、上で行った考察によれば単調連続関数の零点ですから、中間値の定理により存在します。(大学 1 年生程度?の解析学を知っていれば、増減の詳しい考察をせずともコンパクト集合の性質としてすぐに導けます。)
追記
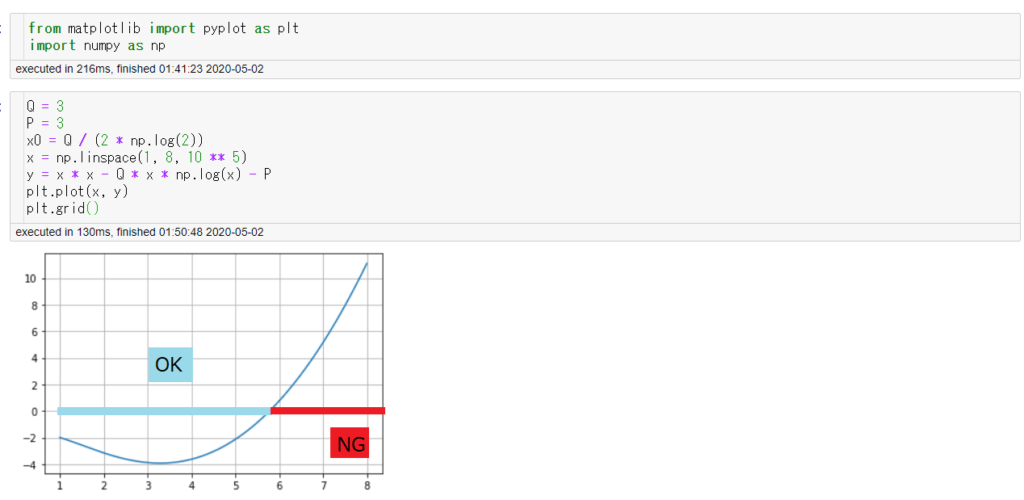
$x\geqq 1$ に限定しなければ、判定問題 $f(x)\leqq 0$ が単調性を満たさない場合があります。例えば、$P,Q$ に小数も許すと $[0, \infty)$ での二分探索は、誤答になります。

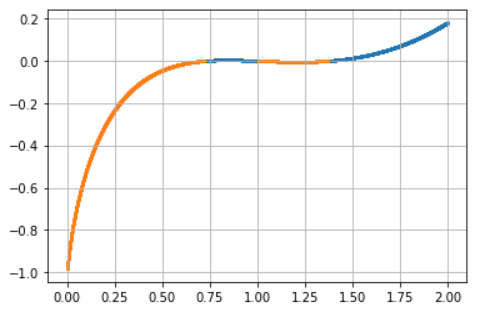
判定問題が単調性を満たさず、最大の解を見落としてより小さな境界を検出していますね。

