お絵描きをしました。
重心分解
木の重心の定義や計算方法については省略します.
重心分解の図示
木の重心のひとつを求め,重心を取り除き連結成分に分けることを繰り返します.
各ステップにおいて,重心のひとつを根にとり,根が最も上側に来るような図示をしています.
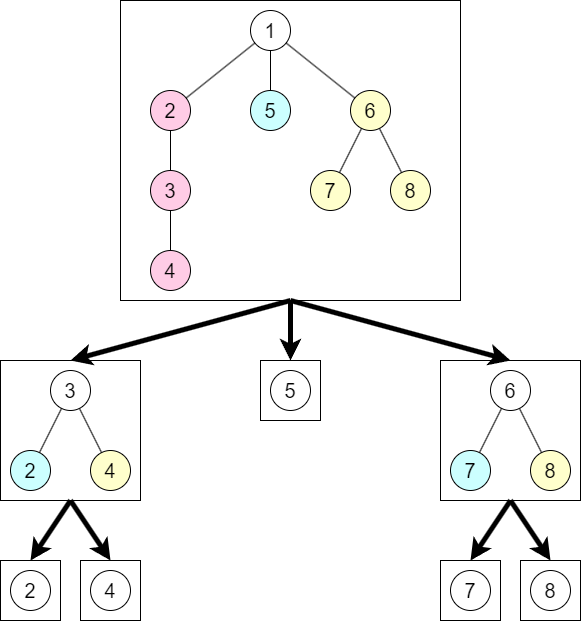
各ノードが根付き木を表すような木構造が得られます.
元の木の頂点数を $N$ とします.
子ノードに進むたびに木の頂点数が半分以下になるため,この木の深さは $O(\log N)$ です.したがって頂点 $v$ を固定したとき,$v$ を含むノードの個数は $O(\log N)$ です.各ノードの表す根付き木の頂点数の総和は $O(N\log N)$ となります.
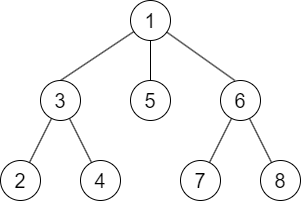
なお,上図において各ノードの根同士を結んで得られる木のことを指して重心分解と呼ぶ流儀もあるようです.筆者の経験上,競技プログラミングにおいては,各ノードとして現れる部分木のリストのみが重要であることが多く,重心を結んで得られる木の構造(例えば各頂点の親がどの頂点であるかといった情報)そのものは不要なことが多いです.ただし,この木の構築を題材とした出題も稀にあります(https://atcoder.jp/contests/abc291/tasks/abc291_h).
パスに対する計算の分割
以下では単にパスと言えば,辺の個数が 1 個以上あるものを指すこととします.
重心分解の競技プログラミングにおける主要な用途は,「木上のすべてのパスに対する何かを計算せよ」という種類のものです.例えば
- https://judge.yosupo.jp/problem/frequency_table_of_tree_distance
- https://atcoder.jp/contests/yahoo-procon2018-final-open/tasks/yahoo_procon2018_final_c
などが代表例です.
あるノードの表す木おいて,パスを「根(重心)を通るか否か」で場合分けして考えましょう.「根を通らないパス」は,「子ノードの表す木のパス」であると言い換えられます.したがって各ノードにおいては,根を通るパスの計算に専念すればよくなります.$n$ 頂点のノードでこの計算が $O(n)$ 時間で行えるなら全体で $O(N\log N)$ 時間,$O(n\log n)$ 時間で行えるなら全体で $O(N\log^2N)$ 時間などとなります.
結局重心分解を行うと,$n$ 頂点の根付き木に対して,「根を通るパス」全体に対する計算を $O(n)$ 時間などで行う問題に帰着できることになります.
根を通るパスに対する計算
木上のパスを扱う問題において,考察対象が根 $r$ を通るものに限定される利点は,任意のパス $uv$ が $ur, rv$ の結合として表されることにあります.そのためすべての $u, v$ でパス $ur$, $rv$ に対する何かを前計算しておくことで,おおよそ次のような問題に帰着できます.
各頂点に対してパス $ur, rv$ の値 $a_u, b_v$ という値が定まっている.パスの結合を表す関数 $f$ がある.すべての $f(a_u, b_v)$ に対して何かの処理をせよ(総和などの計算,条件を満たすものの数え上げなど).
一方でこの場合には,$(u, v)$ として任意の頂点対を考えてはいけないことに注意する必要があります.根 $r$ に対して同じ側の部分木に含まれる $(u,v)$ に対して,パス $uv$ は根 $r$ を通らないためです.
各部分木の頂点に何らかの色をつける(最初の重心分解の図を参照)ことにすると,
2 頂点の組 $u,v$ であって色が異なるものすべてに対する $f(a_u,b_v)$ に対して何かの処理をせよ.
といったタイプの問題に対応する必要が出てきます.
- 総和のような計算であれば,「任意の 2 頂点の組に対する総和」から「同色の 2 頂点の組に対する総和」を引く.
- max のような計算であれば,「$a_u$ や $b_v$ の max を,2 色分保持する」.
といった対処法がとれる場合があります.
一方で逆元のない区間作用などの問題を考えると,この「色が異なる」という部分が弊害となってしまう場合があります(https://suisen-kyopro.hatenablog.com/entry/2022/03/21/220009).
色をさらに二分していく分割統治を考えると解決することもありますが,最悪計算量の悪化に対応するのは少し大変です.https://noshi91.hatenablog.com/entry/2022/03/27/042143 では Huffman coding を利用してこの問題に対処しています.
1/3 重心分解
1/3 重心分解の図示
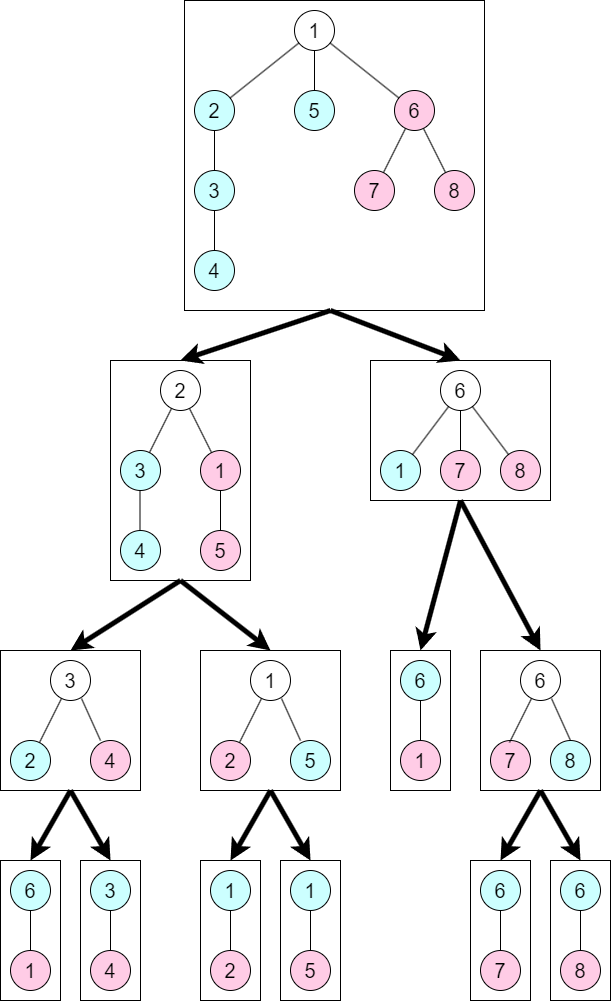
各ノードで「赤点と青点を結ぶパス」を考えることで,すべてのパスがちょうど 1 回ずつ現れるようにすることが目標です.次のような手順になります.
- あるノードの持つ部分木が 2 頂点であるならば,2 点をそれぞれ赤・青として終了.
- そうでないならば,重心を根として根付き木にする.根の周りの部分木を,辺がだいたい半分ずつに分かれるように 2 色で塗り分ける.各色の頂点と根を合わせて子ノードとする.
各ノード,子ノードの木に含まれないパスがどのようなものかを考えると,赤点と青点を結ぶパス全体であることが確かめられます.したがって各ノードにおいて赤点と青点を結ぶパスを考えると,全てのパスをちょうど 1 回ずつ考えることができます.
「辺がだいたい半分ずつに分かれるように」という部分については単純な貪欲法によって $[1/3,2/3]$ の割合が実現できることが https://codeforces.com/blog/entry/104997 で解説されています.
これによって「すべてのパスに対する計算」を「赤色の頂点 $u$, 青色の頂点 $v$ に対する $f(a_u,b_v)$ の計算」に変換可能になります.
計算量について考えましょう.木構造を辺集合の分割として捉えます.各ステップで辺の個数が $2/3$ 以下になることから深さが $O(\log N)$ であることが分かります.したがって各辺に対してそれを含むノードは $O(\log N)$ 個です.このことからノードごとの木の大きさの総和は $O(N\log N)$ であることが分かります.
始点を固定したパスに対する処理
一方で 1/3 重心分解では,木の分割の際に頂点が分裂してしまうため,ひとつの頂点 $v$ に注目したときに $v$ が現れるノードの個数が抑えられないという欠点があります(例えばスターグラフを考えると,ひとつの頂点がすべてのノードに現れます).
このことは,「始点を固定したパス全体」を扱う際に障害となります.
- https://atcoder.jp/contests/yahoo-procon2018-final-open/tasks/yahoo_procon2018_final_c
- https://judge.yosupo.jp/problem/vertex_add_range_contour_sum_on_tree
1/3 重心分解の枠組みでこの障害を克服する方法について説明します.次のツイートも確認しながら図を見てください.
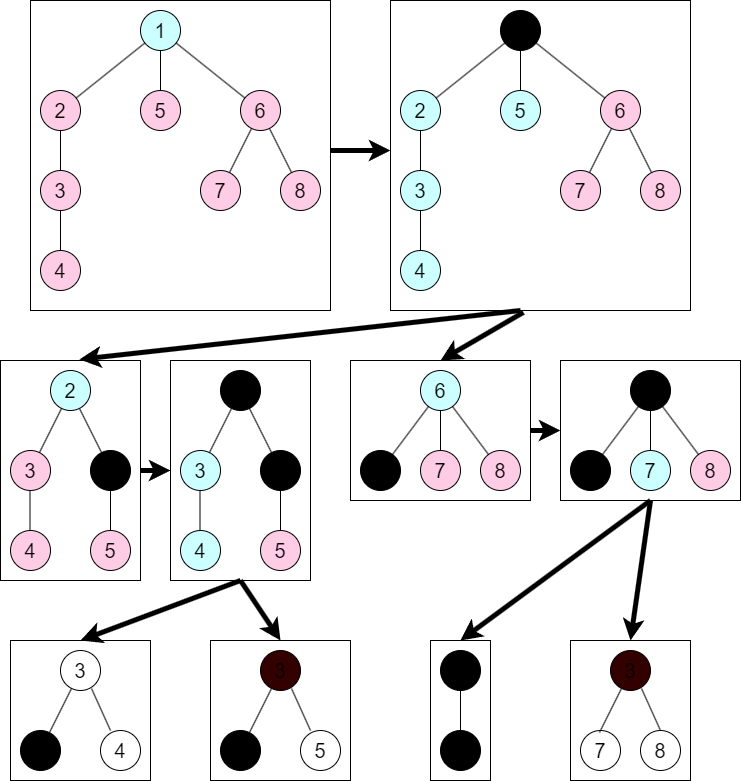
黒塗りの頂点は virtual な頂点を表します.また,全部を図示すると図が巨大になるため途中で打ち切っています.
次のような操作を繰り返しています.
- 重心を根に選ぶ.
- 根が real ならば,根を青点,その他の real な頂点を赤点として図示している.根を virtual に変更したものを子ノードとする.
- 根が virtual ならば,辺の個数がだいたい半分になるように 2 色で塗る.この分割にそって木を 2 分割する.
各ノードにおける real vertex 同士を結ぶパスが,そのノードにおける赤・青の頂点を結ぶパス,または子ノードにおける real vertex を結ぶパスとなっていることを確認してみてください.「まず根を端点とするパスを処理してしまう」という点を除けば通常の 1/3 重心分解と同じことです.
上で最も葉に近い部分は図示していませんが,適切に処理してください.
各頂点が real であるようなノードが $O(\log N)$ 個であるため,始点ごとのパスを扱う問題でも重心分解と同様の計算量が達成できるようになります.
一方で頂点が virtual vertex として現れる回数は抑えることができないため,頂点属性に変更クエリが来て,パスの情報がパスが通る頂点の変更の影響を受けるような場合にはこの手法は適用できないかもしれません.

