FPS 合成・逆関数の解説（１）逆関数と Power Projection

2024.04.21

For English Readers → FPS Composition and Compositional Inverse (Part 1)

スポンサーリンク

概要

noshi91 さんにより，形式的べき級数の合成・逆関数を $\Theta(n\log^2 n)$ 時間で計算する方法が発表されました．https://noshi91.hatenablog.com/entry/2024/03/16/224034

これは基礎的な問題に対して簡潔なアルゴリズムで既知の計算量を改善するもので，国内・国外問わず多くの関心を集めました．

その後，合成アルゴリズムの転置原理を用いたより簡潔な導出（Elegia さん，hos_lyric さん）や，それらの定数倍の良い実装について考察（Nachia さん等）がされています．このことについて学べる記事があまりないように感じたので，私の方でもある程度解説してみることにします．（発見者等については私の認識を書いていますが，不適切な部分があれば指摘してください．）

記事 (1), (2) の 2 つに分けて解説することを予定しています．本記事 (1) では逆関数および，その計算に用いられる Power Projection のアルゴリズム・実装を扱います．記事 (2) で，転置原理を利用した合成アルゴリズムの導出や実装を扱う予定です．

次回 → FPS 合成・逆関数の解説（2）転置原理による合成アルゴリズムの導出

本記事では多項式・FPS の畳み込みが $\Theta(n\log n)$ 時間で行えることを仮定します．競技プログラミングでの利用に興味がある場合，適当な素数 $p$ をとって係数を $\mod p$ で考えていると思っていただいて構いません．また，FFT, NTTを区別せず FFT と表記します．

参考文献

逆関数と Power Projection

$f$ を $[x^0]f=0, [x^1]f\neq 0$ であるような FPS とするとき，これの逆関数（compositional inverse）つまり $g(f(x))=f(g(x))=x$ となる $g$ が唯一存在することが証明できます．

$c=[x^1]f$ とします．$f(x)/c$ の逆関数が $g(x)$ であるとき $g(x/c)$ が $f(x)$ の逆関数となることが容易に分かります．したがって逆関数を求める問題は，$[x^1]f=1$ の場合に帰着できます．

このとき $f$ の逆関数 $g$ は $[x^0]g=0, [x^1]g=1$ を満たします．

$f$ の $n$ 次以下の部分が与えられていて，$g$ の $n$ 次以下の部分を求めることを考えます．ラグランジュ反転公式より任意の $i$ に対して

$$n[x^n]f(x)^i = [x^{n-i}]i\cdot (g(x)/x)^{-n}$$

が成り立ちます．$i=1,\ldots,n$ に対して左辺を求めることができれば，$(g(x)/x)^{-n}$ が $n-1$ 次まで求まることになり，その $-1/n$ 乗をとることで $g(x)/x$ が $n-1$ 次まで求まります（$-1/n$ 乗が定義できることおよびそれが $g(x)/x)$ と一致することに $[x^1]g=1$ が必要です）．したがって $g(x)$ が $n$ 次まで求まります．

結局，逆関数を求める問題は次の計算に帰着できます：

$i=1,\ldots,m$ に対して $[x^n]f(x)^i$ を求めよ．

これは，以下に解説する Power Projection と呼ばれる問題の特殊ケースです．noshi91 さんの手法は，Power Projection を $\Theta(n\log^2 n + m\log m)$ 時間で解くものです．したがって，逆関数を求める問題は $\Theta(n\log^2 n)$ 時間で解けることになります．

以下，Power Projection を解くアルゴリズムや，その高速な実装方法を解説します．

Power Projection のアルゴリズム

FPS のべき乗（power）の係数の適当な重みでの線形結合（projection）を列挙するという次の問題を考えます：

[Power Projection] 数列 $w_0, \ldots, w_{n-1}$ および FPS $f(x)$ が与えられる．$i=0, \ldots, m-1$ に対して次を求めよ：$\sum_{j=0}^{n-1}w_j\cdot [x^j]f(x)^i$．

なお本記事では，説明を簡潔にするために，以下 $n$ が $2$ のべき乗であることを仮定します． 必要があれば $f, w$ の末尾に $0$ を追加することでこの場合に帰着できます．（説明の簡略化だけでなく，計算量の定数倍が変わらないまま実装の場合分けを少し減らすことが出来て便利だと考えています）．

$w_j$ の代わりに $g(x)=\sum_{j=0}^{n-1}w_{n-1-j}x^j$ を考えると，問題は次のように言い換えられます．

FPS $f(x), g(x)$ が与えられる．$i=0, \ldots, m-1$ に対して $[x^{n-1}]g(x)f(x)^i$ を求めよ．

$2$ 変数 FPS を考えれば $g(x)f(x)^i = [y^i]\dfrac{g(x)}{1-yf(x)}$ です．したがって $P(x,y)=g(x)$, $Q(x,y)=1-yf(x)$ とおけば，計算したいものは $[x^{n-1}]P(x,y)Q(x,y)^{-1}$ ということになります．

これを Bostan-Mori のアルゴリズム と同様の $Q(x)Q(-x)$ テクニック（Graeffe’s method）により計算します．

$n$ が $2$ 以上の $2$ べきであるとします．次の式変形を利用します：$$[x^{n-1}] P(x,y)Q(x,y)^{-1} = [x^{n-1}]P(x,y)Q(-x,y)\cdot (Q(x,y)Q(-x,y))^{-1}$$

$Q(x,y)Q(-x,y)$ は $x$ の偶関数であり，ある $Q_1(x,y)$ に対して $Q(x,y)Q(-x,y)=Q_1(x^2,y)$ が成り立ちます．$P(x,y)Q(-x,y)$ の部分を $x$ について奇数次・偶数次の部分に分けて $P(x,y)Q(-x,y) = xP_1(x^2,y)+P_2(x^2,y)$ と書くことにすると，

$$[x^{n-1}] P(x,y)Q(x,y)^{-1} = [x^{n-1}]xP_1(x^2,y)Q_1(x^2,y)^{-1} + [x^{n-1}]P_2(x^2,y)Q_1(x^2,y)^{-1}$$

となりますが，$n\geq 2$ が $2$ のべき乗であることを思い出すと，$[x^{n-1}]P_2(x^2,y)Q_1(x^2,y)^{-1}$ は明らかに $0$ です．したがって

$$[x^{n-1}] P(x,y)Q(x,y)^{-1} = [x^{n-1}]xP_1(x^2,y)Q_1(x^2,y)^{-1} = [x^{n/2-1}]P_1(x,y)Q_1(x,y)^{-1}$$

が得られます．求めるべきものを考えると $P_1, Q_1$ については $n/2-1$ 次までしか保持する必要がないことにも注意してください．

これは問題の形を保ったまま $n$ の大きさを $1/2$ 倍にしたという式変形になっており，これを $\log_2n-1$ 回繰り返すことで $n=1$ の場合に帰着することができます．$n=1$ になったら最終的には 「$p(y)/q(y)$ を $m-1$ 次まで求めよ」というタイプの問題になり，これはただの FPS 除算です．まとめるとおおよそ次のアルゴリズムにより答を求めることができます：

  • $P_0(x,y)=g(x), Q_0(x,y)=1-yf(x), n_0=n$ とする．
  • $n_k=1$ となるまで次によって $P_k, Q_k$ を定める：
    • $P_k(x,y)Q_k(-x,y)$ の $x$ について奇数次の部分を $n_k/2$ 項分取り出して $P_{k+1}(x,y)$ とする．
    • $Q_k(x,y)Q_k(-x,y)$ の $x$ について偶数次の部分を $n_k/2$ 項分取り出して $Q_{k+1}(x,y)$ とする．
    • $n_{k+1}=n_k/2$ とする．
  • $n_k=1$ であるとき，$P_k(x,y)Q_k(x,y)^{-1}$ は $1$ 変数 FPS の除算になっている．これの $m-1$ 次までを求めて出力する．

なお，$[x^0]f=0$ の場合には常に $[x^0]Q_k=1$ が成り立ち，出力すべきものは単に $P_k(x,y)$ となります．一般の power projection は $\sum_j w_j[x^j](f(x)+c)^i=i!\cdot \sum_{p+q=i}\dfrac{w_j}{p!}[x^j]f(x)^p\cdot \dfrac{c^q}{q!}$ などの式変形により $[x^0]f=0$ の場合に帰着できるので，$[x^0]f=0$ の場合に特殊化した実装をしてしまうのも良いでしょう（本記事内で紹介する私の実装例はそのようにしています）．

計算量を解析するために，各 $P_k, Q_k$ の次数について考えます．例えば $n=16$ のときは次のようになります．$i$ 行 $j$ 列に $x^iy^j$ の項があると思ってみてください．

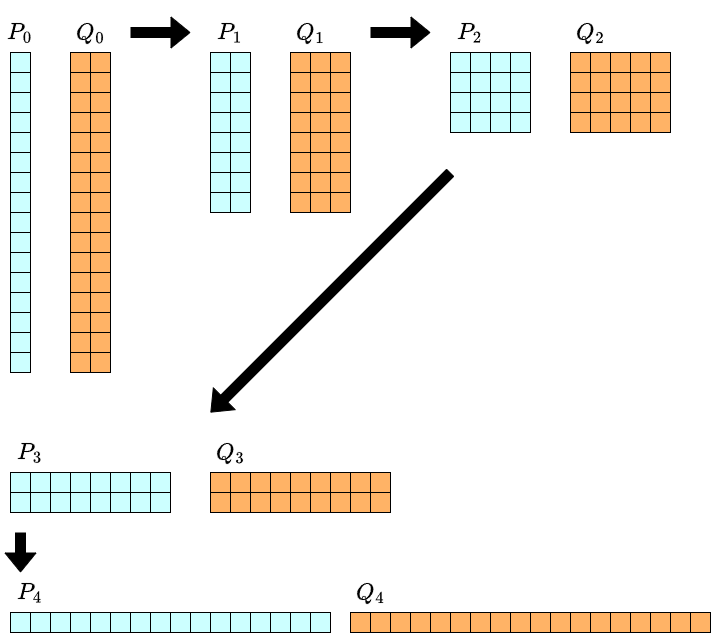
$y$ の次数については計算を進めるについて $2$ 倍ずつ長くなります．一方で，$x$ の次数については半分ずつになるのでした．したがって反復の各段階で，保持すべき項の個数は常に $\Theta(n)$ 個です．そのような形の $2$ 変数多項式の積（$2$ 次元畳み込み）は，$\Theta(n\log n)$ 時間で行えます．この反復を $\log_2 n$ 回行ったあと最後に $m-1$ 次までの形式的べき級数除算を行うため，全体の計算量は $\Theta(n\log^2 n + m\log m)$ となります．

上のアルゴリズムの各反復について，より詳しく見ましょう．

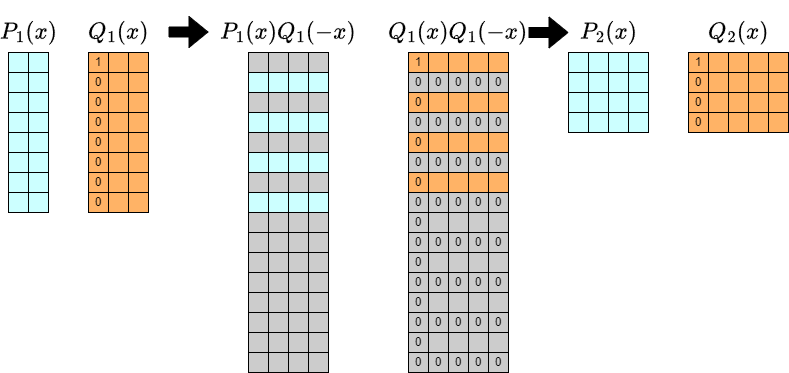
計算したいものの $y$ 方向の長さが $2^k+1$ になっているのが，いかにも畳み込みと相性が悪くてそのまま計算すると定数倍を悪化させそうです．

一方で，$Q(x,y)=1-yf(x)$ であったことから必ず $[y^0]Q_k=1$ であることが分かります．したがって $Q_k$ の次数がうっとおしい問題は，$[y^0]$ 部分を適切に特殊処理することにより解決できそうです．

それはそれで統一的な扱いをする部分の次数が $[1, 2^k]$ となるのが実装における面倒要素となりそうですが，この点については 「$y$ 方向に reverse したものを考える」ことで簡潔な実装が可能となります．これは高速化のために必要というわけではありませんが，私もかなり考えやすくなると感じたため本記事でも採用します．

アルゴリズムそのものを少し修正して次のようにします．

  • $P_0(x,y)=g(x), Q_0(x,y)=-f(x)+y, n_0=n$ とする．
  • $n_k=1$ となるまで次によって $P_k, Q_k$ を定める：
    • $P_k(x,y)Q_k(-x,y)$ の $x$ について奇数次の部分を $n_k/2$ 項分取り出して $P_{k+1}(x,y)$ とする．
    • $Q_k(x,y)Q_k(-x,y)$ の $x$ について偶数次の部分を $n_k/2$ 項分取り出して $Q_{k+1}(x,y)$ とする．
    • $n_{k+1}=n_k/2$ とする．
  • $n_k=1$ であるとき，$P_k(x,y)$, $Q_k(x,y)$ を reverse したもの $p(y), q(y)$ とし（より形式的には $p(y)=y^{n-1}P_k(x,1/y)$ など），$p(y)q(y)^{-1}$ の $m-1$ 次までを出力する．

すると，各時点で $Q_k$ の $y$ についての最高次数の項は唯一の項 $y^{2^k}$ になり，次数 $[0,2^k-1]$ 部分を適切に畳み込みつつ $2^k$ 次部分を適切に特殊処理するという実装方針になります．

高速化に強い関心がない場合は，ここまでの理解に基づいて実装すればよいでしょう．$2$ 次元畳み込みが必要となりますが，例えば次の実装例のように $2$ 変数多項式の $(i,j)$ 成分を 1 変数多項式の $Wi+j$ 成分に対応させるという要領で $1$ 次元畳み込みに帰着すれば，豊富なライブラリ準備がない場合でも簡単に実装できると思います．

実装例（1083ms）：https://judge.yosupo.jp/submission/203740

上の実装例ではアルゴリズムの動作を分かりやすくするため，$2$ 次元配列を $1$ 次元配列になおし，畳み込んだあと再び $2$ 次元配列に戻しています．はじめからすべてを $1$ 次元配列で実装してしまうこともできて，例えば次のような実装が可能です．実行時間の改善は少ないですが，かなりのメモリ節約（および実装の簡略化）が出来ていると思います．

実装例（1042ms）：https://judge.yosupo.jp/submission/203746

Power Projection の FFT を利用した高速化 (案1)

多項式の FFT が可能であるとき，より定数倍の良い実装が可能になります．高速化手法の多くは

と共通なので，以下の議論に慣れがない場合には先にこちらの問題の高速化に取り組んでも良いかもしれません．次の資料も役に立つと思います．

$x$ について $a-1$ 次，$y$ について $b-1$ 次の多項式を型が $(a,b)$ の多項式ということにします．

各反復の開始時点で，$P=P_k, Q=Q_k$ の型が $(n,m)$ であるとします．$R(x)=Q(-x)$ と書くことにします．$P(x)R(x)$ や $Q(x)R(x)$ の適当な部分を取りだしたものが求めたいものです．

$P(x)R(x)$ や $Q(x)R(x)$ は次の手順で計算できます．

  • $P(x),Q(x),R(x)$ を $0$ 埋めして型 $(2n,2m)$ に拡張する．$[x^0]Q(x)$ に $y^m$ を加える．
  • $P,Q,R$ を長さ $(2n,2m)$ でフーリエ変換したもの $\mathcal{F}[P], \mathcal{F}[Q], \mathcal{F}[R]$ を計算する．これは各軸方向に FFT すれば計算できる．
  • $\mathcal{F}[P]$ と $\mathcal{F}[R]$ の各点積をとったものは $PR$ のフーリエ変換 $\mathcal{F}[PR]$ である．これを逆フーリエ変換することで $PR$ が求まる．
  • $QR$ も同様である．逆フーリエ変換の出力は $Q(x)R(x)$ の長さ $(2n,2m)$ での巡回畳み込みである．よって $y^{2m}$ となるべき項が $1$ になっているのでその分を修正する必要がある．

したがって必要な計算はフーリエ変換 $3$ 回，逆変換 $2$ 回ということになりそうですが，さらに次の性質を用いるとフーリエ変換の回数を $2$ 回にできます：

  • $\mathcal{F}[R]$ は $\mathcal{F}[Q]$ から読み取れる．特にフーリエ変換を bit reverse 順に並べる実装では，$\mathcal{F}[Q]$ の $2i+0$ 番目・$2i+1$ 番目が $\mathcal{F}[R]$ の $2i+1$ 番目・$2i+0$ 番目に一致するという簡潔な対応がある（参考記事内「$f(-x)$ の DFT の計算」）．特に実装内で $R$ を定義したりそのフーリエ変換をする必要はない．

実装例（725ms）：https://judge.yosupo.jp/submission/203748

さらに参考記事内「偶数部分 (奇数部分) だけ IDFT」のテクニックにより，$P(x)R(x)$ の奇数部分，$Q(x)R(x)$ の偶数部分のフーリエ変換を直接計算できます．奇数部分の取り出しのためには $\omega_{2n}^{n+j}$ 部分の計算が必要になるので前計算しておきましょう．あとは逆変換をして上半分を取り出せばよいです．

実装例（586ms）：https://judge.yosupo.jp/submission/203750

さらに各反復の最初と最後に注目すると，「長さ $2m$ の列を逆フーリエ変換し，それを長さ $4m$ でフーリエ変換する」という処理が行われていることが分かります．これは参考記事内「2 倍の長さの DFT の計算」の方法で高速化可能です．常に $P, Q$ を $y$ 方向にフーリエ変換したもののみを保持するようにして，$y$ 方向のフーリエ変換の代わりにこの doubling を行い，最後のフーリエ逆変換を行わないようにします．$Q(x,y)$ の $y^m$ の部分の補正もこれを踏まえて修正する必要があることに注意しましょう．

これも FFT の総量を減らす定数倍高速化になっているはずですが，私が思ったよりも実行速度の改善は少なかったです．

実装例（574ms）https://judge.yosupo.jp/submission/203752

なお，計算は $y$ 方向への doubling を除いて $j$ ごとに独立な計算となっています．すべての $j$ に対して 1 ステップずつ計算するよりも，これらをまとめてやってしまう方がメモリへの再配置等が少なく済みますしパフォーマンスが良くなりました．

実装例（501ms）https://judge.yosupo.jp/submission/203753

これを適当に $1$ 次元配列で省メモリに実装しなおしたところ，次のようになりました．

実装例（477ms）https://judge.yosupo.jp/submission/203754

Power Projection の FFT を利用した高速化 (案2)

本記事ではじめに紹介した実装例では，2 次元の畳み込みを 1 次元の畳み込みに帰着するという方法を紹介しました．

実装例（1042ms）https://judge.yosupo.jp/submission/203746

$2$ 次元配列の $(i,j)$ 成分をインデックス $2nj+i$ 成分に対応させるようにしていれば，必要な操作はやはり，畳み込んだあと偶奇の適切な方を取り出すというものになります．したがってこの実装方針をとった場合でも，FFT の性質を利用した高速化が可能です．

実装例（531ms）https://judge.yosupo.jp/submission/203785

算術演算の回数は (案1) よりも多いはずですが，ボトルネックとなる部分の処理が各反復において長さ $4n, 2n$ の FFT を $2$ 回ずつ呼ぶというだけのシンプルなものになっていて，結果的に (案1) に近い実行時間を達成しています．

実装量の簡潔さとパフォーマンスの良さのどちらもまずまずで，結構良いかも．

コメント

Power Projection のアルゴリズム・実装の基本的な解説はここまでとします．私の力量や時間の都合もあり，Library Checker 最速になるほど洗練された実装を解説することはできませんでしたが，重要な考え方はおおよそ紹介できたのではないかと考えています．

ここからさらに高速化したい場合に考えられる方向性について簡単に述べます．私もすべてを実装してはいません．

  • 型 $(n,m)$ の多項式を長さ $(2n,2m)$ で FFT する際，FFT を行う軸の順序に工夫の余地がある．

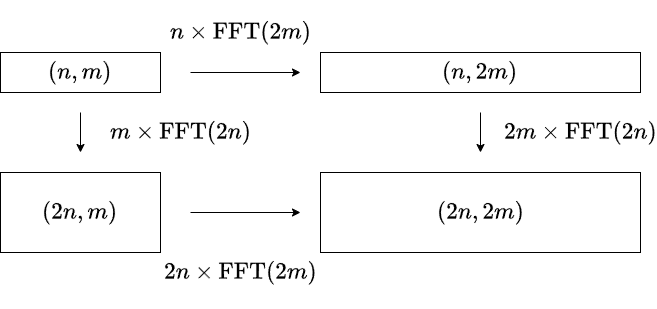
上図の通り，$2$ つの計算方法によって $n\mathrm{FFT}(2m)-m\mathrm{FFT}(2n)$ の計算量の差が生じます．$\mathrm{FFT}(n)$ を $n\log n$ の定数倍と見積もると，長い方向の FFT を先に処理した方が高速になると考えられます（Nachia さんのアイデア）．

  • $2$ 次元配列のすべての列（あるいは $1$ 次元配列を $k$ 個おきに取り出したもの）に対して何かをするという計算が頻発します．FFT の実装をこうした場合に適用できるように一般化しておくと，メモリを移し替える回数が少なくなって，高速化になるかもしれません．
  • この記事で紹介した実装では，$y$ 方向について常にフーリエ変換した値を持っています．さらに $x$ 方向についてもフーリエ変換した値を持つようにするという方針も考えられます．この方法も検討しましたが，私は計算量を落とすことはできませんでした（同程度にはなります）．次のことができれば計算量が改善できると思いますが，難しいと思っています．

長さ $2n$ の列 $(a_0, \ldots, a_{2n-1})$ のフーリエ変換が与えられる．長さ $2n$ の列 $(a_0, \ldots, a_{n-1}, 0, \ldots, 0)$ のフーリエ変換を求めたい．これを $2\times\mathrm{FFT}(2n)$ よりも良い計算量で行うことはできるか？

ここまでいくつかの実装を紹介しましたが，フーリエ変換の性質を上手く使った高速化をしている実装は，多項式の FFT が可能であるという係数環の性質に依存していることにも注意してください．競技プログラミングでの利用を考えている場合には，例えば 「$\mod 998244353$ では使えるが $\mod 1000000007$ では使えない」実装になってしまうということです．最初に紹介した実装のような convolution しか使わないような実装であれば，convolution が可能な係数環でさえあれば利用できるので，その意味ではライブラリの整備は簡単です．

次回 → FPS 合成・逆関数の解説（2）転置原理による合成アルゴリズムの導出

スポンサーリンク
タイトルとURLをコピーしました