For English Readers → FPS Composition and Compositional Inverse (Part 2)
概要
続きです.
前回 → FPS 合成・逆関数の解説(1)逆関数と Power Projection
$f(x), g(x)$ を FPS とするとき,次のどちらかが成り立つ状況で合成 $f(g(x)) = \sum_{i=0}^{\infty}([x^i]f)g(x)^i$ が定義されます.
- $f$ は多項式である.
- $[x^0]g=0$.
本記事では,$f(x), g(x)$ の $n-1$ 次以下の部分が入力されたときに,$f(g(x))$ の $n-1$ 次以下の部分を $\Theta(n\log^2n)$ 時間で求めるアルゴリズムと,ある程度高速に動作する実装を紹介します.
簡単にいうと,前回解説した Power Projection は,合成の転置問題となっており,したがって合成アルゴリズムは Power Projection アルゴリズムの転置をとることで導出できるというものです.したがって転置原理に慣れていれば,今回の記事の内容はすべて自力で簡単に導出できはずです.
この記事の読者層であっても,転置原理を学んだり,それをアルゴリズムの導出に利用したことがない人は多いと思うので,合成アルゴリズムの導出を通して転置原理も学べるような解説を目指しました.
転置原理については集合べき級数の power projection の解説でも扱っており,本記事の何割かの部分はこの記事と完全に同一です.
なお,論文 Power Series Composition in Near-Linear Time では本記事で扱うのと本質的には同じ合成アルゴリズムを転置原理を使わずに説明しているので,合わせて確認してみてください.
参考文献
転置写像と転置原理
転置写像の定義等を完全に理解できなくとも,後述の合成アルゴリズムの導出は理解できるように解説するつもりなので,難しければ飛ばしてください.
転置写像の簡単な説明は「行列で書いたときに転置行列になるやつ」なのですが,私は写像を行列で書くのが苦手なので,線形写像の言葉で一応書いておきます.
転置写像(抽象的な定義,読み飛ばし可)
$K$ を環とし,$M, N$ を自由加群,$F\colon M\longrightarrow N$ を $K$ 線形写像とする.このとき $K$ 線形写像 $F^{T}\colon \mathrm{Hom}_K(N, K) \longrightarrow \mathrm{Hom}_K(M, K)$ が $\phi\mapsto \phi\circ F$ により定まる.これを $F$ の転置写像という.
というのが抽象的な定義です.
転置写像(成分による定義)
$K$ を環とし,$F\colon K^n\longrightarrow K^m$ を $K$ 線形写像とする.$f$ の転置写像 $F^{T}\colon K^m\longrightarrow K^n$ とは,次によって一意に定義される線形写像である.
- $(x_1, \ldots, x_m)\in K^m$ とする.$f_1, \ldots, f_n \in K^n$ に対して $(g_1, \ldots, g_m) = F(f_1, \ldots, f_n)$ としたとき,$\sum_jx_jg_j = \sum_iy_if_i$ が任意の $(f_i)$ に対して成り立つような $(y_1, \ldots, y_n)$ が一意に存在する.これを $F^{T}(x_1, \ldots, x_m)$ と定める.
よって,「$F^{T}(x_1, \ldots, x_m)$ を計算せよ」という問題は「$\sum_j x_jg_j$ という式を $\sum_i y_if_i$ と表せ」と考えることができます.「$\sum_j x_jg_j$ という式における各 $f_i$ の寄与を求めよ」と考えてもよいでしょう.
なお,$F$ と $F^T$ では始域と終域が入れ変わっていますが,逆写像というのとは全然違うので注意してください.
転置原理
転置原理とは大雑把にいえば,次の $2$ つの問題が同程度の計算量のアルゴリズムを持つというものです:
- $f = (f_1, \ldots, f_n)$ を入力として $F(f) = (g_1, \ldots, g_m)$ を出力する問題
- $x=(x_1, \ldots, x_m)$ を入力として $F^{T}(x) = (y_1, \ldots, y_n)$ を出力する問題
$F$ のアルゴリズムから $F^{T}$ を導出することは, $F$ のアルゴリズムの算術演算を全て列挙していけば原理的にはできるはずですが,アルゴリズムが複雑だとそのような方法での機械的なアルゴリズム導出は大変です.実際には,算術演算単位ではなくもう少し大きなステップのアルゴリズムに分解して,各ステップの転置問題を(転置原理を用いずに)解くことで導出することが多いと思います.本記事でもそのような手順で,合成のアルゴリズムを導出します.
Power Projection の転置と合成
まずは,「Power Projection の転置は合成である」ということを説明します.
Power Projection を再掲します.前回記事と比べて使う記号を変えたりしています.また列や FPS の長さは省略しますが,すべて $n$ であるとしてください.
[Power Projection] 列 $w=(w_j)$ と FPS $g(x)$ が与えられる.各 $i$ に対して $\mathrm{PowProj}(w,g)[i] := \sum_{j}w_j[x^j]g(x)^i$ を求めよ.
この問題の転置を考えましょう.というのは本当は少し正確ではありません.転置は線形写像に対して定義されるものですが,写像 $(w,g)\mapsto \mathrm{PowProj}(w,g)$ は線形写像ではありません.
一方で $g$ が固定して,写像 $\mathrm{P}_g = \mathrm{PowProj}(-,g); w\mapsto \mathrm{PowProj}(w,g)$ を考えるとこれは線形写像です.そこで,$\mathrm{P}_g$ の転置 $\mathrm{P}_g^T$ がどのような写像かを考えましょう.
転置写像の成分による定義を踏まえると,$f=(f_0,\ldots,f_{n-1})$ に対して,$(x_0,\ldots,x_{n-1}) = \mathrm{P}_g^T(f)$ は,任意の $w$ に対して $\sum_{j}w_jx_j = \sum_i f_i\mathrm{P}_g(w)[i]$ を満たす列です.つまり 「$\mathrm{P}_g(w)$ を求めよ」の転置問題「$\mathrm{P}_g^T(f)$ を求めよ」は次のように定式化できます.
[Power Projection の転置] $f,g$ が与えられる.列 $w$ に対して $X = \sum_i f_i \mathrm{P}_g(w)[i]$ という値を考える.これを $\sum_{j}w_jx_j$ と表したときの $(x_0,\ldots,x_{n-1})$ を求めよ.
$\mathrm{P}_g(w)=\mathrm{PowProj}(w,g)$ の定義を思い出すと,
$$X = \sum_if_i\sum_jw_j[x^j]g(x)^i = \sum_jw_j[x^j]\sum_if_ig(x)^i$$
よりこの問題の解は明らかに $x_j=[x^j]\sum_if_ig(x)^i=[x^j]f(g(x))$ です.以上により Power Projection と合成,より正確には $g$ を固定したときの $w\mapsto \mathrm{PowProj}(w,g)$ と合成 $f\mapsto f(g(x))$ が転置の関係にあることが分かりました.
したがって転置原理によれば,合成に Power Projection と同程度の計算量のアルゴリズムが存在することが言えます.以下ではそのアルゴリズムが具体的にどのようなものであるかを考えていきます.
Power Projection 転置アルゴリズム(全体像)
Power Projection のアルゴリズムをおおよそ理解していることを前提とします.これを次の図のように表しておきます.

Power Projection 転置問題は,$f,g$ が入力されたときに $X = \sum_i f_i \mathrm{P}_g(w)[i]$ という量を $w$ で表したときの係数を求めよというものです.$X$ を計算するステップも付け足して考えると理解しやすいと思います.

解くべき問題は,「$f,g$ が与えられたときに $X$ を $w$ で表せ」です.上図のうち,解くときに与えられるものとそうでないものを意識することは重要です.

上図のうち $f, g$ は与えられ,$Q_i$ は $g$ から計算可能なので,上図のうち赤文字で与えられる量はすべて与えられていると思ってよいです.それ以外のものはすべて $w$ を与えると順に計算される量です(より詳しくは,「与えられる量」から定まる線形写像によってうつすという計算です).
これを次の手順によって計算します.
- $X$ は output の係数 $f_i$ の線形結合であることが分かっている.
- それを利用して,$X$ を $P_k$ の要素の線形結合で表したときの係数を求める.
- $\vdots$
- それを利用して,$X$ を $P_0$ の要素の線形結合で表したときの係数を求める.
- それを利用して,$X$ を $w$ の要素の線形結合で表したときの係数を求める.
このように元の問題の逆の手順で計算します(行列積の転置に関する性質 $(A_1\cdots A_n)^T=A_n^T\cdots A_1^T$ に対応します).
これまでのことをまとめると,合成のアルゴリズムの全体像は次の図のように表すことができます.

まず,$g$ から $Q_0, Q_1, \cdots$ を計算します.これは Power Projection アルゴリズムと完全に同じ計算をすることになります.
次に,何らかの量 $X$ を $P_i$ の要素の線形結合で表したときの係数 $p_i$ を後ろから順に求めていきます.この計算を繰り返すと最終的に $X$ を $w$ の要素の線形結合で表したときの係数が得られ,これが求めたかったもの $f(g(x))$ になります.
Power Projection 転置アルゴリズム(実装例)
説明を簡単にするため,$[x^0]g=0$ を仮定し,$n$ が $2$ のべき乗であるとします.
転置アルゴリズムを実装するには,もとのアルゴリズムの実装をまず用意します.
上で説明したように,「$g$ から $Q_i$ を順に求める反復を行ったあと,その結果に基づいて後ろから戻ってくる」という計算の流れになります.したがって再帰関数を使って実装しておくと簡潔になります.また,Power Projection のときと違って,$Q_i$ の値を $Q_{i+1}$ 計算後にも再使用することになるので,同じ配列を上書きして使いまわすことを避けた実装をしておきます.
これを踏まえて次の実装を用意しました(利用しているテンプレ等の情報が必要であれば 提出 から拾ってください).
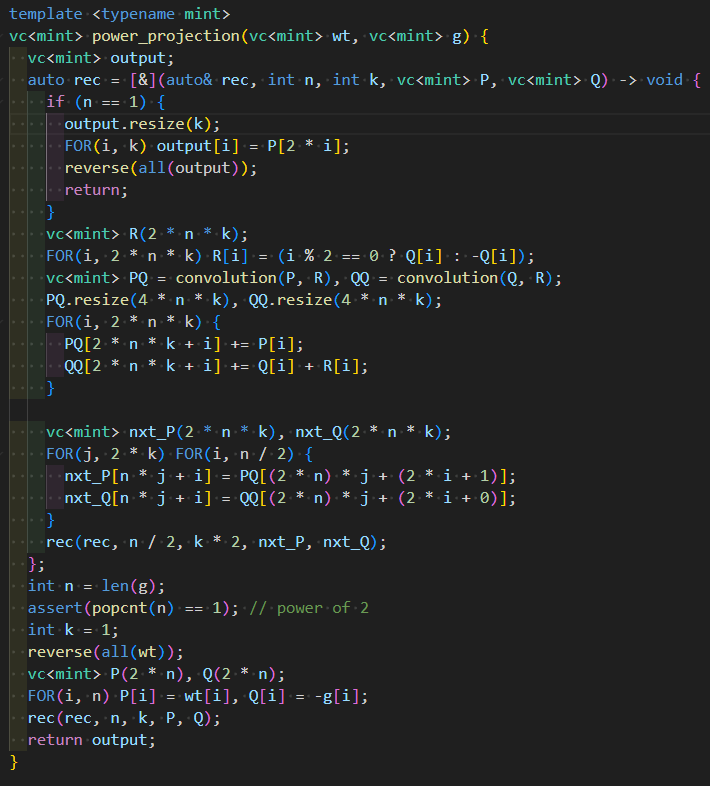
さらにこれを $Q$ に対する計算と $P$ に対する計算に分離しておくと分かりやすいです.
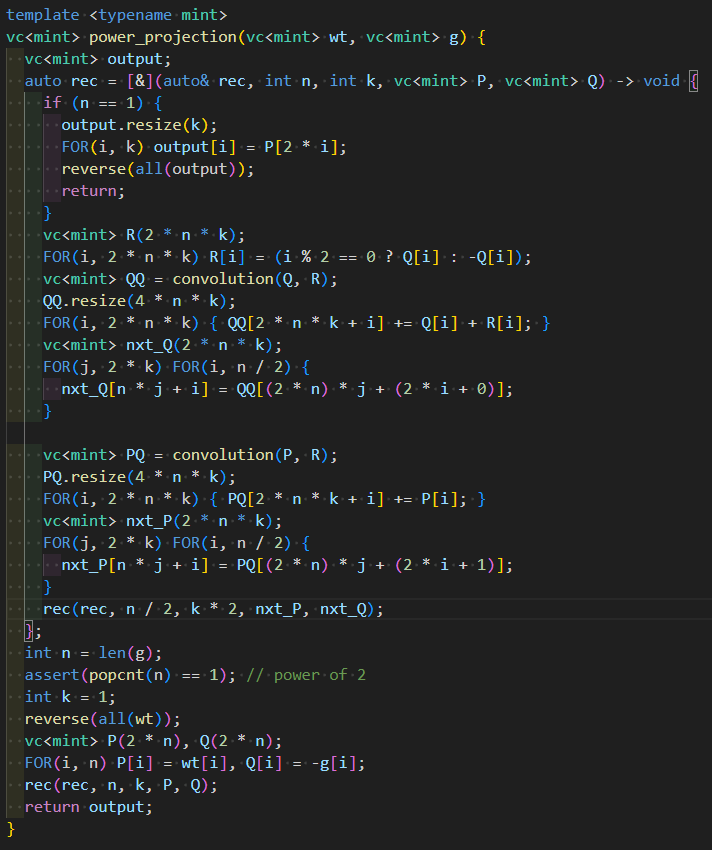
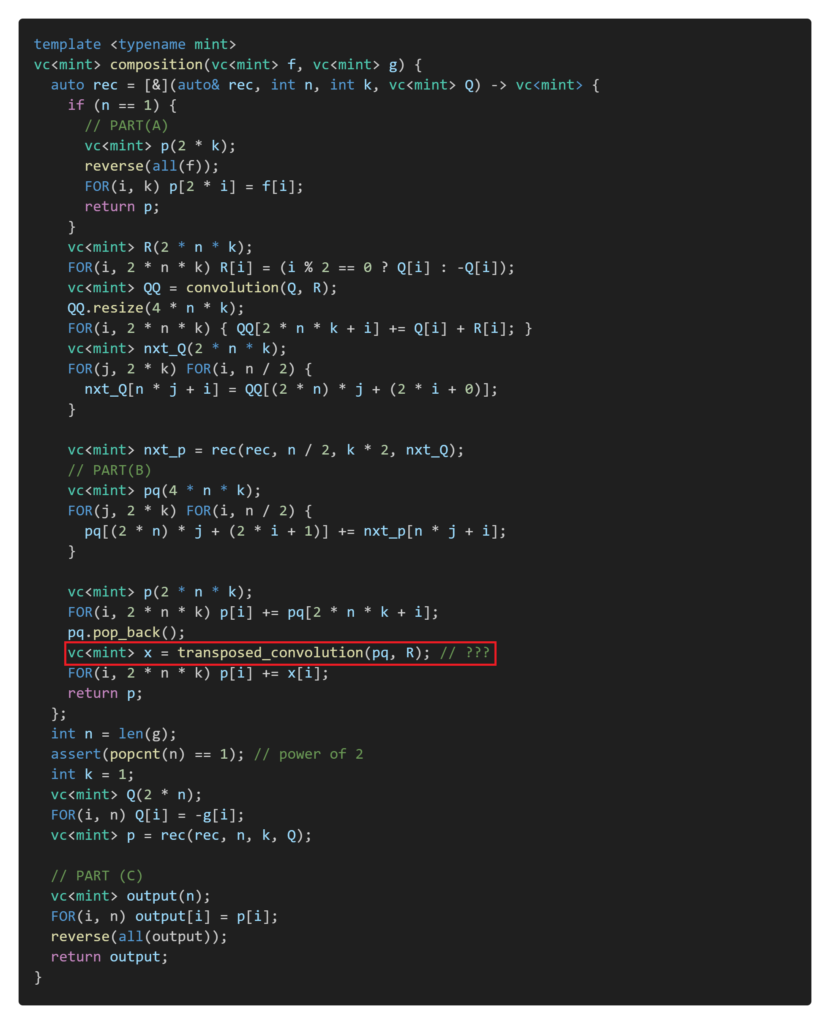
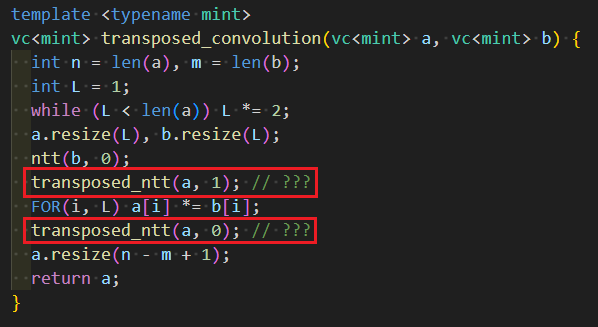
これを変更して,合成の実装になるようにしましょう.「P から nxt_P を求める」といった実装を,「nxt_P の係数から P の係数を求める」といった実装に置き換えます.だいたい次のような実装をすればよいことになります.
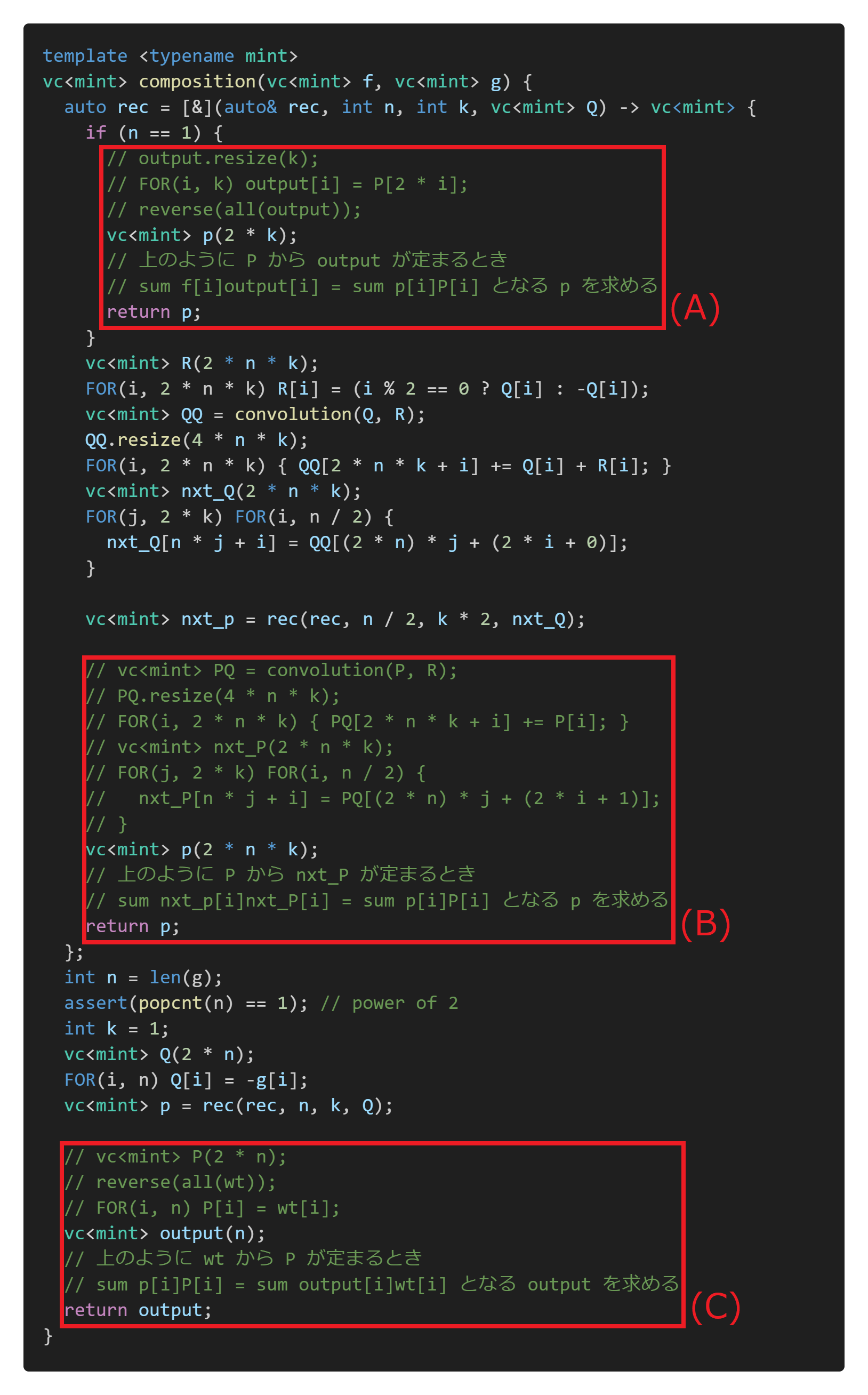
赤枠で囲った場所が 3 つあり,ここを適切な実装に取り換えれば合成の実装の完成ということになります.それぞれアルゴリズム全体像の図のうち次の部分に対応しています.
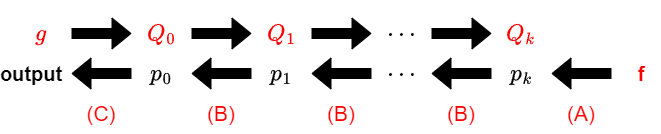
さて,(A), (C) は簡単で,実装すべきものが正しく理解できていればすぐに実装できると思います.このように配列の対応するインデックスに詰めなおしているだけの部分は,対応する場所に入れなおし他は $0$ 埋めして返せばよいです.
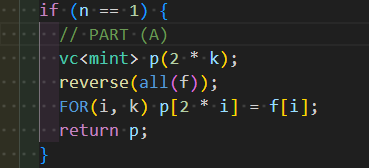
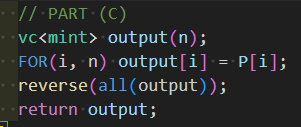
最後に (B) 部分について考えます.転置がどうなるかすぐに分からないときには,いくつかのステップずつに分解して考えましょう.ここは「P から PQ を定める」「PQ から nxt_P を定める」という 2 ステップで実装されています.これを逆順に遡るように実装します.
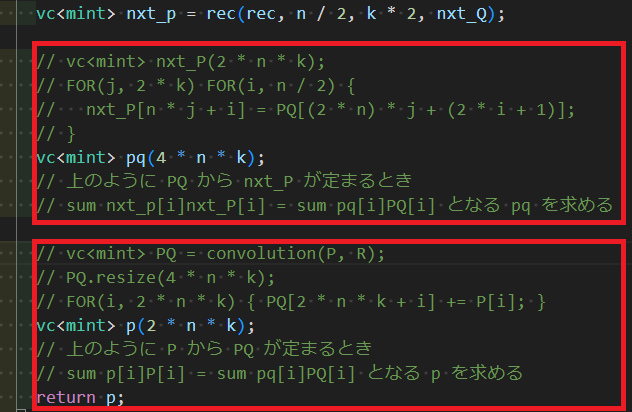
上半分は簡単です.下半分について見ましょう.すると,「$\mathrm{convolution}(-,R)$ の転置で pq をうつす」という処理が必要になることが分かります.とりあえずここは難しいのであとで実装することにしておいて,convolution の転置を除いて次で実装が完成です.
convolution の転置 (middle product)
convolution の転置 (middle product)
$a$ を長さ $n$ の列とし,$b$ を長さ $m$ の列とします.このとき $c = \mathrm{convolution}(a,b)$ は $c_k=\sum_{i+j=k}a_ib_j$ により定まる長さ $n+m-1$ の列です.
$b$ を固定すると,$\mathrm{convolution}(-,b); a\mapsto \mathrm{convolution}(a,b)$ は長さ $n$ の列を長さ $n+m-1$ の列にうつす線形写像です.この写像の転置写像がどのようなものであるかを考えましょう.
これは,長さ $n+m-1$ の列 $x$ を $\sum_{k}c_kx_k = \sum_{i}a_iy_i$ を満たす列 $y$ にうつすような写像です.$c_k = \sum_{i+j=k}a_ib_j$ を代入すると左辺は $\sum_{i}\sum_ja_ib_jx_{i+j}=\sum_i a_i(\sum_jb_jx_{i+j})$ なので,転置問題は次のようになります:
長さ $n+m-1$ の列 $x$ が与えられたとき,$y_i=\sum_jb_jx_{i+j}$ により定まる長さ $n$ の列 $y$ を求めよ.
この列 $y$ は $x, b$ の middle product とも呼ばれます(参考記事内「middle product」).
畳み込みに慣れている読者であれば,これは畳み込みを用いて簡単に計算できることに気付くと思います.$b,x$ のどちらかを reverse して畳み込んだあと,適切な値をあつめて出力すればよいです.これをそのまま実装すると,長さ $n+2m$ 程度の FFT が必要となります.
しかし middle product は適切に実装すると長さ $n+m-1$ 程度の FFT だけでより高速な実装が可能です.以下ではこの方法を $2$ 通りの方法で解説します.
なお,middle product は転置問題を考えるとき以外でもしばしば利用可能です.気づかずに普通の畳み込みを行っている人も多いと思います.
middle product の計算 (導出1)
$b$ を reverse すれば,求めたいものは $y_i=\sum_{j}x_{i+j}b_{m-1-j}=\sum_{j+k=m+i-1}x_jb_k$ となります.したがって $x, b$ を畳み込んだあと $m-1$ 番目から $m+n-2$ 番目を取り出せばよいです.
畳み込んだあと必要な部分が少ないことを利用すると,畳み込みを巡回畳み込みに取り換えることができます.つまり,$L\geq n+m-1$ を満たす $L$ をとり $x,b$ を長さ $L$ の巡回畳み込みをしたあと $m-1$ 番目から $m+n-2$ 番目を取り出せばよいです.
実際,$0\leq j< n+m-1$ および $0\leq k<m$ に対して $0\leq j+k<n+2m-1\leq L+m$ なので,巡回畳み込みで $m-1$ 番目から $m+n-2$ 番目に入ってくる項は通常の畳み込みでもその範囲に入ってくる項しかないことが分かります.
middle product の計算(導出2)
middle product が convolution の転置であったことに注意して,転置原理からアルゴリズムを導出してみましょう.
convolution は次の計算手順で計算できるのでした.
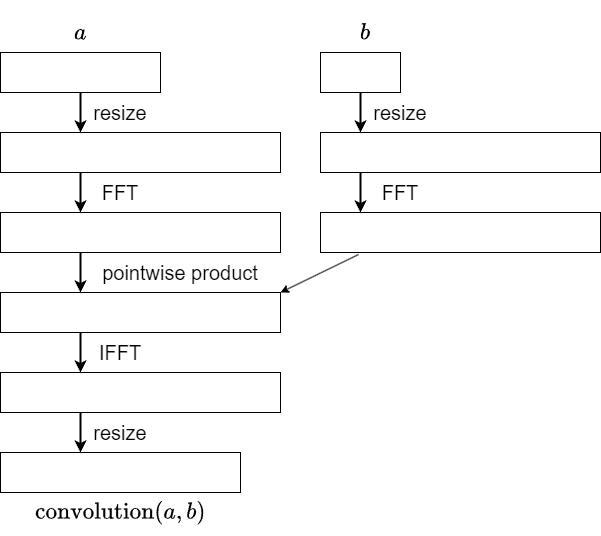
転置を考える際,$b$ を定数と見なしていたことに注意してください.$a$ から $\mathrm{convolution}(a,b)$ を得る操作が,($b$ から定まる)線形写像 $5$ つの合成として表されています.転置写像は,各ステップを逆向きに辿るという $5$ つの合成として表せることになります.
pointwise product については,$b$ を定数と見なしていたことを思い出すと,成分ごとの定数倍ということになります.よって転置も同じ定数倍です.よって次のような実装が可能だと分かります.
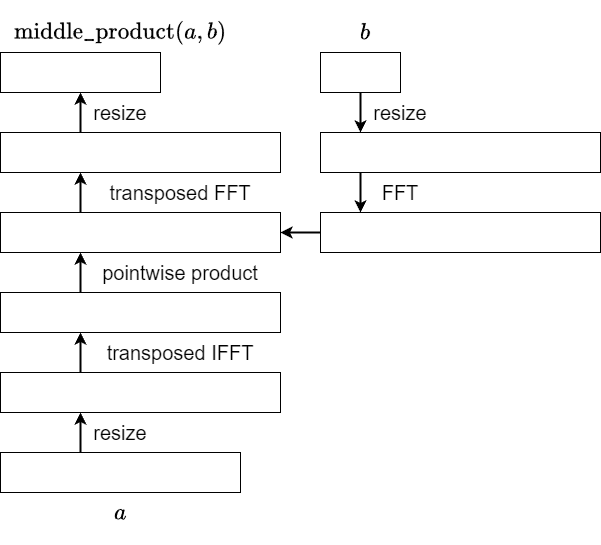
あとは FFT, IFFT の転置がどのようなものかが分かればよいことになります.これはこれで,利用先が middle_product に限定されない重要な問題なので,改めて次で説明します.
フーリエ変換の転置
$a$ を長さ $n$ の列とし,$1$ の原始 $n$ 乗根 $\omega$ を固定するとき,$\mathcal{F}[a]_i=\sum_{j}\omega^{-ij}a_j$ により定まる列 $\mathcal{F}[a]$ を $a$ のフーリエ変換というのでした.フーリエ変換は対称行列をかける操作としてかけており,フーリエ変換の転置はフーリエ変換そのものであることが分かります.
逆フーリエ変換は $\mathcal{F}^{-1}[a]_i = \dfrac{1}{n}\sum_j\omega^{ij}a_j$ により定義され,フーリエ変換の逆変換になります.これも対称行列をかける操作としてかけているので,逆フーリエ変換の転置は逆フーリエ変換そのものです.
なお,これらの定義は(どちらに $1/n$ をつけるか等)少し違った定義を採用している文献も多いので注意してください.
というわけで,(逆)フーリエ変換の転置がどのようなものか分かりました.完.
というのでおおよそ正しいのですが,注意点もあります.
フーリエ変換を bit 反転順に並べた列を出力する FFT の実装が,現在広く使われています(例えば AtCoder Library). そのため,FFT の実装によってはそのものが自身の転置になるとは限りません.
bit reversed FFT の転置
$n=2^k$ を $2$ のべき乗とし,$\mathrm{rev}(i)$ を $i$ の $2$ 進法 $k$ 桁目までの bit 反転とします.bit reversed FFT, bit reversed IFFT を次で定義します(より正確には FFT は変換の呼称というよりはそれを高速に行う方法を指しますが,多めに見てください).
- bit reversed FFT:列 $a$ を入力し,$b_i = \sum_j \omega^{-\mathrm{rev}(i)\cdot j}a_j$ により定まる列 $b$ を出力する.
- bit reversed IFFT:列 $b$ を入力し,$a_i = \dfrac{1}{n}\sum_{j} \omega^{i\cdot \mathrm{rev}(j)}b_j$ により定まる列 $a$ を出力する.
したがってこれらの転置は次のような変換です:
- transposed bit reversed FFT:列 $b$ を入力し,$a_i = \sum_j \omega^{-i\cdot \mathrm{rev}(j)}b_j$ により定まる列 $a$ を出力する.
- transposed bit reversed IFFT:列 $a$ を入力し,$b_i = \dfrac{1}{n}\sum_j \omega^{\mathrm{rev}(i)\cdot j}a_j$ により定まる列 $b$ を出力する.
見比べると,「bit reversed FFT と transposed bit reversed IFFT」「bit reversed IFFT と transposed bit reversed FFT」がそっくりであることが分かるでしょう.これらの違いは全体にかかっている $\dfrac{1}{n}$ と指数の $-1$ 倍だけなので,次の結論が得られます:
- transposed bit reversed FFT は,bit reversed IFFT でうつしたものを先頭以外 reverse して $n$ 倍したものである.
- transposed bit reversed IFFT は,先頭以外を reverse したものを bit reversed FFT したものの $1/n$ 倍である.
「先頭以外を reverse」という操作が現れるのは,$\omega^{-i} = \omega^{n-i}$ から $i$ 番目を $n-i$ 番目にうつしているからです.
合成の実装例(完成版)
長くなりましたが,ここまでの議論で合成の実装は完成しています.次の実装は本記事の説明通りに実装しています.
実装例(1035ms)https://judge.yosupo.jp/submission/204008
元にした Power Projection の実装 (逆関数, 1042ms)とだいたい同じくらいの実行時間になっています(逆関数の方が,Power Projection の後に形式的べき級数の pow を計算している分すこし実行が遅いです).
なお,本記事では説明を簡単にするために $n$ が $2$ べきであることや,$[x^0]g=0$ などを仮定した実装を紹介したので,自身のライブラリに反映させる場合にはこれらの点に注意してください.
本記事では,Power Projection の実装例をひとつ選び,転置原理を適用することで合成の実装を行いました.もちろんより計算量の良い Power Projection の実装からはじめれば,さらに高速な合成の実装が得られます.例えば 前回の記事で (案2) として紹介した実装(逆関数, 531ms) からは,実装例(479ms) が得られました.転置原理の練習として挑戦してみてください.

