概要
特に別解ではないですが、想定解の正当性の保証が大変だったので、書きます。
かなり一直線に解ける問題で、難しい部分は少ない。ように見えますが…。
計算精度の問題
「最小のもの」を見つけるのが問題です。解説では比較関数 $\log(A_i+A_j)+A_j\log A_i$ を用いて計算することが書かれています。
数学の計算式としては正しいのですが、計算誤差の問題はないでしょうか?いくら実数として順序が定まっていても、コンピュータはそれを完全な精度で扱うことができません。
例えば小数を扱う形式として広く用いられるもののひとつに、64bit 浮動小数点数がありますが、これは約 $16$ 桁程度の有効数字しか持ちません(wikipedia 倍精度浮動小数点数)。それ以上の桁数を計算しようとすると、多くの言語では、やや特殊な小数型が必要とされたり、計算時間が多く必要になったりします。
競プロの文脈では、例えば、$1\leqq a,b,c,d\leqq 10^9$ という制約のときに、小数計算で $\frac{a}{b}$ と $\frac{c}{d}$ の順序を検出することは、64 bit 浮動小数点数では失敗します。($1\leq a,b,c,d\leq 10^5$ であれば、異なる有理数に対して $\bigl\lvert\frac{a}{b} – \frac{c}{d}\bigr\rvert \geq \frac{1}{bd} \geq 10^{-10}$ などとなって、$16$ 桁の有効数字があれば十分対応できます。)
今回は、$\log(a+b) + b\log a$ と $\log(c+d) + d\log c$ の比較です。対数の線形結合については、 Bakerの定理 などがありますが、今回の問題について見ればあまりに弱い下界しか与えられないです(具体的に計算可能な下界を与えただけでもとてもすごくて、フィールズ賞を受けている定理です)。
試しに計算してみると、次のような例も見つかります。
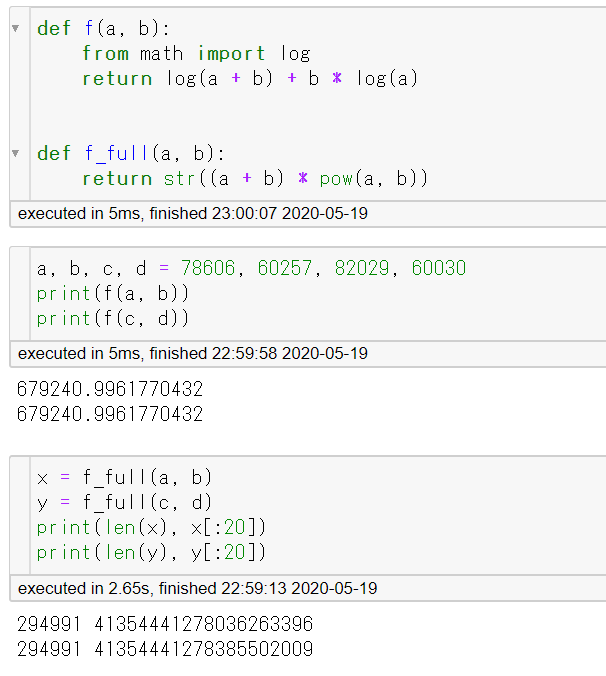
解説の通りの比較関数ですが、有効数字 $16$ 桁分、完全に一致しています。多倍長整数を使って完全な精度で整数計算すると、$(a+b)a^b$ と $(c+d)c^d$ は、ともに $294991$ 桁で、最上位 $11$ 桁までが一致していることが確認できます。
$11$桁しか合わないの?$16$ 桁じゃなくて? と思うかもしれませんが、巨大な数 $x, y$ が何桁目まで一致するかは、$\log x$, $\log y$ の小数部分の差(相対誤差ではなく絶対誤差)が影響します。今回は $\log x$ の整数部分が $679240$ と大きいので、有効数字 $16$ 桁を計算しても小数第 $10$ 位程度までしか計算できていないところでこのような結果になります。
本問の正当性
以上を踏まえて、私はまず、想定解が「嘘解法」だろうと予想をしました。ほとんどの提出が誤答になるようなテストケースが存在するだろう、もしかすると与えられた制約、実行時間での正しい解法は困難かもしれない、と。
そしてさらに検証を進めるうちに、(残念ながら?幸運なことに?)この問題の解法としては $\log$ を用いた比較による解法が正当であることが発覚します。以下に、その検証を述べます。
上記のように、比較関数 $\log(a+b) + b\log a$ で区別困難なパラメータ $(a,b,c,d)$ は多数存在します。しかしながら本問題の特徴として、完全なソートを要求していません。最小値の特定だけが要求されています。
以下、$f(a,b) = (a+b)a^b$ とおきます。$f$ の最小値を与える可能性がある組 $(A_i, A_j)$ 同士だけが、$\log$ を使った比較関数で区別できれば十分です。最小値を与える可能性がある組を、どんどん限定していきましょう。性質 $a_1 < a_2\implies f(a_1,b)<f(a_2,b)$, $b_1<b_2\implies f(a,b_1)<f(a,b_2)$ を用います。
まず、$(A_i, A_j)$ のうち、$A_i = \min\{A_1,\ldots, A_{j-1}\}$ が成り立たないものは候補から外してよいです。また $j$ に対してこのような $i$ が複数あるときは、最小の $i$ のみを候補として考えることにします。
$(A_i,A_j)$ と $(A_k, A_l)$ が最小値の候補であるとしましょう。さらに、$j<l$ を仮定しておきます。
まず $j < k$ とします。$(A_k,A_l)$ が候補であることから、$A_k < A_i, A_j$ が成り立ちます。すると、$f(A_i,A_j) > f(A_i, A_k)$ が成り立つので、$(A_i, A_j)$ を最小値の候補から外すことができます。よって $j < k$ であるような組 $(A_i,A_j), (A_k, A_l)$ は比較する必要がありません。
今度は $i < k < j$ とします。この場合は、組 $(A_k, A_l)$ から $A_k < A_i$ が導けて、$(A_i, A_j)$ が候補になっていることに矛盾します。
結局、比較すべき組 $(A_i,A_j), (A_k,A_l)$ は、$k\in \{i,j\}$ を満たすものしか存在しないことが分かります。$i=k$ ならば、やはり比較は自明です。残ったのは $A_j = A_k$ の場合です。つまり、$1\leqq a,b,c\leqq 10^5$ のもとで、組 $(a,b)$ と組 $(b,c)$ を比べることができればよいです。
これが $64$ bit 浮動小数点数の範囲で十分区別できることは、全探索により確かめられます(すべての $(a,b)$:$10^{10}$ 通りに対して、値が近くなる $c$ を二分探索する方法で調査しました)。
以上により、比較関数 $f(a,b) = \log(a+b)+b\log a$ を用いた解は、この問題の制約で常に正答を出力することを確かめることができました。

