概要
どのくらい他の方と、最終的にできるものが違うのか分かっていないですが…。
解法
$A_i$、$B_j$ はソートしておく。LISの長さはコントロールしにくいので、どの行・列についても、$$C_1 < C_2 < \cdots < C_n > C_{n+1} > \cdots$$を作ることを目指します。
1列目あるいは1行目から順に、割り当てを確定できます。
(1)$A_1 \geqq 2$(どの列も、LIS $2$ 以上を目指す)のとき
盤面に割り当てるべき数のうち、最小のもの $W$ 個を、それっぽく配置します。2行目以降で、$B_i$ を $1$ ずつ減らした場合の問題を解くことに帰着されます。

例えば $B = (2,2,3,4,4,6)$ ならば、$B = (1,1,2,3,3,5)$ として次の行に進みます。
(2)$B_1 \geqq 2$(どの行も、LIS $2$ 以上を目指す)のとき
(1)と同じことをすればよいです。
(3)$A_1 = B_1 = 1$ のとき
あとはこの場合の戦略が確定できれば解決です。$B_i = 1$ の列と $B_i \geqq 2$ の列に分けて、割り当てるべき数の最大値付近、最小値付近を単調減少に並べます。
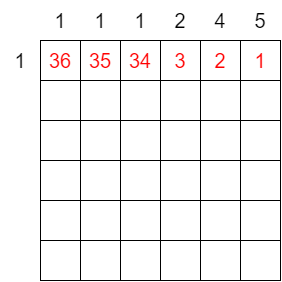
$B_i = 1$ のところは $B_i = 1$ のままにして、次の行に進むとちょうどよいです。
サンプル
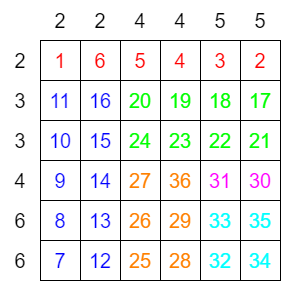
行方向に埋めたり列方向に埋めたり切り替えながら再帰的に作っていきます。(numpy.ndarrayを転置しながら行方向にのみ埋めるような実装をしました。)

