概要
解いたユーザー数が少なく、レベル評価も高い問題です。が、それほど難しくないと感じてしまった。色んな人が取り組めば、結構簡単にいろんな解法が出てきそうな気もします。
解説で書かれていた方法とは違っていたので、書きます。
そういえば、想定解法が $\Theta(N^2\log N)$ でしたが、私の解法は $\Theta(N)$ になっています。
主な戦略
とりあえず、2 種類距離がありますが、大変なので、どちらか片方に専念できる仕組みを用意しましょう。距離 $20$ のペアを、$1$ つずつ増減させられるような構図を考えます。
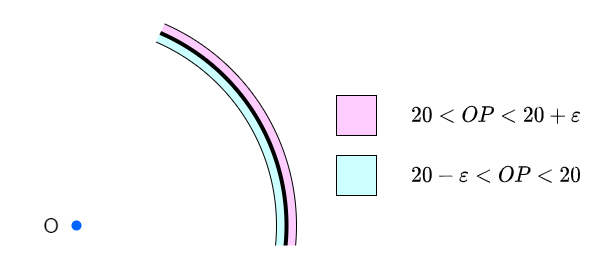
$1$ 点 $O$ を適当にとります(例えば原点)。非常に小さな正の実数 $\varepsilon$ をとって、半径 $20$ の円周を考えます。ここの円周上で「距離 $10$ 未満のペアを指定個数つくる問題」を解いたあと、円周上に並べた各頂点を$O$ を中心に $1 \pm \frac{\varepsilon}{20}$ 倍拡大で出し入れすることで、距離 $20$ のペア数が $1$ つずつ調整できます。また、円周のうち中心角 $60^{\circ}$ 部分しか使わないようにすれば、距離 $10$ の問題を考える際に距離 $20$ の条件を完全に忘れることができます。
…これだとまだ不完全ですね。距離 $20$ のペアを $1$ つずつ調整できるとはいえ、調整可能なのは使う点の個数までですから、$\frac{N(N-1)}{2} – (N-1) \leq B\leq \frac{N(N-1)}{2}$ の範囲にしか対応できないようにも見えます。
しかしこれは対応が簡単で、$B$ があまり大きくないときは、いくつかの点を距離 $20$ 以下のペアができないようにして遠方に捨ててしまえば、やはり $\frac{N(N-1)}{2} – (N-1) \leq B\leq \frac{N(N-1)}{2}$ の問題に帰着できます($N$ を減らしても $A$ の範囲の条件は保たれます)。
というわけで、解法の概要は以下の通りです。
(1) $\frac{N_0(N_0-1)}{2} – (N_0-1) < B \leqq \frac{N_0(N_0 – 1)}{2}$ となる $N_0$ をとる。
(2) $N – N_0$ 個の頂点は遠くに距離 $20$ のペアができないように捨てる。
(3) $1$ 点 $O$ を適当にとる。残り $N_0 – 1$ の頂点を適切に円弧上に並べて、これらの点同士の距離は全て $20$ 未満であり、距離 $10$ 未満のペアは $A$ 個になるようにする。
(4) $N_0 – 1$ 個の頂点を $O$ を中心に $1\pm \frac{\varepsilon}{20}$ 倍に拡大することで、距離 $20$ 未満のペアが $B$ 個になるように調整する。(1) の範囲に $N_0$ をとっているのでこれは可能。
という作りです。より正確には、(4) の拡大で (3) で作ったペアの個数が変わらないようにするため、(3) では全ての $2$ 点間の距離を $9.9$ 未満または $10.1$ 以上 $19.9$ 以下にする($10$, $20$ にとても近い距離は避ける)ことで、(4) で正の実数 $\varepsilon$ をとることができます。
距離 10 未満のペア数の調整
円弧上の $2$ 点の距離は中心角から定まるため、上記 (3) の問題は本質的には $1$ 次元(数直線)の問題と思うことができます。「距離 $10$」に相当する中心角は、「距離 $20$」の相当する中心角のちょうど半分ではないので少し注意が必要ですが、ほとんど同様なので、以下では数直線での問題に置き換えて説明します。
円周上に $N_0 – 1$ 個の頂点を並べて、距離 $10$ 未満のペアが $A$ 個になるようにしましょう。狭い領域なので、距離 $10$ 未満のペアがとても少ない(例えば $0$ 個)配置は困難に思えますが、ここに制約 $\frac{N_0(N_0-1)}{4} \leqq A\leqq B – N_0$ が利いてきます。
$X = \bigl\lfloor\frac{N_0-1}{2}\bigr\rfloor$ とし、$N_0 – 1 = X + Y$ とします。このとき、$\binom{X}{2} + \binom{Y}{2} \leqq A \leqq \binom{N_0-1}{2}$ が確認できます。この間を連続に補完できればよいです。
これは、例えば次のようにして達成できます。
・$X$ 個の頂点をある点 $P$ から距離 $1$ 以内に、少しずつ離しておいておく。
・$P$ からの距離が $8$ 以上 $12$ 以下の範囲に、$Y$ 個の頂点を置く。
・$Y$ 個の頂点を全て距離 $8$ のところにおくと $\binom{X+Y}{2}$ 個のペア、全て距離 $12$ 個のところにおくと $\binom{X}{2} + \binom{Y}{2}$ 個のペアが実現されるので、この範囲で調整すれば条件が達成できる。
いくつペアが足りていないかを計算しながら、$X$ の点を狙った個数ずつペアに取り込めるので、調整は簡単です。
コメント
作った図形を図示しようと思ったが、完全に同じ座標に複数点を置いていたりして見栄えがいまいちっぽいのでやめ。
作問者の距離 $20$ 未満の調整も面白かったです。こちらも根本的には、距離 $10$ の方をいい感じにしたあと $1$ ペアずつ調整できる仕組みを使っていますね。

