概要
凸関数の凸共役(Legendre-Fenchel 変換)とその性質について、軽くまとめます。さらに、slope trick による凸関数の取り扱いと組み合わせることで、slope trick の凸共役 という新たな凸関数の取り扱いを導出します。呼称はこの記事が初出で、どういう名前が流行るのかは現時点では不明。
凸関数の凸共役
定義
$f\colon \R\longrightarrow \R\cup\{\infty\}$ (ただし恒等的には $\infty$ ではない)とします。$f$ の 凸共役 $f^{\star}$ を次の式により定義します:
$$f^{\star}(p) := \sup_{x} (px-f(x))$$
$f$ から $f^{\star}$ を得る操作は、Legendre-Fenchel 変換 とも呼ばれます。$f^{\star}(p)$ を考えることは、図形的には $f$ のグラフの下側に来るような傾き $p$ の直線のうちなるべく $y$ 切片が大きいものを考えることに対応します。
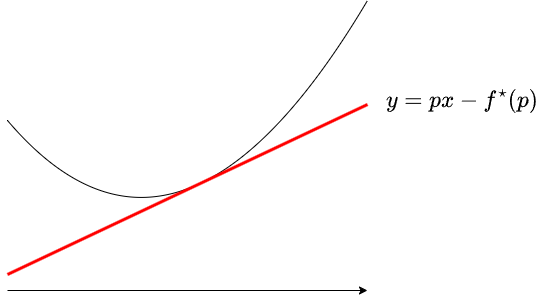
Fenchel の双共役定理
次が成り立ちます。
- $f^{\star}$ は凸関数である
- $f$ が凸関数で、適当な条件を満たすならば、$f = (f^{\star})^{\star}$ が成り立つ
- 「条件」についてはここでは省略しますが、以下に述べる、閉区間上の区分線形凸関数はこの条件を満たします
$f^{\star}$ の凸性は、$f^{\star}$ が線形関数(したがって凸関数)の $\sup$ であることから分かります。$f = (f^{\star})^{\star}$ については、$f \geq (f^{\star})^{\star}$ が定義から直接分かる自明な不等式です(確かめてみてください)。逆側の不等式は、図形的には凸関数のグラフがその 包絡線 全体から復元できることを意味しています。
極小畳み込み(infimal convolution / min plus convolution)
以下、$f,g$ などと書けば「適切な条件」を満たす凸関数だとします。
$f,g$ の 極小畳み込み $f \mathop{\Box} g$ を以下のように定義します:
$$\bigl(f\mathop{\Box} g\bigr)(x) = \inf_{y}\bigl(f(x-y)+g(y)\bigr)$$
凸共役との関係として、次が成り立ちます:
- $\bigl(f\mathop{\Box} g\bigr)^{\star}(p) = f^{\star}(p) + g^{\star}(p)$
- $\bigl(f + g\bigr)^{\star}(p) = (f^{\star} \mathop{\Box} g^{\star})(p)$
つまり、凸共役をとると、加法と畳み込みが入れ替わります。
簡単に証明を述べます。凸共役の性質 $(f^{\star})^{\star} = f$ より上の式のみ示せばよいです。
$$\begin{align*}\bigl(f\mathop{\Box} g\bigr)^{\star}(p) &= \sup_x\bigl(px {}-{} f\mathop{\Box}g(x)\bigr) = \sup_{x,y}\bigl(px-f(x-y)-g(y)\bigr) \\&= \sup_{x,y}\bigl(\bigl(p(x-y)-f(x-y)\bigr) + \bigl(py-g(y)\bigr)\bigr) \\&= \sup_{x,y}\bigl(\bigl(px-f(x)\bigr)+\bigl(py-g(y)\bigr)\bigr) = f^{\star}(p)+g^{\star}(p)\end{align*}$$
区分線形凸関数の凸共役
slope trick (1) 解説編 で解説した形の区分線形凸関数 $f$ に対して、$f^{\star}$ もやはり区分線形凸になり、そのグラフには次のような関係があります。
- $f$ が、$x = a$ の前後で傾き $b$ から傾き $c$ に変化するとき、$f^{\star}$ は $[b,c]$ 上で傾き $a$ である
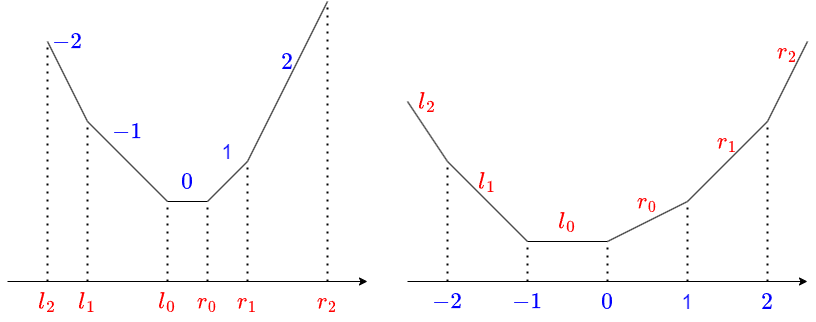
$p\in [b,c]$ に対して、$f$ のグラフの下側にある傾き $p$ の直線を考えると、$x=a$ のところで $f$ と一致するような直線が $y$ 切片最大になるためです。上で述べた性質だけだと、$y$ 軸方向の平行移動分の自由度が残りますが、これと自明な性質 $f^{\star}(0) = -\min_f$ などを合わせれば $f^{\star}$ が確定できます。
slope trick の凸共役
slope trick (1) 解説編 では、次の性質を満たす区分線形凸関数に対して、いくつかの操作を高速化しました:
- 傾きが、すべて絶対値の小さな整数である
本記事では、凸共役が slope trick で扱った関数になるような区分線形凸関数を考えます。つまり、次を満たす区分線形凸関数です。
- 傾きの変化点の座標が、すべて絶対値の小さな整数である
以下、$f$ がこの性質を満たすとします。$f$ に対する操作を凸共役によって $f^{\star}$ に対する操作に取り換えることで、$f^{\star}$ に対する slope trick を用いて $f$ に対する操作を高速化することを slope trick の凸共役 と呼びましょう。
slope trick では、区分線形凸関数 $F$ を次のデータによって管理しました。
- $F$ の最小値
- 最小値の左側での傾きの変化点全体 $L$(priority queue で持つ)
- 最小値の右側での傾きの変化点全体 $R$(priority queue で持つ)
したがって、slope trick の凸共役では、区分線形凸関数 $f$ を次のデータによって管理します。
- $f(0)$
- 各非負整数 $n$ に対する $[n,n+1]$ での傾きを並べた列 $(R_0, R_1, \ldots)$ (priority queue で持つ)
- 各非負整数 $n$ に対する $[-(n+1),-n]$ での傾きを並べた列 $(L_0, L_1, \ldots)$ (priority queue で持つ)
可能な操作
高速化できる操作を確認しましょう。以下、$N$ と書けばその時点で保持している priority queue の要素数です。
$f(0)$ の取得:$O(1)$ 時間
$f(0)$ を管理するので当たり前です。
定数関数の加算:$O(1)$ 時間
$f(0)$ に加えるだけです。
$\min_{x}\bigl(f(x){}-{}px\bigr)$ の取得、特に $\min_xf(x)$ の取得:$O(N\log N)$ 時間
これは $-f^{\star}(p)$ の計算と等価です。slope trick (1) 解説編 より
$$f^{\star}(p) = {\min}_{f^{\star}} + \sum_{l\in L}(l-p)_+ + \sum_{r\in R}(p-r)_+$$
が成り立ち、$\min_{f^{\star}} = -f(0)$ なのでよいです。slope trick は最小値の取得が容易で $f(0)$ の計算は難しいですが、slope trick 凸共役では $f(0)$ の取得が容易で最小値の取得は難しいです。
平行移動 $f(x) \gets f(x\pm 1)$:$O(\log N)$ 時間
$f$ のグラフを直接考えてもよいですが、練習も兼ねて極小畳み込みと凸共役を利用します。
$$g(x) = \begin{cases}0 & (x=1) \\ \infty & (x\neq 1)\end{cases}$$
となる $g$ をとると、$f(x+1) = \bigl(f\mathop{\Box}g\bigr)(x)$ です。よって、凸共役にうつれば $g^{\star}$ を加算する操作ができればよいです。
$g^{\star}(p) = p$ が成り立ちます。したがって、$f^{\star}(p) \gets f^{\star}(p) + p$ という操作を考えればよいことになります。
- $L$ の最大値を $L_0$ とする。これは操作の前後でともに $f^{\star}$ が最小な点である。
- $f^{\star}$ の最小値に、$L_0$ を加算する。したがって、$f(0)$ に $L_0$ を加算する。
- $L_0$ を $L$ から pop して、$R$ にうつす
とすればよいです。$f(x)\gets f(x-1)$ の場合には、凸共役に $-p$ を加えることを考えれば同様にできます。
座標変化の小さな平行移動については、これらを繰りかえせばよいです。座標の大きい平行移動は(slope trick では簡単だったのに対して)slope trick の凸共役では扱いにくいです。
$cx$, $c(x-0)_+$, $c(0-x)_+$ の加算:$O(1)$ 時間
これは凸共役をとらず $f$ のまま考えれば自明です。$R$ 全体に $c$ を加算したり、$L$ 全体に $-c$ を加算したりすればよいです。
平行移動と組み合わせれば、絶対値の小さい整数 $a$ に対して $c(x-a)_+$ などの加算ができます。また、これらを両方行えば、$c|x|$ の形の関数の加算が行えます。
slope trick では、大きな $c$ に対する $c|x|$ の加算などは扱えませんでしたが、slope trick の凸共役では $c$ が大きくても簡単です。
スライド最小値関数 $f(x) \gets \min_{y\in [x-b,x-a]}f(y)$:$O((|a|+|b|)\log N)$ 時間
極小畳み込みを用いて、計算方法を導出しましょう。
$$g(x) = \begin{cases}0 & (x\in [a,b])\\ \infty & (x\notin [a,b])\end{cases}$$
とすると、$f$ を $f\mathop{\Box} g$ にうつす操作が求めるものです。したがって、$f^{\star}$ に $g^{\star}$ を加える操作を考えます。
$g^{\star}$ は $x=0$ の前後で傾きが $a$ から $b$ に変化するような折れ線です。これは $ax + (b-a)(x-0)_+$ などと書けるので、$f^{\star}$ に対する slope trick の基本操作 $O(|a|+|b|)$ 回でこれが行えます。

