概要
解法
$d_i, g_i$ のことを、この解説では $a_i, b_i$ と書いていきます(輸送コスト $a_i$・生産コスト $b_i$)。
基本方針
左から順に、生産個数を決めていきます。
地点 $i$ から $i+1$ に向かって $x$ 個輸送するとして、
- 地点 $i$ の生産コストまで計算したときの最適コスト:$f_{i}(x)$
- その区間の輸送コストまで計算したときの最適コスト:$g_{i}(x)$
として、$f_i, g_i$ を定めます。
- $g_0(x) = \begin{cases}0 & (x = 0)\\\infty & (x\neq 0)\end{cases}$
- $f_{i}(x) = \min(g_{i-1}(x+1), g_{i-1}(x) + b_i, g_{i-1}(x-1) + 2b_i)$
- $g_i(x) = f_i(x) + a_i|x|$
により計算できます。答は $f_N(0)$ です。関数 $f_i, g_i\colon \Z\longrightarrow \R$ をうまく管理することで、この関数操作を高速に行うことが課題となります。
データの持ち方
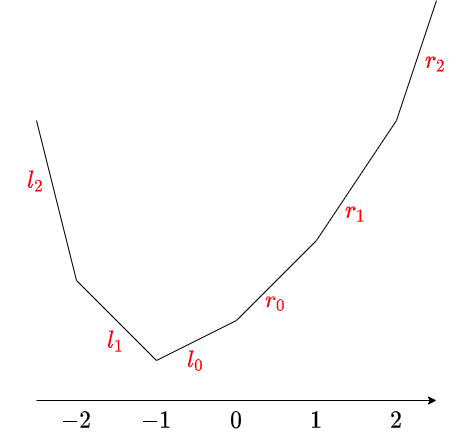
実は、上記の計算過程で現れる $f_i, g_i$ は、常に凸関数であることが分かります。なお、関数の定義域は $\Z$ ですが、定義域を上のように区分線形に $\R$ に拡張して扱っても答が変わらないことが確かめられます。
関数が常に下に凸になることを確かめながら、計算方法を整理しましょう。
データの持ち方としては、傾きの列 $(l_i), (r_i)$ を持つことにします。このような関数に対する次の $2$ つの操作を行う必要があります。
- $a|x|$ の加算
- $g$ が与えられたとき、それを $f(x) = \min(g(x+1), g(x) + b, g(x-1) + 2b)$ で定まる $f$ に取り換える
$a|x|$ の加算については、$x\leq 0$ 部分の傾きに $-a$、$x\geq 0$ 部分の傾きに $+a$ をすればよいです。関数の凸性を保つことも明らかです。よって後者の操作が問題となります。
極小畳み込みと Fenchel 変換
$f(x) = \min(g(x+1), g(x) + b, g(x-1) + 2b)$ という $g, f$ の関係について調べます。
関数 $h\colon \R\longrightarrow \R\cup \{\infty\}$ を、$$h(x) = \begin{cases}b(x+1) & (-1\leq x \leq 1)\\\infty & (|x| > 1)\end{cases}$$ により定めます。このとき、$f(x) = \inf_{y\in \R} (g(x-y) + h(y))$ と書くことができます。この右辺は、$g, h$ の極小畳み込み(infimal convolution)と呼ばれるものに相当します。以下、これを $g\Box h$ と書くことにします。$g, h$ が凸ならば、$g\Box h$ も凸であることが簡単に確かめられます。
また、$f\colon \R\longrightarrow \R\cup\{\infty\}$ (ただし恒等的には $\infty$ でない)に対して、$f^{\star}(p) := \sup(px-f(x))$ により定まる関数を $f$ の凸共役、凸共役をとる操作をFenchel変換などと言います。この問題で現れる関数の場合、Fenchel変換は次のような関係となります。
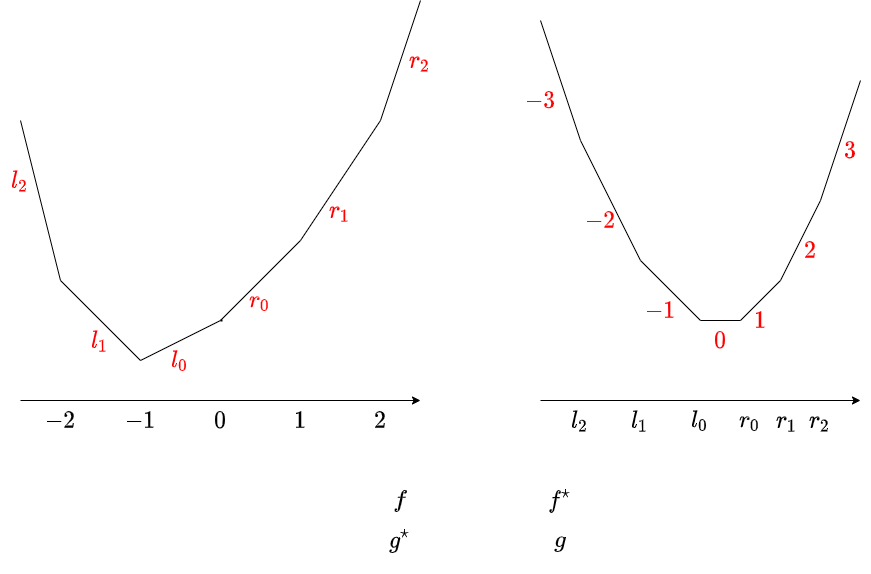
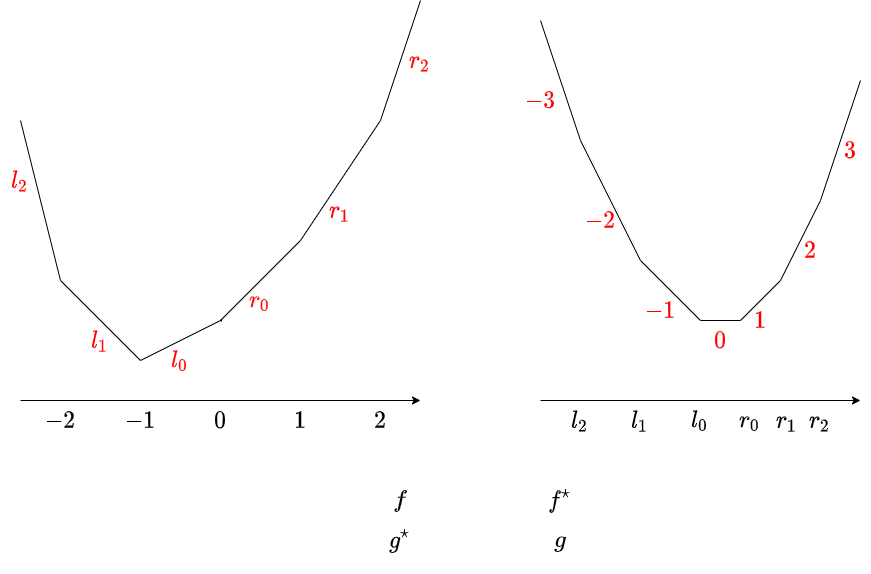
適切な条件を満たす凸関数 $f$ に対して、$f^{\star \star} = f$ が成り立ち、特に上の図の $2$ つの区分線形凸関数は、お互いに Fenchel 変換の関係になります。
極小畳み込みとFenchel 変換について、次が成り立ちます:
$$(g\Box h)^{\star}(p) = g^{\star}(p) + h^{\star}(p)$$
【証明】次の式変形により示される。
$$\begin{align*}(g\Box h)^{\star}(p) &= \sup_{x\in \R}(px-g\Box h(x))\\&=\sup_x(px-\inf_{y} (g(x-y)+h(y)))\\&=\sup_{x,y}(px-g(x-y)-h(y))\\&=\sup_{x,y}((p(x-y)-g(x-y))+(py-h(y)))\\&=g^{\star}(p) + h^{\star}(p)\end{align*}$$
$f(x) = \min(g(x+1), g(x) + b, g(x-1) + 2b)$ の計算
$f = g\Box h$ より $f^{\star} = g^{\star} + h^{\star}$ が成り立ちます。よって、凸共役にうつって $h^{\star}$ を加算する操作を考えます。
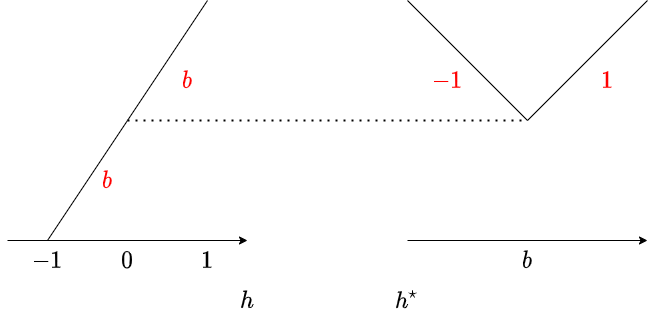
$h^{\star}(x) = |x-b| + b$ なので、$f^{\star} = g^{\star} + |x-b|+b$ が成り立ちます。したがって、この操作は slope trick により効率的に計算できます。
コメント
結局のところ、傾きの変化点が整数であるような区分線形凸関数に対して、傾きの列を管理することで、次が行えることが分かります。
- $a|x|$ の加算。より細分化すれば、$a \max(x,0)$ や $a\max(-x,0)$ の加算
- 同種の関数との極小畳み込み
- slope trick とは、傾きに注目することで区分線形凸関数を上手く取り扱う方法
- 記事「slope trick (1) 解説編」で扱ったものは、「傾きに整数性がある場合の slope trick」
- この記事で扱ったものは、「傾きの変化点に整数性がある slope trick」
- それらは Fenchel 変換の関係
という理解になるのかなと思います。(「slope trick」という言葉自体、まだ十分に普及しておらず、その指示範囲も明確な合意はないと思いますが、いかがでしょうか。)

