概要
本記事では、次の離散対数問題の変種を扱います。
$X$ をモノイド、$S$ を集合とし、$X$ が $S$ に左作用しているとする。
$x\in X$ および $s, t \in S$ および、正整数 $N$ が与えられる。次を満たす非負整数 $n$ が存在するか判定し、あればそのうち最小のものを求めよ:$x^ns = t$ かつ $0\leq n < N$
モノイドの演算や作用,および $S$ の要素のハッシュが $O(1)$ 時間で計算できるときに、本問題を期待時間 $O(\sqrt{N})$ で解くことを目指します。任意の非負整数を対象として最小の $n$ を求めたい場合には、$N = |S|$ ととればよいです。
左作用とは写像 $X\times S\longrightarrow S; (x,s) \longmapsto xs$ であって、単位元が自明に作用し、$(x_1x_2)s = x_1(x_2s)$ が成り立つものです。なおこの記事の範囲ではモノイドの要素は固定した $x$ に対する $x^n$ という形のものしか出てこないため、演算の左右の区別は不要です。(なので、「左作用」としましたが「右作用」の場合も同じです。)
上の問題は、特殊ケースに次のいわゆる「離散対数問題」(wikipedia)を含んでいます。
$X$ を群とし、$x, y \in X$ とする。$x^n = y$ を満たす非負整数 $n$ が存在するかを判定し、存在するならば求めよ。
具体的には、$S = X$ として、群演算そのものを作用と見なし、$s$ を単位元とすればよいです。
離散対数問題の解説記事でもこの特殊ケースを扱っているものが多いように思いますが、その定式化を直接は適用できない競技プログラミングの問題をしばしば目にするため、本記事の定式化・手法を考えました。例えば、次の問題が本記事の直接的な適用範囲となります:
$m, a, b, s, t$ が与えられる。$f(x) = (ax+b)\bmod m$ という関数を考える。
$f^n(s) = t$ (左辺は $n$ 個の合成)を満たす $n$ が存在するかを判定し、存在するならばそのうち最小のものを求めよ。
$X$ を $\mathbb{Z}/m\mathbb{Z}$ 上のアフィン関数全体(演算は合成)。$S = \mathbb{Z}/m\mathbb{Z}$ とした場合となります。
この問題は、$X=S$ を仮定した定式化では直接は扱いにくいと思います。また、$\gcd(a,m) = 1$ を仮定しない場合にも、合同式に関する性質などを使わずに直接適用できる解法を目指します。
本記事のアルゴリズムは、競技プログラミングではよく知られている baby step giant step アルゴリズムの変種ですが、モノイド(群とは限らない)による定式化では $x\in X$ の逆元の存在を仮定できないことに配慮する必要があります。
参考文献
- 問題
- 底と mod が互いに素でない離散対数問題 https://habara-k.hatenadiary.jp/entry/2021/10/14/230035
アルゴリズム
$m$ を適当にとり、集合 $T\subset S$ を $T = \{x^it\mid 1\leq i \leq m\}$ により定めます。$T$ の要素をハッシュマップで管理します。
$x^ns=t$ ならば任意の $i$ に対して $x^{n+i}s = x^i t$ なので、$k = \lceil (n+1) / m\rceil$ に対して $x^{km}s \in T$ となることに注意します。
まず、$x^{km}s \in T$ となる最小の $k$ を求めます。これは、$s$ に $x^m$ を作用させていくことで計算します。$k$ の最小性より、$n < (k-1)m$ ならば $x^ns\neq t$ です。$(k-1)m\leq n < km$ の範囲は全探索することで、$n < km$ となる解が存在するならばそのうち最小の解が得られます。
$x^ns = t$ となる $n$ は存在するものの、上の方法で解が得られないのは、例えば次の図のような状況です。$S$ を頂点集合とし $s$ から $xs$ に有向辺を張った functional graph を考えます。
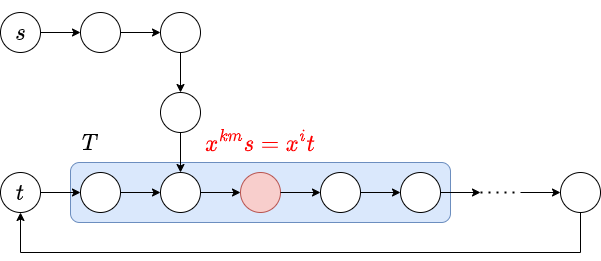
$x^{km}s = x^it$ から $t$ に到達可能であることが必要なので、$t$ はサイクル上の点です。したがって、$x^{km}s = x^it$ もサイクル上の点です。
この場合には、$x^{lm}s \in T$ となる $k<l$ のうちで最小のものを求めます。このような $l$ が存在しないならば、解なしです。このような $l$ をとったとき、$x^{km}s$ がサイクル上にあることから、$(l-1)m\leq n< lm$ かつ $x^ns = t$ となるような $n$ がこの範囲に必ず存在します。また $l$ の最小性より、$n < (l-1)m$ であるような解は存在しません。よって、$(l-1)m \leq n < lm$ の範囲を全探索すれば解が求まります。
なお、上の議論は $x^ns=t$ となる $n$ の存在を前提としていることに注意してください($t$ がサイクルに含まれない場合には、$(l-1)m\leq n < lm$ となる $n$ が存在しません)。
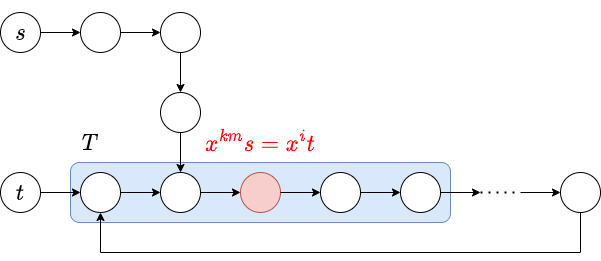
以上をまとめると、次のアルゴリズムが得られます。なお、探索範囲は制約 $n < N$ に合わせて適切に定めてください。
- $T = \{x^it\mid 1\leq i \leq m\}$ のハッシュ値を前計算しておく。
- $x^m$ を計算する。
- $k = 1, 2, 3, \ldots$ の順に、$x^{km}s \in T$ であるか否かを調べる。
- $x^{km}s\in T$ であるような $k$ に対して、$(k-1)m\leq n < km$ となる $n$ が $x^ns=t$ を満たすか否かを調べる。そのような $n$ が見つかれば、それが求めるものである。また、この全探索に 2 回失敗したら、解なしである。
$n$ の全探索が 2 回以下しか行われないため、上のアルゴリズムは期待時間計算量 $O\Bigl(m + \frac{N}{m}\Bigr)$ を達成します。例えば $m = \lfloor\sqrt{N}\rfloor$ ととることで、期待時間 $O(\sqrt{N})$ となります。
なお適切に実装すれば、アルゴリズムに現れる計算の回数はより詳細には次のようになります。
- モノイドの元の積の計算:$O(\log N)$ 回
- モノイドの元を集合に作用させる計算:$O(\sqrt{N})$ 回
モノイドの元の積は、$m$ 乗計算で一度用いられるのみです。
モノイドの元の積と作用で計算量の違いがある場合には、このことを意識した実装が計算量改善になりうるかもしれません(例えば、$X$ が $n\times n$ 行列全体、$S$ が $n$ 要素の列ベクトル全体である場合など)。

