概要
「Python で競技プログラミングをやる」の文脈で、高速フーリエ変換を使うための基礎知識を整理します。
高速フーリエ変換自体は競技プログラミング以外の文脈でも重要なアルゴリズムですが、そうした需要に応えることは、本記事では想定していません。
高速フーリエ変換の詳しいアルゴリズムにはこの記事では触れません(既存の解説が多数ありますし)。代わりにフーリエ変換についての基礎知識について、少し整理しました。ここは、使用言語に関係しない部分です。
最低限、Python での実装だけ見たい人は大部分を飛ばしてよいと思います。
フーリエ変換の性質
フーリエ変換の定義
詳しくは、本記事では扱いません。
$K$ を $1$ の $n$ 乗根を $n$ 個持つ体とします(競プロの文脈だと、$K=\C$ および $K=\F_p$ が重要です)。
$K$ に値を持つ数列 $A = (a_0,a_1,\ldots,a_{n-1})$ に対して、そのフーリエ変換 $\mathcal{F}_n(A) = (\hat{a}_0,\ldots,\hat{a}_{n-1})$ が定義されます。逆変換 $\mathcal{F}_n^{-1}$ というものもあります。また、これらの写像 $\mathcal{F}_n, \mathcal{F}_n^{-1}$ は $n$ に依存します。
※ 一般化としては…
- 有限アーベル群 $G$ とその双対加群 $\hat{G}$ に対して、$\mathcal{F}_G\colon K[G]\longrightarrow K[\hat{G}]$ が定義される
- 本記事で説明されるのは、$G = \Z/n\Z$ の場合
- 競プロだと、$G=(\Z/2\Z)^n$ の場合も有名(アダマール変換)
- アーベル群でない場合を含む一般化として、既約表現による群環の分解がある。興味のある方は「有限群の表現論」というキーワードに沿って学んでみてください。
畳み込みとの関係
数列 $A = (a_0,\ldots,a_{n-1})$ および $B = (b_0,\ldots,b_{n-1})$ の畳み込み $C = (c_0,\ldots, c_{n-1})$ を、$c_k = \sum_{i+j\equiv k\pmod{n}} a_ib_j$ により定めます(群 $\Z/n\Z$ での畳み込みということになります。周期 $n$ の巡回畳み込みという用語も見たことがあります。)。このとき、次が成り立ちます。
【畳み込み定理】
$\mathcal{F}_n(C)$ は、$\mathcal{F}_n(A)$ と $\mathcal{F}_n(B)$ の各点積に一致する:$\hat{c}_i = \hat{a}_i\cdot \hat{b}_i$。したがって $C = \mathcal{F}_n^{-1}(\mathcal{F}_n(A)\cdot \mathcal{F}_n(B))$ により畳み込みが計算できる。
特に、長さ $n$ の数列をフーリエ変換・逆変換するときの計算量を $F(n)$ とすれば、畳み込みを計算量 $3F(n) + \Theta(n)$ で行うことができます(定義に基づく単純なアルゴリズムによる計算量は、$\Theta(n^2)$ 時間です)。
高速フーリエ変換
この記事ではアルゴリズムには触れませんが、是非学んでみてください。
【高速フーリエ変換】
$n = \prod p_i$ と自然数の積に分解されるとき、$\mathcal{F}_n$, $\mathcal{F}_n^{-1}$ は計算量 $\Theta(n\sum p_i)$ で計算できる。特に $n = 2^k$ とすると,計算量は $\Theta(n\cdot 2k) = \Theta(n\log n)$ である。
したがって、次が得られます。
【高速フーリエ変換による巡回畳み込み】
$n = \prod p_i$ のとき、数列 $A = (a_0,\ldots,a_{n-1})$ および $B = (b_0,\ldots,b_{n-1})$ の畳み込み $C = (c_0,\ldots,c_{n-1})$ は計算量 $\Theta(n\sum p_i)$ で計算できる。
フーリエ変換自体は任意の $n$ に対して定義・計算ができます。定義に基づく単純な方法だとその計算量は $\Theta(n^2)$ になってしまうのですが、小さな素因数に分かれる場合に計算量が大きく改善されていて、その場合を高速フーリエ変換と呼びます。
群の表現の見方からは、部分群の搭 $\Z/n\Z=G_0\supset G_1\supset G_2\supset \cdots \supset G_k=0$ と誘導表現を利用して、フーリエ変換を分解していることになります(アーベル群でない場合にも一般化可能です)。
通常の加法による畳み込み(多項式の積)
上述の畳み込みは、$\Z/n\Z$ での加法に関するもの $c_k = \sum_{i+j\equiv k\pmod{n}}a_ib_j$ でした。$\pmod{n}$ をとらずに計算したいとします。例えば多項式の積がこれに該当します。
$A=(a_0,a_1,\ldots)$ および $B = (b_0,b_1,\ldots)$ に対して、$C = (c_0,c_1,\ldots)$ を $c_k = \sum_{i+j=k}a_ib_j$ により定めます。さらに
- $i\geq n_A \implies a_i = 0$
- $i\geq n_B \implies b_i = 0$
を満たすとします。$n_C = n_A + n_B-1$ とすると、$i\geq n_C\implies c_i = 0$ が分かります。
そこで、$n \geq n_C$ をとって、$\Z/n\Z$ での畳み込み(周期 $n$ での巡回畳み込み)を行います。$i,j,k< n_C$ に対して$i+j\equiv k\pmod{n}\iff i+j=k$ となるところがポイントで、$\Z/n\Z$ での畳み込みの計算結果を $D = (d_0,d_1,\ldots,d_{n-1})$ とすれば、任意の $i < n_C$ に対して$c_i = d_i$ となることが分かります。
したがって、巡回畳み込みを利用して、通常の加法による畳み込みも計算できました。「$\Z$ を $\Z/n\Z$ に埋め込む!?」という面白いアイデアです。
特に、$n$ として、$n_A+n_B-1$ 以上の最小の $2$ べきを選ぶことで、次が得られます。
【高速フーリエ変換による畳み込み】
数列 $A = (a_0,a_1,\ldots)$ および $B = (b_0,b_1,\ldots)$ があり、$i\geq n_A \implies a_i = 0$, $i\geq n_B\implies b_i = 0$ が成り立つとする。これらの畳み込み $C = (c_0,c_1,\ldots)$ ($c_k=\sum_{i+j=k}a_ib_j$)は、計算量 $\Theta((n_A+n_B)\log(n_A+n_B))$ で計算できる。
全く同じことですが、多項式の形でも述べておきます。
【高速フーリエ変換による畳み込み】
多項式 $A, B$ の積は、計算量 $\Theta((\deg(A)+\deg(B))\log(\deg(A)+\deg(B)))$ で計算できる。
余談ですが、競プロ文脈だと、以上の手順による「畳み込みの計算」全体のことを「高速フーリエ変換」と呼んでしまっている文献も時々見かけるように思います。あくまで高速フーリエ変換は、畳み込みで用いられるサブアルゴリズムという理解が正しいと思います。
numpy.fft の利用
基本の実装
基本的なことは、公式のドキュメントをちゃんと読むのが良いと思いますが。
一応、簡単な実装をしてみましょう。
FFT では、変換前の数列に加えて、どの周期(どの $\Z/n\Z$)で変換するかを指定します。何も指定しなければ、入力長と同一の周期でフーリエ変換されます。また、「高速」フーリエ変換とはいえ、この長さがいい加減だと速くなかったりします。ここでは $2$ べきの長さで実装しました。
細かいですが、入力に実数しかない場合には numpy.fft.fft に比べて、numpy.fft.rfft の方がパフォーマンスがすこし良いです。
numpy.convolve との比較
numpy には、畳み込み用の関数 numpy.convolve もあります。こちらは計算量 $\Theta(N^2)$ になっています。
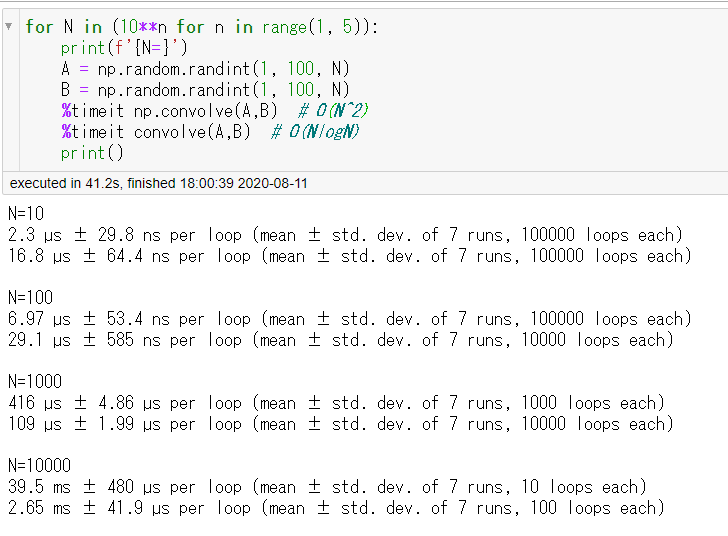
長さ 1000 くらいから、FFT に基づく方法の方が速くなっているようです。
$n$ の選択

fft に用いる長さは、必ずしも $2$ べきである必要はありません。次の $2$ べきが遠い場合、小さな素数に分解できる適当な長さを選ぶ方がパフォーマンスが良い場合もあります。
mod p での計算
$f,g$ を $n$ 次多項式とし、積 $h = fg$ を計算したいとします。特に、これを $\pmod{p}$ で計算せよというのが競プロ文脈でよくある状況です。$p$ としては、$10^9+7$ や $998244353$ が一般的です。
この際、計算誤差が問題となります。$|f_i| < p$, $|g_j| < p$ としたとき、$|h_i| < np^2$ ですが、$n=10^5$ かつ $p=10^9+7$ だと $np^2$ は $10^{23}$ 程度にまでなるため、64bit浮動小数点数で正しく計算できる範囲を大きく超えます。
そこで、上下 15 bit ずつに分けるというテクニックを使うことができます。

$f = 2^{15}f_1 + f_2$, $g = 2^{15}g_1 + g_2$ として、$fg = 2^{30}f_1g_1 + 2^{15}(f_1g_2+f_2g_1) + f_2g_2$ と式変形をします。係数が小さな多項式の積は、64bit浮動小数点数の有効数字で正しく計算できるので、それらを合わせて $fg$ の計算に戻しています。畳み込み(多項式の積)の他、行列の積でのお手軽オーバーフロー回避としても利用できるテクニックです。
$f_1g_2+f_2g_1$ は、ふつうに考えれば畳み込み $2$ 回が必要ですが、上手い方法で $1$ 回節約しています。これは カラツバ法 と同じことをやっています。
これで、競プロで FFT を要求されるほとんどの場合に対応できると思います。
なお、FFT+$\bmod p$ の計算では $3$ 回の畳み込みを必要としていますが、$1$ の $n$ 乗根をとれる $p$ については FFT を体 $\F_p$ に適用した場合(NTTともよばれる)の方が高速です。これを想定解とする問題のほとんどは $p=998244353$ での出題かと思います。これは numpy.fft にはありませんので、$3$ 倍遅いことを受け入れるか、自分で NTT の実装を勉強するということになるかと思います。

