参考文献
- Elegia さん:https://codeforces.com/blog/entry/92183
- 転置原理により本記事で扱う問題の解法が導出できることについて述べている.
- ryuhe1 さん:https://qiita.com/ryuhe1/items/c18ddbb834eed724a42b
- 転置原理について詳細な記述がある.
- noshi91 さん:https://noshi91.hatenablog.com/entry/2023/04/05/023553
- Library Checker:https://judge.yosupo.jp/problem/power_projection_of_set_power_series
転置写像と転置原理
転置写像の簡単な説明は「行列で書いたときに転置行列になるやつ」なのですが,私は写像を行列で書くのが苦手なので,線形写像の言葉で一応書いておきます.
転置写像(抽象的な定義)
$K$ を環とし,$M, N$ を自由加群,$F\colon M\longrightarrow N$ を $K$ 線形写像とする.このとき $K$ 線形写像 $F^{T}\colon \mathrm{Hom}_K(N, K) \longrightarrow \mathrm{Hom}_K(M, K)$ が $\phi\mapsto \phi\circ F$ により定まる.これを $F$ の転置写像という.
というのが抽象的な定義です.
転置写像(成分による定義)
$K$ を環とし,$F\colon K^n\longrightarrow K^m$ を $K$ 線形写像とする.$f$ の転置写像 $F^{T}\colon K^m\longrightarrow K^n$ とは,次によって一意に定義される線形写像である.
- $(x_1, \ldots, x_m)\in K^m$ とする.$f_1, \ldots, f_n \in K^n$ に対して $(g_1, \ldots, g_m) = F(f_1, \ldots, f_n)$ としたとき,$\sum_jx_jg_j = \sum_iy_if_i$ が任意の $(f_i)$ に対して成り立つような $(y_1, \ldots, y_n)$ が一意に存在する.これを $F^{T}(x_1, \ldots, x_m)$ と定める.
よって,「$F^{T}(x_1, \ldots, x_m)$ を計算せよ」という問題は「$\sum_j x_jg_j$ という式を $\sum_i y_if_i$ と表せ」と考えることができます.「$\sum_j x_jg_j$ という式における各 $f_i$ の寄与を求めよ」と考えてもよいでしょう.
なお,$F$ と $F^T$ では始域と終域が入れ変わっていますが,逆写像というのとは全然違うので注意してください.
転置原理
転置原理とは大雑把にいえば,次の $2$ つの問題が同程度の計算量のアルゴリズムを持つというものです:
- $f = (f_1, \ldots, f_n)$ を入力として $F(f) = (g_1, \ldots, g_m)$ を出力する問題
- $x=(x_1, \ldots, x_m)$ を入力として $F^{T}(x) = (y_1, \ldots, y_n)$ を出力する問題
$F$ のアルゴリズムから $F^{T}$ を導出することは, $F$ のアルゴリズムの算術演算を全て列挙していけば原理的にはできるはずですが,アルゴリズムが複雑だとそのような方法での機械的なアルゴリズム導出は大変です.実際には,算術演算単位ではなくもう少し大きなステップのアルゴリズムに分解して,各ステップの転置問題を(転置原理を用いずに)解くことで導出することが多いと思います.本記事でもそのような手順で,合成の転置写像の計算方法を導出します.
多項式と集合べき級数の合成の転置(定式化)
上の問題が「多項式 $f$ と集合べき級数 $a$ の合成」を転置したものと見なせる理由について説明します.
「$f$, $a$ を入力として $f(a)$ を出力する」という写像は線形写像ではありません.多項式との合成の転置といった場合には,転置前の問題としては次の問題を考えています.
- 集合べき級数 $a$ を固定する.多項式 $f$ が入力されるので,$f(a)$ を出力せよ.
写像 $F\colon f\longmapsto f(a)$ は線形写像です.(例えば多項式 $f_1, f_2$ に対して $(f_1+f_2)(a)=f_1(a)+f_2(a)$ が成り立ちます.)
よってこの問題の転置を考えることができます.(一方,$f$ を固定して $a\longmapsto f(a)$ を考えてもこれは線形写像ではなく,転置写像を考えることはできません.)
転置問題は次のようになります:
- 集合べき級数 $a$ を固定する.列 $(x_0, \ldots, x_{2^{n}-1})$ が与えられるので,任意の多項式 $f(x) = \sum_{k}f_kx^k$ に対して $\sum_s x_s [x^s]f(a) = \sum_k y_kf_k$ が成り立つような $(y_k)$ を出力せよ.
$[x^s]f(a)$ における $f_k$ の寄与は当然 $[x^s]a^k$ なので,次のようになります.
- 集合べき級数 $a$ を固定する.列 $(x_0, \ldots, x_{2^{n}-1})$ が与えられるので $y_k = \sum_{s}x_s [x^s]a^k$ により定まる列 $(y_k)$ を計算せよ.
これは集合べき級数のべき乗(power)の係数列の線形結合を評価する問題で,Power Projection という問題の特殊ケースと考えることができます.
EGF による Power Projection
$f$ が EGF である場合に Power Projection を計算します.改めて次のように問題を定式化しておきます.
- 集合べき級数 $a$ と長さ $2^n$ の列 $x$ が与えられる.EGF $f = \sum_k f_k\frac{x^k}{k!}$ に対して $X = \sum_s x_s[x^s]f(a)$ という式を考える.$X$ における各 $f_k$ の寄与を求めよ.
転置原理によりこの問題は $\Theta(n^22^n)$ 時間で解けるはずです.その具体的なアルゴリズムを導出しましょう.転置写像は,もとの写像の計算手順を逆向きに辿ることで計算できます.おおよそ次のような計算手順になります.
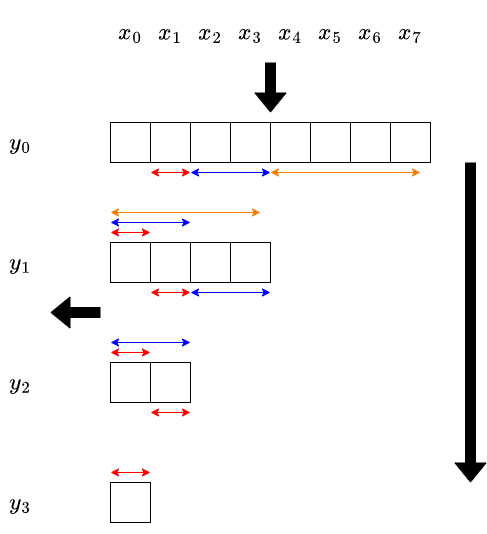
より具体的には,上図の各マスに対して,そのマスの $X$ への寄与を求めていきます.一番上の行の各マスの寄与が与えられていて,一番左の列のマスの寄与を求めればよいということになります.
ある行から次の行を計算する部分を取り出します.
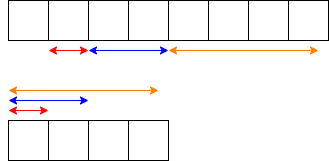
上の行の各マスがある値 $X$ にどのような係数で寄与しているかが与えられたとき,下の行の各マスの $X$ への寄与係数を求めればよいです.これは,赤い矢印・青い矢印・橙の矢印による遷移の寄与をそれぞれ足し合わせればよいです.
これらそれぞれの遷移は,入力として与えられている列 $a$ のスライスとの subset convolution でした.したがって,次ができればよいです:
- 集合べき級数 $c$ と数列 $x$ が与えられる.「$c$ との subset convolution を求める」という写像($a\longmapsto a\star c$)の転置写像による $x$ の像を計算せよ.
つまり,$b = a\star c$ としたときに,$\sum_{s}x_sb_s = \sum_{s}y_sa_s$ が成り立つような列 $(y_s)$ を求めればよいです.subset convolution の定義を使って式変形すると,左辺は$\sum_{t_1\cap t_2 = \emptyset}x_{t_1\amalg t_2}a_{t_1}c_{t_2}$ と書けるので,$a_s$ の係数を取り出すことで $y_s = \sum_{s\cap t = \emptyset}x_{s\amalg t}c_t$ が求めるものであることが分かります.
適切に補集合に取り換えると,$\mathrm{reverse}(y)$ が $\mathrm{reverse}(x)$ と $c$ の subset convolution であることが分かります.
よって,$c$ との subset convolution の転置写像は,reverse・$c$ との subset convolution・reverse をこの順に計算すれば求まることが分かりました.
以上をまとめると,例えば次のように実装できます.
多項式との合成の転置
多項式 $f$ との集合べき級数 $a$ の合成は,$c=[x^0]a$ として次の手順で計算できました.
- $g(x) = f(x+c)$ を $n$ 次まで計算する.
- $g$ を EGF になおす(係数に $k!$ をかける)
- $a-c$ との合成を計算する.
EGF と $a-c$ の合成については既に転置写像の計算方法を解説しました.係数ごとの $k!$ 倍については対応は容易です.残る課題は次の通りです:
- 多項式 $f$ から $g(x) = f(x+c) \bmod x^n$ を計算する写像の転置を計算せよ.
$f$ から $g$ を得る写像は $g_j = \sum_{i}\binom{i}{j}f_ic^{i-j}$ と書けます.よって $\sum_{j} x_jg_j = \sum_{i,j}\binom{i}{j}f_ic^{i-j}x_j$ なので,各 $f_i$ の寄与を取り出すことで転置写像は $y_i = \sum_{j}\binom{i}{j}c^{i-j}x_j$ により計算できることが分かります($i$ ごとに $O(n)$ 時間で計算できます).

