A. Double Perspective
$f,g$ それぞれの最適値を達成できます.何かに含まれる区間を除く操作を可能な限り繰り返します.この操作で $f$ は変化しません.
のこった区間を $(L_i,R_i)$ とすると,同じ点を左端とする区間や同じ点を右端とする区間は存在しないので $g$ は $0$ であることが分かります.
B. Stay or Mirror
$p_i<p_j$ のとき,$p_i$ から見て $p_j$ が転倒しているかを数えることにします.
すると,$p_j$ に対する操作の選択が転倒しているかに無関係になっています.なので,$i$ ごとに独立に最適化できます.
C3. Interactive RBS (Hard Version)
インデックスは自由順で何度でも選べるという重要制約を見落とさないように注意します.
カッコを L, R と書くことにします.まず,$10$ 回程度でひとつ R を見つけます.S[0] が L であると仮定して,S[0]S[i_1]…S[i_k] が正である状態を維持する二分探索をすればよいです.失敗したら S[0] は R です.
ここから $1$ クエリあたり $13$ 個ずつ決めていきました($12$ 個ずつで AC 可能なはず).
未知の文字を A, B, C, D, … として次のような質問をします:
AR R BRBR R CRCRCR R DRDRDRDRDR R …
途中に R を挟むことによって,このクエリの結果は
(A==L ? f(1) : 0) + (B==L ? f(2) : 0) + …
のような形になります.よって,$f(1), f(2), …$ の subset sum が distinct になるような列を適当にとればよいです.貪欲に足せるものを足していくという方法などをとればよいです.私は手作業二分探索みたいな実装をして足していきました.
だいたい $\sqrt{2}$ 倍で増えていく等比数列の個数を使うと $f$ が $2$ 倍程度に増えていくので subset sum 条件は大丈夫で,$13$ 種でクエリ長 $1000$ 以下という条件も大丈夫です.
D. Permutation Blackhole
木を描いたのですが,あまり木を意識せずそのまま区間 DP していくということで?
雑に書くと,とても $1$ より小さな定数倍がつくタイプの $O(N^6)$ になり,手元ランダムケース $4$ 秒程度になりました.
あと何かひとつ計算量を落とせば良さそうで,$a_i\geq 0$ となる $a_i$ の総和が $N$ 以上なら答は $0$ であるという枝狩りをしました.$a_i$ の上限が $O(\log N)$ であるという方法もあるようです.
ロジックは簡単で,
- $L,R$ が黒い状態から $[L+1,R-1]$ 部分の操作を決めるときの
- その範囲の操作では最終的に $L,R$ が $x,y$ 回選ばれるような方法の総数
を $\dp[L][R][x][y]$ などとしてこれを計算していきます.初手 $M$ をループします.
$\dp[L][M]$ 部分と $\dp[M][R]$ 部分を,$M$ に対する操作回数が適切になるように注意してマージします.
E. Induced Subgraph Queries
Mo をやることを考えます.$(l,\ldots,r)\leftrightarrow (l,\ldots,r,r+1)$ のコストが $O(\deg(r+1))$ かかりそうなことだけが問題です.
でもやっぱり Mo が使えます.典型ではあると思います.
- $(l,\ldots,r)\leftrightarrow (l+1,\ldots,r)$ のコストを $a_l$
- $(l,\ldots,r)\leftrightarrow (l,\ldots,r,r+1)$ のコストを $b_r$
として,区間 $(l,\ldots,r)$ に対して座標 $(\sum_{i<l}a_i, \sum_{i<r}b_i)$ を考えると,点のマンハッタン距離がコストになっています.よって,$\sum a_i+\sum b_i$ が $O(N)$ の状況ならばいわゆる Mo の状況と同じ計算量が達成できます.
今回は,$a_i, b_i$ は $\deg(v)+1$ の類とすればよいです.「$+1$」をやらなかったら TLE になりました(反省).
あとは,値の上限が $O(n)$ であるような集合を管理して,
- 集合への追加削除:$O(n^{1.5})$ 回
- 集合の $k$ 番目の検索:$O(n)$ 回
を処理できればよいです.これも平方分割を使ってブロックごとの要素数を持てば,追加削除が $1$ 回あたり $O(1)$,検索が $1$ 回あたり $O(\sqrt{n})$ 時間になるので大丈夫です.
全体の計算量は $n+m+q$ を改めて $n$ として,$O(n^{1.5})$ です.
F2. Top-K Tracker (Hard Version)
F1, F2 それぞれ面白かったので,それぞれの解法を紹介します.
F1
はじめにクエリ 3 または 4 を使って,適当な $300$ 個のインデックスについて値の候補を得ておきます.$845=545+300$ と分解します.それぞれの値の集合は確定しています.
残りはクエリ 1 だけで処理します.$A$ を $545$ 個のインデックス,$B$ を $300$ 個のインデックスとして $Q = \{1,2,\ldots,29\}$ とします.
次が達成できればよいです.
- 各 $A, B$ の要素に $Q$ の部分集合を対応させる($1,2,\ldots,29$ 回のクエリのどれに含めるかを選ぶことに相当).
- 異なる $A$ の要素には異なる部分集合が対応している.
- 異なる $B$ の要素には異なる部分集合が対応している.
- 各 $t\in\{1,2,\ldots,29\}$ に対して,$t$ を含む部分集合に対応する要素は $60$ 個以下である.
大きさの小さい部分集合から順にクエリに詰め込んでいく(ただし各要素がバランスよく出現するようにする)とこれを達成できます.この部分は一般的には https://qoj.ac/contest/2036/problem/11112 のような構築があるのでした.
これでどのクエリも $60$ 要素以下になるようにできます.かなりきわどいです.
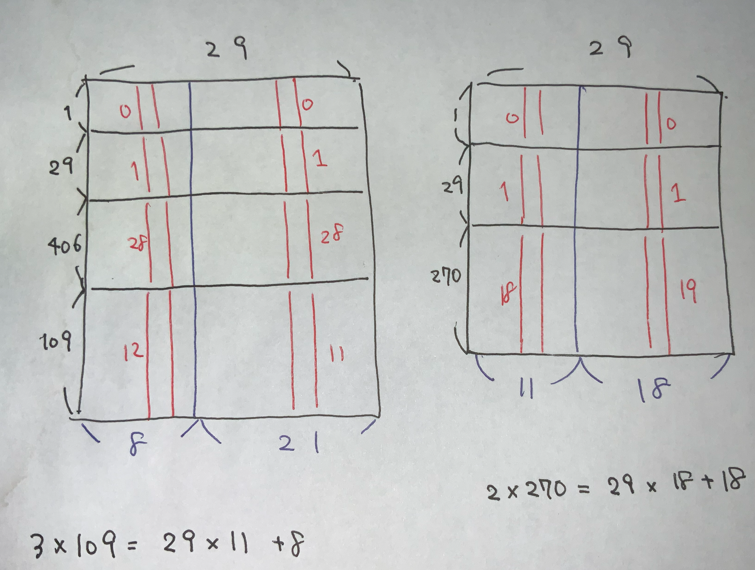
F2
$n=890$ とします.大きさ $0,1,2,3$ の部分集合に対応する $445$ 個の集合をとってきて,どの値も $30$ 回個の集合までにしか含まれないようにします.
これらの集合を $2$ 回ずつ使うと,次のようになります:
- インデックスのペア $(a_i,b_i)$, と値のペア $(c_i,d_i)$ であって,$P[a_i], P[b_i]\in \{c_i,d_i\}$ である.という形の情報が $n/2$ 組ある.
さらに,「インデックスのペア」については自分でコントロール可能であることに注意します.ここでは $a_i< n/2$ かつ $b_i\geq n/2$ であるようにペアを作っておきます.
最後に,各 $i$ について $c_i,d_i$ のうち一方を乱択して,選んだ $n/2$ 個の値をクエリ $4$ に投げます(ジャッジは adaptive ではないことに注意).
すると,クエリで得られるのは,「各 $a_i,b_i$ のうち一方を乱択して得られる $n/2=445$ 個の値のうちの top $300$」となります.
$300$ 個の値しか得られませんが,選んだインデックスのうちこの $300$ 個に含まれていないものは,ほぼ間違いなく $n/2$ 未満です.確率 $1/2$ の乱択を $445$ 回行って,片方の結果が $300$ 回以上出ている確率は非常に小さいからです(二項分布の標準偏差を $\sigma$ として,$7\sigma$ 近く離れている).
よってこれですべてのペアの情報を復元することができます.

