A. King of Thieves
すべての方法を全探索できます.
B. Om Nom and Dark Park
木dpで,各 subtree に対して,深さをそろえた場合の最小深さとコストを求めればよいです.
C. Om Nom and Candies
$H/W$ の大きい方を $H_1,W_1$ とします.2 種類目は $W_1$ 以下としてよいです(2 が $W_1$ 個あれば 1 を $W_2$ 個に変更してよい).一方 1 の個数は $C/W_1$ 以下なので,どちらかの個数で全探索すれば $O(\min(W_1,C/W_1))$ 時間で解けます.これは $O(\sqrt{C})$ 時間です.
D. Om Nom and Necklace
A+B の長さを固定して考えます.すると,A の長さとしてありうるものは,S と S の suffix の lcp から求まることは分かります.この lcp は Z algorithm で求まります.そうして valid な A の長さの範囲が分かればその区間の ANS を true にすればよいです.
E. Transmitting Levels
円環上の各点からどこまで進めるというのが与えらえていて,それに単調性があるとき,最小何回で一周できるかという問題です.
配列の長さを $2N$ にしておきます.各 $i\in [0,N)$ に対してはじめて $N$ 以上になるまでの部分のシミュレーションを考えます.このときの結果(回数と到達地点)は $i$ について降順に計算すると $O(N)$ 時間ですべて求まります.
F. Pudding Monsters
座標 x[i] に番号 y[i] の点があると思います.座標が隣接している 2 点を辺で結びます.頂点番号が区間で誘導部分グラフが連結になるような区間の数え上げです.これは有名問題で,木に一般化したものも含めて何度か出ています.
森の連結成分数が頂点数と辺数の差から分かることに注意します.$r$ をインクリメントしながら頂点 $l,\ldots,r$ の場合の頂点数と辺数の差 diff[l] を管理することを考えると,列への定数加算と最小値・最小値の個数の取得ができる遅延セグメント木で解けることが分かります.
G. Spiders Evil Plan
難しい.解説を見ても証明も半端だしオンラインクエリへの処理はほとんど書かれていなかったように思ってしまった.
前提としてタイブレイクの議論はさぼります.例えば直径といえば一意,深さ最大の部分木も一意と考えて議論しています.各辺の長さに独立な $\varepsilon$ を加えることを考えれば正当化できます.
根付き木の問題 (通る点の制約なし)
次の問題を考えます:根付き木が与えられる(辺重みあり).根から葉までのパスを $k$ 個選んで,通った辺重みの和を最大化せよ.
この問題は貪欲法により解けます.
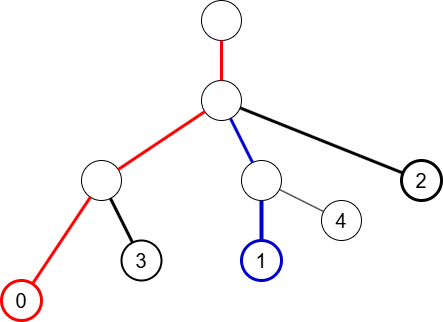
具体的には,「木の深さに関する HLD」を考えます(この概念に名前がついているのかはわからず,).つまり部分木サイズ最大ではなく高さ最大の部分木を heavy child として HLD を作ります(パスクエリの最悪計算量は通常の HLD よりも悪化します).
最適解はある頂点を含むなら必ずその “heavy child” も含むことが簡単に言えるので,最適解はこれらの “heavy path” に分割できます.この “heavy path” を長いものから貪欲にとったものは根を含む連結集合を与えることも簡単に言えるので,この問題は長いものから貪欲にとっていくというのが解になります.
根付き木の問題 (通る点の制約あり)
$v$ を通る必要があるとして解きます.まずは計算量を度外視して正当な解法を考えます.
この場合,heavy child の定義を次のように変更します:$v$ がある方向があるならそっちが heavy,そうでなければ最も深い部分木方向が heavy.
これでやはり,ある頂点を含む解はその heavy child を含むことが言えるので,同様に heavy path への分解をとって,貪欲に($v$ を含むものをまずとり,その後は長いものから)とっていけば解が得られます.
このことを踏まえて高速にクエリに答えられるようにしましょう.$v$ が制約なしの最適解に入っていたらそれが明らかに解です.そうでないとします.
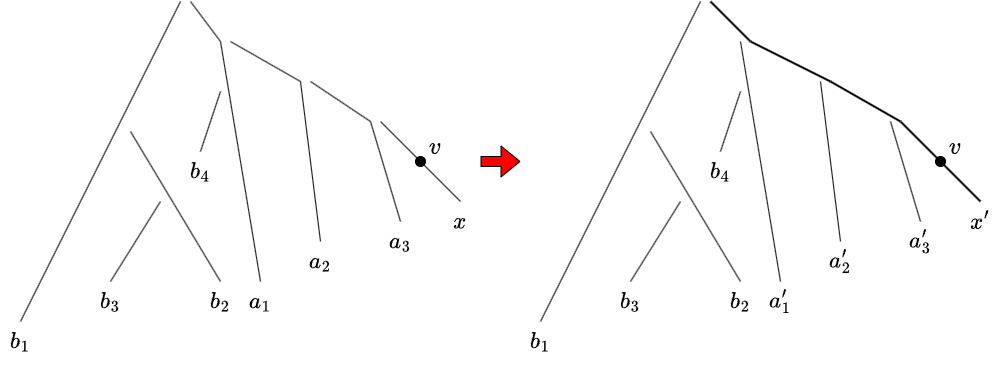
上図はパス分解の変化を表した図です.$v$ から根の部分にある頂点の heavy child の定義が変更されるため,その部分にあるパスが短くなります.それ以外のパスは影響を受けません.
影響を受けるパスを $a_i$,影響を受けないパスを $b_j$ とします.こうして変更したパスの集合に対して,$x’$ 以外の上位 $k-1$ 個のパスをとりたいということになります.
もとのパス分解での上位 $k$ 個を,$a_1,\ldots,a_p$,$b_1,\ldots,b_q$ とします(それぞれ長い方から).
このとき,次のことが言えます:変更後のパス分解での上位 $k-1$ 個は,$a_1′,\ldots,a_p’$, $b_1,\ldots,b_q$ の上位 $k-1$ 個(つまり最小値以外)である.
もともと上位 $k$ 個に入っていなかったものが変更後の上位 $k-1$ 個に入ってくることはないということです.$a_i’$ の形のものは明らかです.これは $a_i’ > a_{i+1}$ から分かります.
結局答を求めるには,もとのパス分解での上位 $k$ 個の和を求めておき,そこに含まれる $i,j$ に対して $a_i’, b_j$ の最小値を引けばよいです.最小の $a_i’$ の計算は木上の二分探索で出来て,それと元の $k$ 番目のパスの長さとの min をとれば引くべき値が分かります.
もとの問題
通る葉をひとつ固定して上の議論を考えれば,最適解は直径の端点のひとつを通ることが分かります.よって直径の端点を固定して $2$ 回解くことでもとの問題を解くことができます.
中心をとって $1$ 回で答を出すこともできると思いますが,選べる葉の個数の議論が少しややこしくなります.

