A. Recycling Center
$c$ 以下であるもののうち最大のものを使う貪欲法でよいです.
B. Deque Process
ある取り方をすると $2$ 手先で詰むする可能性があるというときに,逆の取り方をするようにすれば大丈夫です.ルールベースの戦略実装ではなく rollback dfs により実装しました.
C. Leftmost Below
先頭の項は最初に操作してしまうとしてよいです(そうでないとして操作順序を入れ替えることを考える).同様に考えると操作は先頭から順に行うとしてよいです.
結局 $a_1,\ldots,a_{i-1}$ が定められたときに $a_i$ を定められるかという問題だけを考えればよいことになります.
D. Sum of LDS
まずは $p$ 全体に対する LDS の計算を考えます.
$p_i<p_{i+1}<p_{i+2}$ となることはありません.$p_i>p_{i+1}$ となるときに $i,i+1$ の間で切ると,長さが $1$ または $2$ の増大列に分割されます.
この長さを $m$ とするとき,LDS 長は $m$ であることが証明できます.
- $m$ 個の増大列に分割できている.各増大列からは LDS へは高々ひとつしか採用できないため,LDS は $m$ 以下である.
- 長さ $m$ の減少列にとれる:各増大列の末尾をとってきたものが減少列であることが示せる.(長さ $1,1$ の成分,$1,2$ の成分,$2,1$ の成分,$2,2$ の成分が並ぶ場合それぞれで末尾が減少することが問題の条件からチェックできる).
これによって,subarray に対する答は,$p_i>p_{i+1}$ となる $i$ の個数から計算できることが分かります.
適当な累積和テーブルの前計算のもと,$[l,r]$ のスコアが $f(l)+g(r)$ の形で書けます.そのようなものの総和は,$f(l)$ の総和と $g(r)$ の総和に分割して計算することで $O(N)$ 時間で計算できます.
E2. Submedians (Hard Version)
まず E1 を解きます.「中央値が $x$ 以上にできる」という判定問題を考えます.
列 $b_i$ を $a_i\geq x$ ならば $b_i=1$,そうでないならば $b_i=-1$ として定めたとき,中央値に関する条件は,区間和が非負であると言い換えられます.そのような長さ $k$ 以上の区間が存在するかどうかは累積和テーブルなどを使って簡単に判定できます.二分探索と合わせて E1 が解けます.
E2 を解きます.重要な観察は次の通りです:
- 集合 $S$ の中央値区間と,一要素追加した集合 $S\cup \{a\}$ の中央値区間は交わる.したがって $[l,r]$ の中央値区間と,$[l,r+1]$ や $[l-1,r]$ の中央値区間は交わる.
これは本問の(あまり見かけない)中央値の定義のおかげです.
このとことから,
- 最小の中央値を実現する区間 $[L_1,R_1]$
- 最大の中央値を実現する区間 $[L_2,R_2]$
を求めて,$[L_1,R_1]$ から連続的に $[L_2,R_2]$ へ変化させることで,最小の中央値と最大の中央値の間の値をすべて実現することができます.変化順を適切に定めれば,常に長さは $k$ 以上にできます.
中央値は上側集合と下側集合の管理によって差分更新して計算してもよいですし,私は wavelet matrix を使用して計算しました.
F. Strict Triangle
dist の「$\neq$」が書いてありますが,「$\leq$」は明らかなので,「$<$」が成り立つようにすることが目標です.
解があったとして,$1$ から $n$ への最短路 $P$ をひとつ固定します.$P$ 上の辺を $x$ 短くするとき,左辺は $x$ 減って,右辺は $x$ 以下減少するため,解があればそのうちで $P$ 上の辺はすべて $w_i=l_i$ であるものがあります.その他の辺は長くしても解のままなので,$P$ の辺重みはすべて $l_i$ かつ他の辺重みはすべて $r_i$ であるような解が存在すると分かります.
$d_v$ を,すべての辺重みを $r_i$ とした場合の $k$ から $v$ までの重みとします.また $v,w\in P$ であるとき,$P$ 上での $v,w$ の距離を $P_{vw}$ とします.
必要条件 $P_{vw}<d_v+d_w$ は明らかです.
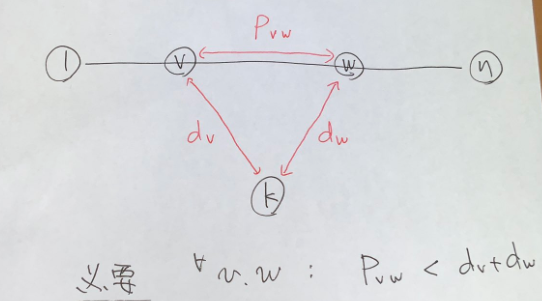
これは十分条件になって,次が成り立ちます:
- (最短路とは限らない)パス $P$ であって,任意の $v,w\in P$ について $P_{vw}<d_v+d_w$ が成り立つものが存在するとする.(このとき $P$ の長さが $\mathrm{dist}(1,k)+\mathrm{dist}(k,n)$ 未満であるとは限らないが))このような辺重みの定め方は条件を満たす.
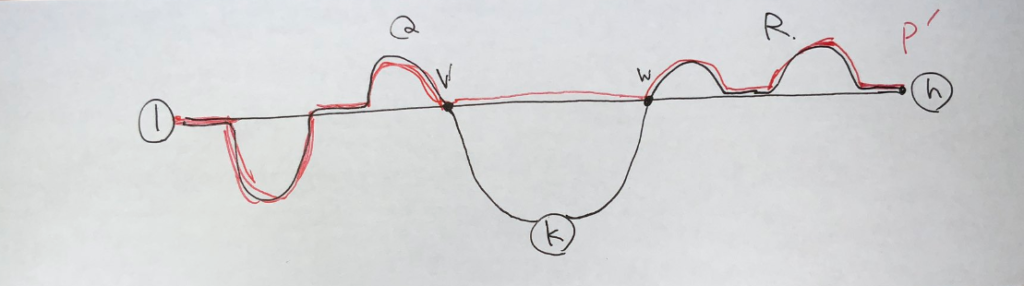
$k\to 1$ 最短路 $Q$ および $k\to n$ 最短路 $R$ をとって,これらがはじめて $P$ と交わる点を $v,w$ とします.$k$ から $v,w$ へのパス上の辺重みはすべて $r_i$ なので,この部分の距離は $d_v,d_w$ です.$d_v+d_w>P_{vw}$ であることから,$Q,R$ を結合して $v\to k\to w$ 部分を $P$ に置換したものを $P’$ とすれば,$P’$ の長さは $\mathrm{dist}(1,k)+\mathrm{dist}(k,n)$ 以下となります.
上で,次が示されています.
- 問題の解が存在するならば,パス $P$ であって,$P$ 上の辺重みをすべて $l_i$ としたときに任意の $v,w$ に対して $P_{vw}<d_v+d_w$ が成り立つ.
- パス $P$ であって,$P$ 上の辺重みをすべて $l_i$ としたときに任意の $v,w$ に対して $P_{vw}<d_v+d_w$ が成り立つものがあるとき,問題の解($P$ とは限らない)存在する.
$P$ 自体の特徴づけを得たわけではないという少し変わった証明ですが,言い換えに成功しました.
$\dp[i]$ を次のように定義します:$1$ から $i$ までのパス $P$ であって,任意の $v,w\in P$ について $P_{vw}<d_v+d_w$ を満たすものに対する $\min_v(P_{vi}-d_v)$ としてありうる最大値.
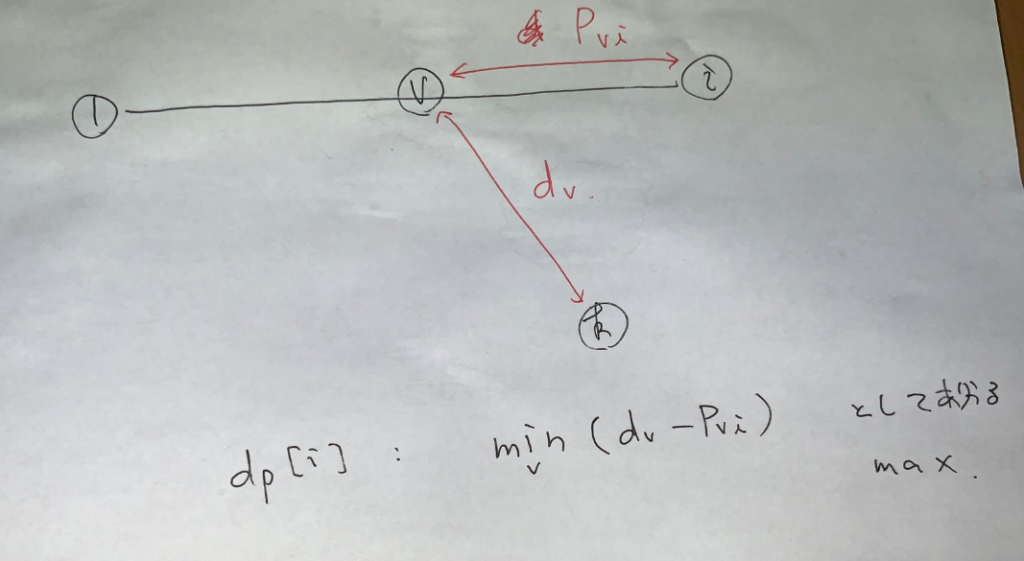
これが定義できればあとは簡単です.$i\to j$ へ辺重み $cost$ があるときの遷移を考えると,次のようになります.
- $\dp[j]\leftarrow \min(\dp[i]-cost,d_j)$.ただし遷移可能なのは $\min(\dp[i]-cost,d_j)+d_j>0$ となる場合のみ.
遷移によって $\dp[]$ が増えることはないので,dijkstra の要領で $\dp[]$ が大きい側から決定していくことができます.

