概要
公式解説と少し違う感じがしたので書いておきます。
最適な操作回数を理解する
数列を、ヒストグラムにより可視化します。$x$ 座標、$y$ 座標が定義できます。例えば、$A = [4,2,3,4,2,4]$ に対するヒストグラムは以下の形です。左右方向を$x$ 座標と見なします。
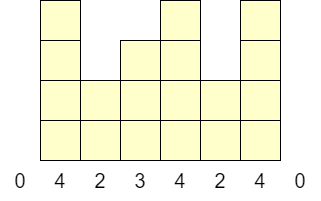
長方形領域 $[l,r] \times [0,h]$ について、
- $[l,r] \times [0,h]$ はヒストグラムに含まれる
- $[l-1,r] \times [0,h]$ はヒストグラムに含まれない
- $[l,r+1] \times [0,h]$ はヒストグラムに含まれない
- $[l,r] \times [0,h+1]$ はヒストグラムに含まれない
が成り立つとき、これを極大長方形ということにします。
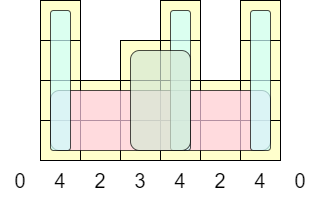
上の図では、$5$ つの極大長方形があります。
次が成り立ちます:操作回数の最小値 $=$ 極大長方形の個数
証明
数列をヒストグラムと見なすと、操作は、長方形の和集合により $A$ を作ることと言い換えられる。また、極大でない長方形を極大長方形に取り換えることで、極大長方形による被覆について考えればよい。よって、極大長方形のみを用いてヒストグラムを被覆するために、全ての極大長方形を用いる必要があることを示せばよい。
極大長方形 $[l,r] \times [0,h]$ に対して、上に伸ばせないことから、ある $i\in [l,r)$ が存在して $A_i = h$ が成り立つ。$[i,i+1] \times [0,h]$ を被覆する極大長方形が $[l,r]\times [0,h]$ のみに限られることを示せば、この極大長方形を用いる必要があることが示される。この領域を被覆する極大長方形の高さはちょうど $h$ でなければならないことから、極大長方形の一意性は容易に分かる。
$O(N^2M)$ 解法
すべての $A$ に対して、極大長方形の個数を足し合わせたものが答です。
長方形 $[l,r]\times [0,h]$ の寄与を考えます。これが極大長方形になるような数列 $A$ は次を満たすものです。
- 任意の $i\in [l,r)$ に対して $A_i\geq h$
- ある $i\in [l,r)$ に対して $A_i = h$
- $A_{l-1} < h$
- $A_{r} < h$
- これら以外の $A_i$ は何でもよい
これが成り立つ数列 $A$ の個数を $f(l,r,h)$ とすると、答は $\sum_{l,r,h} f(l,r,h)$ となります。
$l$ や $r$ が両端であるか否かによって、少し計算式が変わります。どちらも両端ではない場合($A_{l-1}$, $A_{r}$ が考えている範囲内に存在する場合)には、
- $[l,r)$ 内の決め方:$(M-h+1)^{r-l} – (M-h)^{r-l}$
- $A_{l-1}$ の決め方:$h-1$
- $A_{r}$ の決め方:$h-1$
- その他の $A_i$ の決め方:$M^{N-(r-l)-2}$
通りあって、$$f(l,r,h) = \bigl((M-h+1)^{r-l} – (M-h)^{r-l}\bigr)(h-1)^2M^{N-(r-l)-2}$$ となります。
$O(NM)$ 解法
$n = r – l$ ごとに集計すれば、$O(NM)$ になります。$f(l,r,h)$ の値は(両端が絡む場合を除き)共通なので、$(l,r)$ が何通りあるかをかけ合わせてまとめて計算できます。
冒頭にリンクした私の解法は、コード内で愚直解 → $O(NM)$ 解という順で記述しているため、困ったら見比べてみると良いと思います。

$O(M\log N)$ 解法
$\sum_{n=0}^{N-1} r^n$ や $\sum_{n=0}^{N-1} nr^n$ をまとめて $O(\log N)$ 時間で計算することで、全体として $O(M\log N)$ 時間でも計算できます。


