概要
シンプルな問題で、問題設定自体は自分でも考えたことがありました(この制約で解ける問題だとは思っていなかったです)。出題されて改めて考えてみると、上手く解けました。
解説の方法と違う方法だったので書きます。書くのは、サイクル類の長さの変化を列挙する部分です。
$O((N+Q)^{3/2})$ 解法
見出しの時点でもう読まなくても分かっちゃいそうですね。クエリ平方分割で解けます。
先に、いつもの計算量解析について述べておきます。適当なバケットサイズ $B$ をとり、$Q$ 件のクエリを $B$ 件のクエリ $\lceil Q/B\rceil$ 回に分けます。計算量解析は以下のようになります。
- あるバケットのクエリ処理の前に、計算量 $O(N)$ の前計算を行う
- 個々のクエリを計算量 $O(B)$ で処理する
すると、全体の計算量は $O\bigl(\lceil Q/B\rceil N + QB\bigr)$ となりますが、例えば $B = \sqrt{N}$ ととれば、これは $O(N + Q\sqrt{N})$ であることが分かります。
以下、バケットのクエリ処理に対する前計算と、クエリ処理について述べます。
$B$ 件のクエリを先読みすると、スワップされる可能性があるインデックス $2B$ 件以下を列挙できます。するとこの部分以外のインデックスはすべて、バケット内のクエリ処理の過程で不変です。したがって、順列を圧縮することができます。
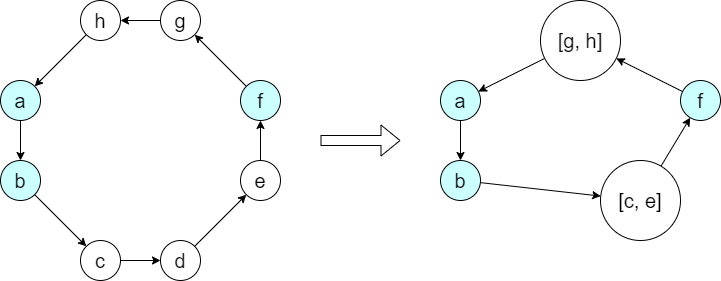
圧縮後のグラフの頂点について、 (head, tail, size) みたいな情報を持っておけばよいでしょう。
あとは辺を張り変えるたびに、サイクルの頂点をたどれば、サイクルのサイズを取得できます。これには圧縮後のグラフの頂点数 $O(B)$ に関する線形時間をかけて良いので、簡単です。
コメント
別の問題の解説でクエリ平方分割を見ていたときに、この問題も解けることに気づきました。
順列ではなく写像(functional graph)に対するクエリとかでも同じ要領で扱えますね。

