概要
問題文 → ■
公式解説 → ■
自分の提出 → 本番 ■, コンテスト後 ■
本番、計算式を間違えていて 1 時間消し飛んで、間に合わなくなってしまった。悲しい。
公式解説と違っていて、また同方針で解こうとしている方も居るようでしたので、書いておきます。公式解説の方が簡単で悔しい。
$O(H^2W^2)$ 解法
回数期待値の言い換え
まずは、DAG 上で終了状態と遷移確率が与えられて、「操作回数の期待値を求めよ」と言われた場合の典型的な言い換えです。
「操作回数の期待値」は、「操作を行うたびに $1$ 点獲得」として、合計点の期待値です。ひとつひとつの操作に分解して考えます。
操作が行われる始状態 $S$ ごとの寄与に分解して考えると、
- ゲームが終了していない各状態 $S$ に対して、状態 $S$ への到達確率を $p(S)$ とする。このとき、答は $\sum_{S} p(S)$ である。
と書き変えられます。(DAG に自己ループを加えた場合でも同様の考察は典型だと思います)
よって、$2$ マスともを含む長方形 $[xl,xr] \times [yl,yr]$ に対して到達確率を求めて足し合わせるという方針が可能です。
操作列について
- はじめに $N$ 個の選択肢がある
- 各時点で残っている選択肢の中から、等確率に選択肢を選ぶ
- 選んだ選択肢を含むいくつかの選択肢が消える
として得られる操作列の確率分布は、次のようにして得られる操作列の確率分布と等しいです。
- はじめに $N$ 個の選択肢に、独立に一様乱数により優先度を割り当てる
- 各時点で残っている選択肢の中から、優先度の最も高いものを選ぶ
各時点で、両者の選択の確率分布が一致していることが確かめられるでしょう。
到達確率の計算
$2$ つの黒マスを含む長方形への到達確率を求めましょう。

例えば図での長方形に到達する確率はどんなもんでしょうか?上で述べた「優先度」による解釈をすると、次のように言い換えられます。
- $x_1, \ldots, x_6, y_2, \ldots, y_7$ を、優先度が高いものから並べたときに、大きい方から $4$ つが $x_1, x_6, y_1, y_7$ の並べ替えである。
優先度は全ての選択肢に対して独立に割り当てられているので、優先度トップ $4$ としては全ての $4$ 元集合が等確率で現れます。したがって、上図の場合には、到達確率は $\binom{12}{4}^{-1}$ であることが分かります。
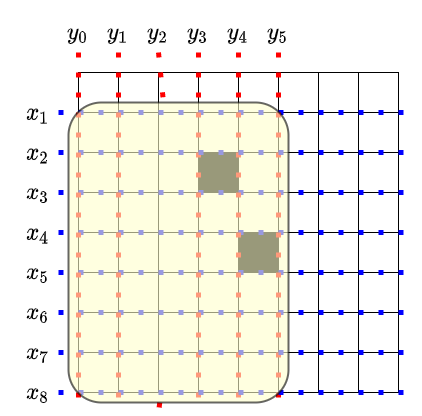
この図だとどうでしょうか?このように、元のグリッドの辺を境界とする長方形については、計算が少し変わります。
- $x_i, y_j$ のうちで、優先度トップ $4$ が $\{x_1, x_8, y_0, y_5\}$ である
- ただし、$x_8, y_0$ には $\infty$ の優先度が割り当てられている
と見なすと良いです。長方形の辺を除く $12$ 本の直線のトップ $2$ が $\{x_1, y_5\}$ であればよいです。到達確率は $\binom{12}{2}^{-1}$ です。
$O(H^2W^2)$ 解法
$2$ つの黒マスをともに含む長方形は、$O(H^2W^2)$ 通り存在します。これについて、上のように到達確率を計算して、足し合わせればよいです。
なお、私の AC コードのうち、sol1 関数がこの愚直解法を実装しています。

$O((H+W)\log(H+W))$ 解法
到達確率は、
- 長方形の縦 $+$ 横:$n$ 個
- $4$ 辺のうち、いくつが元の長方形の辺か:$k$ 個
としたとき、$n, k$ のみから定まります。同じパラメータ $(n,K)$ の寄与をまとめることを目指します。つまり、$(n,k)$ に対する長方形を数えたいです。
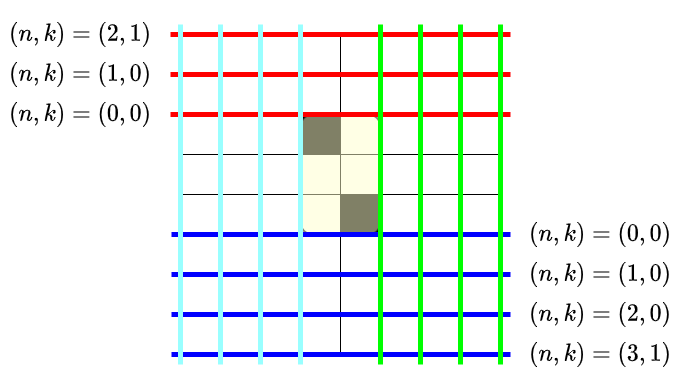
そもそも長方形は、いくつあるでしょうか?黒マスを含む長方形を定めることは、上辺・下辺・左辺・右辺をそれぞれ独立に選ぶことと対応します。よって、長方形の個数はただの掛け算、上の図だと $3\times 4\times 4\times 4$ 通りです(本番、このことにすら気づいていなかったな…)。
元から長方形の縦 $+$ 横 として$n = 5$ ある状態から、赤線のどれを選ぶか、青線のどれを選ぶかによって、$(n,K)$ が上の図のように加算されます。
したがって、$(n,k)$ ごとの数え上げを $f_{n,k}$ とすれば、これは多項式乗算
$\sum_{n,k} f_{n,k}x^ny^k = $ $(1+x+x^2y)$ $(1+x+x^2+x^3y)$$(1+x+x^2+x^3y)$ $(1+x+x^2+x^3y)$ により計算できます。
$y$ については低次なので、例えば $x$ についての積のみ FFT すれば、すべての $f_{n,k}$ が $O((H+W)\log(H+W))$ 時間で計算できます。
$O(H+W)$ 解法
$f(x,y) (1+x+\cdots+x^{n-1}+x^{n}y)$ の形の多項式乗算ができればよいです。$y$ について十分低次なので、$f(x,y) = \sum f_i(x)y^i$ と見なして、$f_i(x)(1+x+\cdots+x^{n-1})$ の計算および $f_i(x)x^ny$ の計算ができればよいです。
前者は $\frac{1-x^n}{1-x} = (1-x^n)\cdot \frac{1}{1-x}$ をかければよいので、係数ごとに $O(1)$ 時間です。後者もいうまでもなく、係数ごとに $O(1)$ 時間です。よって、これらは線形時間で計算することができます。
以下の解答例では、$(1-x^n) + (1-x)x^{n}y$倍してから $(1-x)$ で割る形で実装しています。


