概要
あまりスマートな解法ではないと思うのですが、解説を書いている方が居ないようだったので書いておきます。
実験、偶奇不変量の発見
私はまず、BFS で、$[1,2,\ldots,N]$ から操作で作れるパターンを全生成しました。$N\leq 10$ まで計算してパターン数を数え上げると、$1, 1, 6, 24, 120, 360, 5040, 40320, 362880, 1814400$ となっていかにもな予想が立ちます。
- $N\not\equiv 2\pmod{4}$ ならば、すべての順列がソート可能だろう
- $N\equiv 2\pmod{4}$ ならば、半数の順列がソート可能だろう
こうした実験・観察は解答への最短経路では不要な場合もありますが、誤った方向での思考を防ぐことができます。簡単なところでは、「十分大きな $N$ では常に構成可能であることを示そうとする」ことを防ぐことが出来ます。また、約半数の順列に対して解けるような構成方法を考えるだけでも十分役に立ちそうだと想定できます。
次の観察も、実験結果から容易に発見できます。
$N\equiv 2\pmod{4}$ のときは、どの位置の操作も偶置換である
成り立つことが発見できれば、証明は簡単です。
基本アルゴリズム
状態 $i$ を次のように定義します。
【状態 $i$】次のどちらかが成り立つこと。
・配列 $A$ の prefix が $i, i-1, \ldots, 2, 1$ である。
・配列 $A$ の suffix が $1, 2, \ldots, i$ である。
このとき、次が実現できます。
$i < N$ であるとき、状態 $i$ から $2$ 手以内に状態 $i+1$ にうつせる。
実際、次のようにすればよいです。$A$ の prefix が $i, i-1, \ldots, 2, 1$ であるとします。
[case 1] $i+1$ が右端以外の場所にあるとき
$k$ 番目にあるとして、$k, k+1$ の順に操作します。
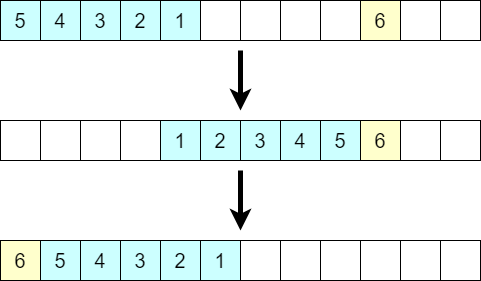
[case 2] $i+1$ が右端にあるとき
右端について操作すればよいです。

状態 $i$ のうち、$A$ の suffix が $1,2,\ldots,i$ の場合も同様です。
問題の解法
基本アルゴリズムにより、$2N$ 手以内に次のどちらかにうつせることが分かります。
- $1, 2, \ldots, N-1, N$
- $N, N-1, \ldots, 2, 1$
このことから、まず次が確認できます。
・$N\equiv 2\pmod{4}$ かつ $A$ が奇置換ならば、解くことは不可能である
・$N\equiv 2\pmod{4}$ かつ $A$ が偶置換ならば、$2N$ 手以内で解ける
・$N\equiv 1,3\pmod{4}$ のときは、$3N$ 手以内で解ける
・$N\equiv 0\pmod{4}$ のときは、$4N$ 手以内で解ける
$N\equiv 2\pmod{4}$ の場合について、どの操作も偶置換だったので、奇置換はソート不可能です。偶置換は基本アルゴリズムで $1,2,\ldots,N$ または $N,N-1,\ldots,2,1$ にうつせますが、はじめが偶置換ならば結果も偶置換です。
$N\equiv 0,1,3\pmod{4}$ とします。このとき、$N,N-1,\ldots,2,1$ を 次の要領で $1,2,\ldots,N$ にうつすことが可能です。
- $0, N-1$ に対して操作を行うと、$2$ つ cyclic shift することができる
- $N$ が奇数ならば、操作 $0$ で $N,1,2,\ldots,N-1$ にしたあと cyclic shift していけばよい。
- $N=2n$ が $4$ の倍数ならば、操作 $0,1,\ldots,N-1$ を順に行い $n+1,\ldots,2n,1,\ldots,n$ にしたあと cyclic shift していけばよい。
だいぶ良いところまでいきましたが、$N$ が $4$ の倍数のときだけ評価が足りません($10000$ 手以内におさまらない)。そこで、次のように考えました:
$A$ が十分ランダムであれば、基本アルゴリズムの結果として $1,2,\ldots,N$ および $N,N-1,\ldots,2,1$ が確率 $1/2$ ずつで得られるだろう。
実際、すべての順列 $A$ を考えて、状態 $0$ を prefix / suffix どちら側と見なすかの両方を考えると、結果が同数ずつであることは対称性から分かります。
結局次のようにして、AC を得ました。
- $9900 – 2N$ ステップ程度、ランダムに操作を行う
- 基本アルゴリズムを行う
- $N, N-1, \ldots, 1$ になってしまったらやり直す
「十分ランダム」な数列を得るためにどのくらいのランダム操作を行えばよいのか等きちんと考察を行ったわけではありませんが、まあいかにも正当な解法だと思っています。よければ詳しい証明を考えていただけると嬉しいです。
なお、これは $N$ が $4$ の倍数のときのために考えた方法ですが、それ以外の $N$ の場合もこの方法で解けばよいです。十分な回数の「やり直し」が生じたら打ち切るようにすると、$N\equiv 2\pmod{4}$ かつ奇置換の場合も対処できます。

