| A | B | C | D | E | F | |
| 問題文 | ■ | ■ | ■ | ■ | ■ | ■ |
| 自分の提出 | ■ | ■ | ■ | ■ | ||
| 結果 | AC | AC | AC | AC |
全体感想
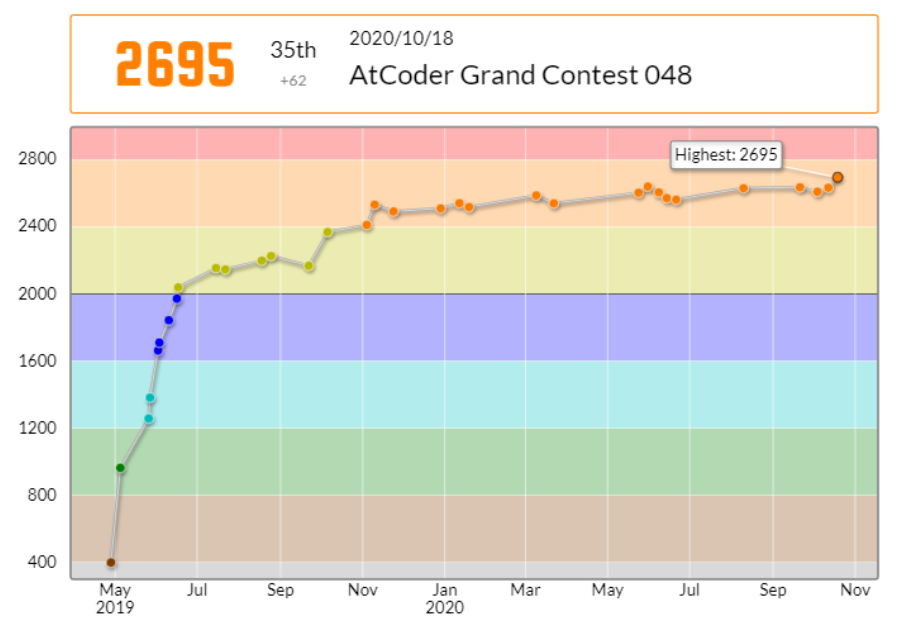
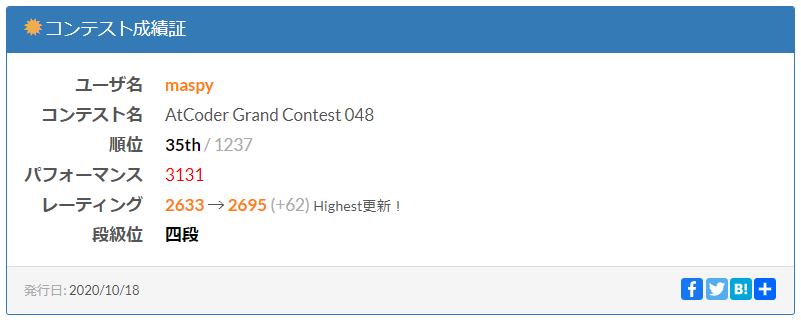
149分 2 ペナで、35 位でした。
いやー、良かった。本番で実装精度やデバッグ力が不足しているせいで「あと数十分あればなー」という結果に終わってしまうことが、最近多く感じられていたので、久しぶりに境界の良い側を引けて嬉しいです。

立ち回り。問題 A が遅いですが、これ本当に、他の問題文を一切見ずに問題 A をずっと解いていました。「きちんと序盤を解けば最低パフォは簡単に稼げる」という自身の学びを元に、序盤で方針が分かった問題はなるべくそのまま実装しきるようにしています。また、$300 + 700 > 900$ などから、問題 A を解かず後ろをやる利点が少なさそうだという判断もありました。
しかし…いやー、誤読に気を付けているんだけどな…。問題 A でやらかしました。(’agc’ より大きくする問題を解いていて、長さが短いことに基づく実装 → 実装方針から全部やりなおし。)地味に、AGC-A はひどいミスをしていることが多いです。
あとは、そもそも解法が冗長だったみたいで、実装量がわりと多くなってしまいました。
問題 B を 10 分くらいかけて解けず、問題 C は 5 分ほどで考察の起点を見つけたので、C から解き。B は難しそうなのにかなり AC が出ていてびっくり。少し実験すると良さそうな必要条件を見つけて、十分性の証明は簡単でした。
問題 D は分からなかったので E, F も読み、数分考えますが、問題 E は設定がなかなか頭に入ってこなかったので放棄。問題 F は設定はすぐ分かったけど、AC が居なかったので数分考えて放棄。既に AC のそこそこ出ていた問題 D に専念すると決めます。
数十分して良さそうな方針がひとつ立ちますが、想定解法と比べてかなり複雑な方針であったため、実装が結構大変になりました。40 分くらいかけて主要部を実装し終わった時点で、残り 10 分を切っていました。答が合わず…ひとつのバグはすぐ見つかったけど、まだ合わず…。見返すも分からない…。後回しにしていた入出力部分だけ作って…。
残り 5 分のうち、2 分ほどは、自棄になって適当に $+1$ をつけたり $\geq$ と $>$ を変えてみたりしてしまいました。最後の最後、もう一周 1 行 1 行確認していると…… AC!
いやー、嬉しかったです。(初めからバグらせないようにしなさーい案件ですが)
問題A – atcoder < S
公式解説と違う方法で解いたので、簡潔に。目標とする文字列の形を場合分けします。次のいずれかの形の prefix を作ります。
- (b 以上)
- a + (u 以上)
- at + (d 以上)
- atc + (p 以上)
- $\cdots$
- atcode + (s 以上)
- atcoder + (a 以上)
これらそれぞれに対して、可能かの判定および、操作回数の最小値の計算をすればよいです。
例えば「atc + (p以上)」を作る際には、
- 最も左にある a を採用
- 最も左にある t を採用
- 最も左にある c を採用
- 未採用の文字のうち、 p 以上のもので、最も左にあるものを採用
あとは、これらを左に移動させるときの転倒回数を計算すれば良いです。
問題B – Bracket Score
それぞれの括弧に対して用いる、添字集合しか関係ない(開括弧・閉括弧の区別が必要ない)ところはポイントになりそうです。開括弧の位置の集合として適切な添字集合の特徴づけを探します。
適当な必要条件を探します。とりあえず、偶数個の添字を選ぶことが必要だとわかります。長さ $4$ の文字列で特徴づけとの差を考えると、添字集合「0, 2」「1, 3」のようなものが上手くいきません。長さ $6$ の場合を色々書こうとしても、大体同じで、上手くいっている状態あらひとつ座標を変えたりすると、上手くいかなくなります。いったん偶奇性に注目しようという気持ちになります。
長さ $2n$ のマス目を、 $2$ 色に塗り分けてながら、いろいろ括弧を書き込んだりして考えます。対応する開括弧・閉括弧の間には偶数文字が入るはずで、これらは添字が (偶数, 奇数) または (奇数, 偶数) となっているはずで、ここから、
- 必要条件:全体で、添字が偶数のもの、奇数のものを同数用いる必要がある
を見つけます。これが十分条件かどうかはよくわからなくて、適当に奇数・偶数の添字をマッチさせるだけでは詰む場合:添字集合 1, 3, 4, 6 で (1,4) をペアにしてしまう場合などを見つけましたが、これを観察しながら十分性が証明できました。
累積和の意味で奇数・偶数の添字の個数が等しくなるところで $1$ 文字目とマッチさせれば、以下再帰的に括弧列を復元する方法の存在が確かめられます。
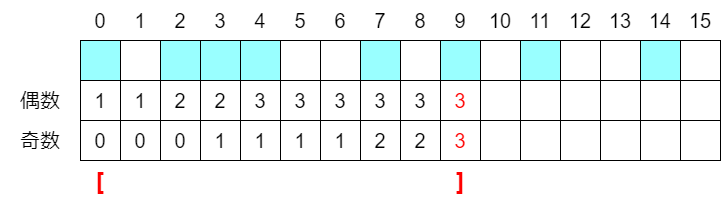
実験、偶奇性。手段が全然見つからない場合には、愚直解法で調べる添字集合を生成してみたり、それを数え上げたりしてみるのも有効だと思います。何か必要条件を思いついたら、必要条件と、実際の考察対象の差集合を愚直生成してみるという方法をとることもあります。
問題C – Penguin Skating
これは数分で一番大事なところに気づけた。
数列の操作で、少し変数変換すると見やすい操作になるというのは大事な典型ですし、累積和や差分に取り換えるというのもよくあると思います。差分に注目してサンプルを可視化しました。

差分に注目するのですが、座標の差分というよりは、$1$ を引いて間にある空マスの個数に注目してあげた方が分かりやすそうだったので、そのようにしました。操作は、
- $(\ldots, a, b, \ldots) \to (\ldots, a+b, 0, \ldots)$
- $(\ldots, a, b, \ldots) \to (\ldots, 0, a+b, \ldots)$
のどちらかです。この過程で作れる数列がどのようなものかを考えると、$0$ を無視すれば、もとの数列を分割して区間ごとにマージしたものに限られることが分かります:
$$(0, 2, 1, 3, 1) \to (021 | 31) = (3,4) \to (0,3,0,4,0)$$
これで判定問題が解けました(うっかり、判定だけを一度実装してしまい、時間をロスしました)。
あとは最小回数です。判定問題は私は $0$ を無視することによって考えたのですが、移動回数については $(a,0,0)$ と $(0,a,0)$ などは区別が必要なので、もう少し捉え直します。単に「隣接 $2$ 数のマージ」と認識するのではなく、「ある位置にある空マスを、すべて左または右に移す」と捉える方が良さそうです。
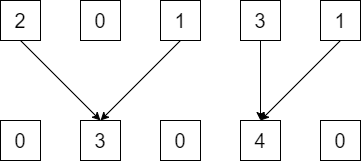
あとは、同じマスに移動させる数は、まとめて動かしても良いことに注意すれば、簡単に答が計算できます。
問題D – Pocky Game
想定解よりは少し複雑な、考察・実装になってしまいました。
ゲームの戦略・勝敗は、通常ゲームの終盤から順に確定できるものなので、まずは、$1$ 山、$2$ 山、$3$ 山と順に考察しました。
$1$ 山だと全部とって先手勝ちです。Nim とも完全に別ゲーであることが分かります。$2$ 山だと、自分の手番で残り $1$ 山に持ち込んだ人が負けるため、手元の山の大きさの大小対決であることが分かります。$3$ 山も、どういう状態になれば $2$ 山に持ち込んで良いかを考えれば計算できそうですが、ちょっとややこしそうだったので、いったん別の考察方法にうつりました。
制約について考えます。$O(N^2)$ や $O(N^3)$ で解ければ良さそうです。また、ゲームの途中経過としてありうる状態は、
- 「先手が山 $L-1$、後手が山 $R+1$ に着手していて、$L$ から $R$ の山が丸ごと残っている」
という状態に限られるので、それを利用して区間 $(L,R)$ またはそれに $1$ 次元分余分な情報を持たせて dp できると良いのかなあとは初期に考えていました。
愚直解法を実装しました。(超有名な Nim の時点で割とそうだと思うのですが、ゲームの問題では、実験して予想しないと、勝利条件の導出や証明が困難。逆に予想できれば証明は簡単。という場合は多いように感じています。)

ある状況が先手勝ちならば True, そうでなければ False を返します。ある状態からの遷移先に、必敗状態があれば先手勝ち。必勝状態しかなければ先手負け。などとなります。メモ化再帰による実装が、そこそこお手軽です。(はじめ、True, False のみの実装としていましたが、途中で勝つための戦略のひとつをかえす実装へ変更しました。出力の正しさの確認や、理解のためにやくにたちました)
これで、実験し放題になりました。$3$ 山や $4$ 山の勝利条件をいろいろ可視化できます。
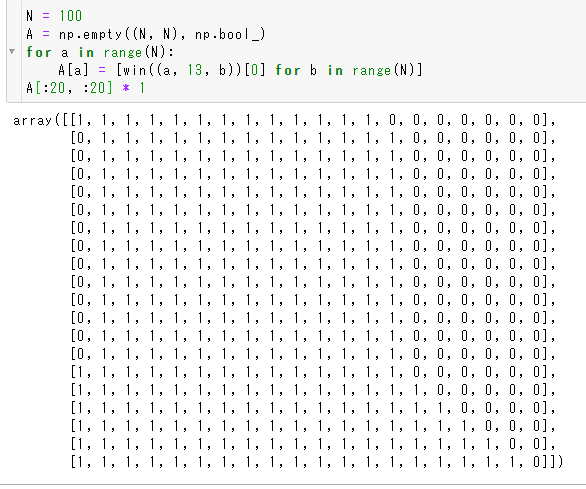

こういう感じの可視化をしながら、実験しました。$3$ 山の場合の勝利条件の形は何となくわかったので、さらに $4$, $5$ 山も両端を $2$ パラメータとして $2$ 次元に可視化していきます。乱数でデータを作って、何回も可視化してみました。

どうやら、次が成り立ちそうです。
任意の数列 $A_1, A_2, \ldots, A_n$ に対して、ある数 $p, q$ が存在して、次が成り立つ:$$ゲーム (a, A_1,A_2,\ldots, A_n, b) が後手必勝 \iff b \geq p \ \text{and} \ b – a \geq q$$
区間 $(A_1, A_2, \ldots, A_n)$ の状態を $2$ 整数で表現できそうなので、あとは、dp を使ってこの $p, q$ を小さい区間から順に計算出来れば良さそうです。この辺までで、「あとは時間との勝負だなー」という気持ちになりました($3$ 山の場合ですら一度立式をあきらめたので、短時間で詰め切る自信はあまりなかった)。
より小さい区間で $p, q$ が計算されているとして、大きい区間の場合を考察します。

区間 $[L, R]$ の両端の数が $X$, $Y$ であるとします。さらにその外側に、各プレイヤが着手中の山が $a$ 個、$b$ 個で残っているとします。
- 区間 $[L+1,R]$ の計算結果と $X$ の値
- 区間 $[L,R-1]$ の計算結果と $Y$ の値
から、どちらかが山を取りきった瞬間にのこりの勝敗が決定できることが分かります。つまり、このゲームは、適当な $a_0, b_0$ に対して
- どちらかが山を取り切った瞬間に、勝敗判定が行われるゲーム。
- 先手が山を取り切った時点で、$(後手の山)\leq b_0$ になっていれば先手が勝ち。
- 後手が山を取り切った時点で、$(先手の山)\leq a_0$ になっていれば後手が勝ち。
というゲームへと書き換えられます。あとは、$a_0,b_0$ を計算すればロジックが完成です。
実装がややこしい要素として、先手の $[L,R]$ に対する必勝条件を調べるために、上の $b_0$ を計算しますが、そこでは後手の $[L,R-1]$ に対する必勝条件を計算できている飛鳥があります。一度、ここも単に $\dp[L,R-1]$ の値を使っていて失敗しました。
先手、後手の必勝条件 $p,q$ を計算し続けていかなければなりません。残り $20$ 分ほどで、これを修正する必要があり、コピペして注意深く数式を修正できる自信がなかったです。そこで、上手く $2$ 回の実装をまとめる方法を考えました。

数列、dp テーブルに加えて、逆から見た数列、その場合の先手必勝条件の dp テーブルを持ちます。これらを入れ替えて $2$ 回計算することで、$2$ 種の実装をまとめることができます。この辺は普段の練習の経験が活きましたね。短時間で修正できてよかった。
$<$ と $\leq$ などを間違えやすい微妙な計算が多くて、これ以外の部分でも実装ミスをしてしまっていましたが、ぎりぎりデバッグしきれて 149 分での AC となりました。
公式解説の方法、確かに…。はじめに「途中経過は $(a, A_L, \ldots, A_R, b)$ の形」という観察をしてしまい、可視化も 2 次元で行っていたので、かなり自然にややこしい解法に行ってしまいました。
途中経過として、必ず $(a, A_L, \ldots, A_R)$ とか $(A_L, \ldots, A_R, b)$ を通ると思えば解説の方法になるんだなあ。

