| A | B | C | D | E | F | |
| 問題文 | ■ | ■ | ■ | ■ | ■ | ■ |
| 自分の提出 | ■ | ■ | ■ | ■ | ■ | ■ |
| 結果 | AC | AC | AC | AC | AC | AC |
全体感想
26分全完で、2位でした。
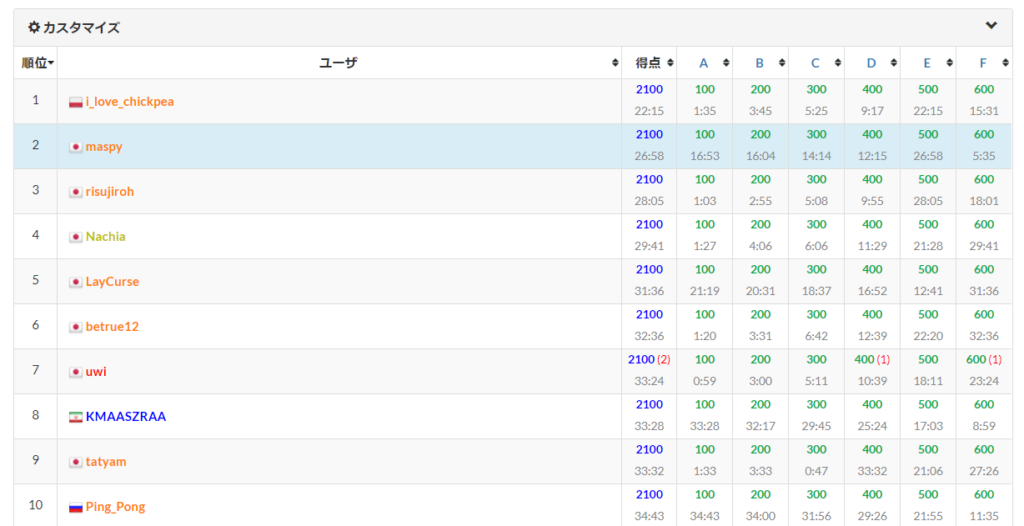
なんとなんと、2 位でした。最高順位更新、びっくりしています。
実装が遅い?苦手?とか、瞬発力では若者に及ばない?とか考えてしまうこともありましたが、何だかんだ実装スピードは速くなってきたみたいです。考察はまだまだ、ゆっくり考えてしまうことが多いですが、ABCコンテスト級なら反応が速くなってきたかしら?(過去問を進める速度は、考察スピードというよりも、布団や風呂の中など任意時間に考察をする能力で補われていると思います)
演習量ゆえの成長だと前向きにとらえていきます。
今回からこのような注意書きが表示されるようになりました。皆さん、お気をつけください。
今回の立ち回り:
1分遅刻。Fが簡単なので解く。Eを読んで、慎重さが必要そうなので後回し。DからAまで解いたあと、E。
問題Dはわりと好きです。ABCコンテストも算数数学に寄りがちと評価されることも多いですが、これはまさにアルゴリズム問題という感じですかね。
問題D – Lunlun Number
$K$ はそんなに大きくないので、検索対象の数だけを生成していくことができれば勝ちだなと、勝利条件を設定します。$k$ 桁のルンルン数は $k-1$ 桁のルンルン数に $1$ つ付け加えればよいので、桁数の小さいものから順に作っていくことができます。左側、右側どちらに追加してもよいですが、右側の方が数式が桁数に依存しないため、易しいと思います。
最後にソートして $K$ 番目を答える…と思っていたら、この生成順だと勝手に小さいものから生成されてくれました。
$k$ 桁の場合から、だいたい $3$ 個ずつ $k+1$ 桁のものが生成されるので、$k$ 桁のルンルン数は だいたい $3^k$ のオーダーで存在しそうです(厳密なことではなくて、かなり大雑把な話)。ここから $10$ 桁前後まで作ればよいかなと思い、実際に作ってみながら調整しました。手作業で調整してしまいましたが、$10^5$ 件を超えたらループを打ち切るような仕掛けを実装する方が手早かったのが反省です。また、「入力例4」を観察するという方法もあります。
問題E – Yutori

図にあわせて、労働を赤い辺と呼びます。期間内に $K$ 回以上の赤い辺を回収せよという問題です。
DAGなので dp が使えて、各頂点までに / 各頂点から先で とれる辺の個数の最大値が評価できます。
頂点 $v$ での労働を禁止した場合の最大の労働回数は、$v-1$ までの最大回数、$v+1$ からの最大回数を足せば計算できるので、個々の判定ができます。
問題F – Division or Substraction
「操作」に選択肢もなく、$N$ から終了状態が一意に定まります。まずはこれを理解します。
$N = K^eM$ (ただし $K\nmid M$) としたときに、まず $N$ が $M$ になります。そのあと $K$ を引けるだけひくので、剰余 $M \% K$ が残ることが分かります。
操作が理解できたので、次に、操作結果が $1$ になるのはどういうときかを考えます。数式で書けるときは、なるべく数式にすることを心がけています。$N = K^e(aK+1)$ と書けるときだと分かります。
ここから、$K$ は $N$ または $N-1$ の約数であることが必要だと分かります。個々の約数に対する判定も この式から簡単に行えます。約数の生成は、$\sqrt{N}$ まで試し割りをすればよいです。より優れた方法もありますが、AtCoder の公式コンテストで要求される場面は私は見たことがありません(プライベートで必要になったときは、sympy.ntheory の助けを借りて済ませることが多いです)。

