| A | B | C | D | E | F | |
| 問題文 | ■ | ■ | ■ | ■ | ■ | ■ |
| 自分の提出 | ■ | ■ | ■ | ■ | ■ | ■ |
| 結果 | AC | AC | AC | AC | AC | AC |
全体感想
42 分 0 ペナ → 66位。先週に引き続きいまいち。
問題F:概要は数分で分かったけど、細部に自信が持てず、あとまわし。コンテスト後に振り替えると、5分で解き終わっても全く不思議ではないくらいに感じるのに…。なんか混乱してしまいました。
問題D:また形式的べき級数だー。と思って解きました。全完した後に、累積和も同時に持つだけだと気付きました。(まあいいか)
問題C – A x B + C
「$A$ を固定して数える」「$B$ を固定して数える」「$C$ を固定して数える」みたいな考え方をすれば、解法に行き着くと思います。
$C$ を固定して数えようと思うと、約数の数え上げが必要になります。$N$ 以下の自然数すべてに対する約数の個数の数え上げは、とても簡単な方法で $\Theta(N\log N)$ 時間、少し頑張ると $\Theta(N\log \log N)$ 時間などで計算できます。
$\Theta(N\log N)$ 時間で約数テーブル:https://atcoder.jp/contests/abc179/submissions/16878726
$\Theta(N\log\log N)$ 時間で約数テーブル:https://atcoder.jp/contests/abc179/submissions/16879653
本問では、$A$ を固定して数える方が簡単です。$B$ を決めれば $C$ は自動的に決まるため、$AB < N$ を満たす $(A,B)$ を数える問題になります。$A$ ごとに、このような $B$ の個数は $\lfloor \frac{N-1}{B}\rfloor$ と求まるので、これを足し合わせて $\Theta(N)$ 解法が得られます。
さらに本問は、$\Theta(\sqrt{N})$ 時間で解くこともできます。次が解ければよいです。
$AB < N$ となる自然数の組 $(A,B)$ を数え上げよ。
これを、「$A$ ごと」「$B$ ごと」といった場合分けをするのではなく、「$\min(A,B)$ ごと」という場合分けを利用します。$\min(A,B) = x$ となるような組 $(A,B)$ は、
- $(x,x)$
- $(x,y)$ ただし $x < y \leq \lfloor\frac{N-1}{x}\rfloor$
- $(y,x)$ ただし $x < y \leq \lfloor\frac{N-1}{x}\rfloor$
のいずれかの形をしていて、$x$ ごとに $\Theta(1)$ 時間で数え上げられますし、$x \leq \sqrt{N-1}$ までを調べればよいので、全体として $\Theta(\sqrt{N})$ 時間になります。
提出:https://atcoder.jp/contests/abc179/submissions/16881691
問題D – Leaping Tak
形式的べき級数を用いた考察を紹介します。
$f = \sum_{k}\sum_{L_k\leq i\leq R_k} x^i$ とします。このとき、$k$ 回の移動で $N$ 歩進む移動方法の数は、$[x^N] f^k$.$k$ を動かして足し合わせると、$[x^N]\frac{1}{1-f}$ となります。
形式的べき級数の逆元を上手く計算すれば、これは $\Theta(N\log N)$ 時間で計算できます。(参考:https://judge.yosupo.jp/problem/inv_of_formal_power_series)
まぁそんなのは ABC コンテストでは出ません。もう少し考察で簡略化しましょう。
今回の $f$ は、密な多項式ですが、$x^{l} + \cdots + x^{r} = \frac{x^l – x^{r+1}}{1-x}$ を利用することで、$f$ あるいは $\frac{1}{1-f}$ を疎な有理式として表すことができます。
$F = (1-x) f = \sum_{k}(x^{L_k} – x^{R_k+1})$ とします。これは $2K$ ($\leqq 20$) 個しか項を持たない、疎な多項式です。$f = \frac{F}{1-x}$ であり、$\frac{1}{1-f} = \frac{1-x}{1-x-F}$ は疎な多項式を分子・分母に持つ多項式です。ここから、$[x^n]\frac{1}{1-f}$ に関する疎な線形漸化式が得られ、問題を解くことができます。
より詳細には、$$a_n = a_{n-1} + \sum_{k} (a_{n-L_k} – a_{n-R_k-1})\qquad (n\geq 2)$$ という形の漸化式になります。また私は、$\frac{1}{1-x-F}$ を計算してから最後に $1-x$ をかける形で実装しました。
問題E – Sequence Sum
こういうのはまぁ、どこかから周期数列になります。適当な形に一般化するならば、例えば、
有限集合 $A$ および写像 $f\colon A\longrightarrow A$ がある。$a \in A$ を適当にとり、数列 $\{a_n\}$ を $$a_0 = a,\qquad a_{n+1} = f(a_n)$$ により定める。このとき、数列 $\{a_n\}$ はどこかから先は周期的である。つまり、ある $k, p$ ($p>0$) が存在して、$$i\geq k\implies a_i = a_{i+p}$$ が成り立つ。
といった主張が成り立ちます。
- $A$ の有限性より、$a_i = a_j$ となる $i < j$ が存在する。
- 一度 $a_i = a_j$ になれば、以降 $a_{i+1} = a_{j+1}, a_{i+2} = a_{j+2}\cdots$ も成り立つ。
などとして証明できます。途中から周期に入る様子は、しばしばギリシャ文字の $\rho$ に例えられ、$\rho$ 法というアルゴリズムの由来にもなっています。
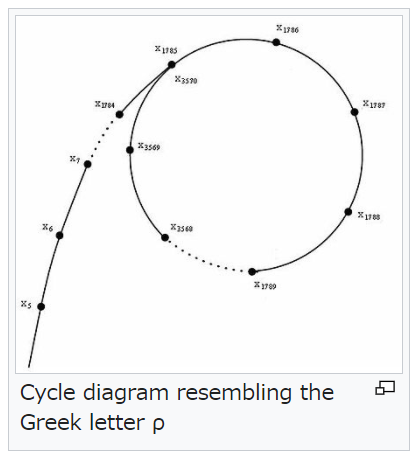
私は各 $k$ に対して、$A_n = k$ となる最小の $n$ をメモしていく形で実装して、周期に入るタイミングと周期の長さの検出をしました。周期に入るタイミングについては、最小のものを見つけなくても計算できますから、例えば「$A_n = A_M$ となる最小の $n > M$ を探す」→「$M$ 以降で周期 $n-M$ がある」などと、周期の開始地点を決め打ってしまってもよいです。
有限集合 $S$ が巨大な場合で、メモリを使わずに周期を発見する方法として、$A_n$ と $A_{2n}$ を計算していきながら $A_n = A_{2n}$ になるかを判定するという方法もあります。
- $a = b = A_0$ とする。
- $a ← f(a)$, $b ← f(f(b))$ と更新していって、$a=b$ になるまでに $n$ 回かかったとすると、周期 $n$ がある。
問題F – Simplified Reversi
各クエリでの塗りつぶし方を求めていきます。
あるタイミングで、縦方向の座標 $x$ にクエリが来たとします。このとき、どこまで裏返せるでしょうか?
同じクエリは二度来ないということなので、裏返す障害(初めての白マス)があるとしたら、それは横方向のクエリの影響です。したがって、これまでの横方向で裏返した位置さえ覚えておけば、これは計算できるということになります。より詳細には、横方向に $x$ 枚以上裏返したことがあるような行番号のうち最小のものが分かれば良いです。
したがって、
- 各クエリで裏返した枚数を、縦・横方向それぞれ記録していく。
- 次の枚数は、それらの記録されている値の区間最小値をとることで計算できる。
ということが分かります。セグメント木を 2 つ持てば計算できます。

