| A | B | C | D | E | F | |
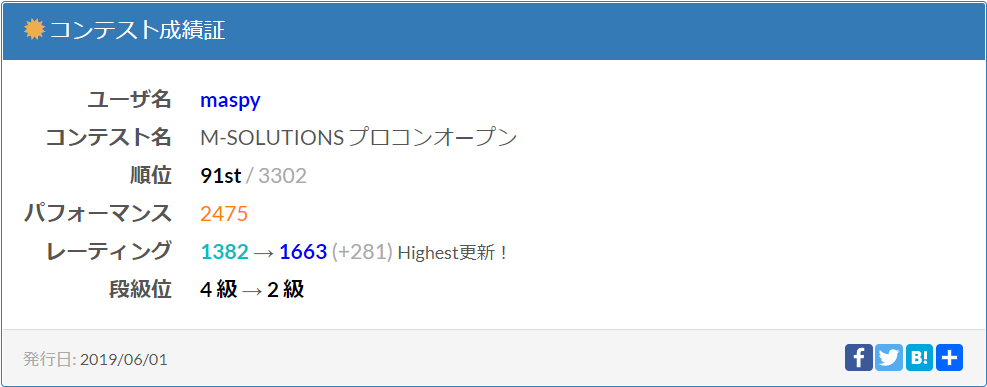
| 問題文 | ■ | ■ | ■ | ■ | ■ | ■ |
| 自分の提出 | ■ | ■ | ■ | ■ | ■ | |
| 結果 | AC | AC | AC | AC | AC |
全体感想
数学寄りのセットだったこともあり、比較的良い出来だったように思います。
これまでは解けたと思ってもバグ取りが終わらず点数に繋げられない回が多かったのですが、今回は大きな事故もなく順調に分かった問題を点数に結び付けられたという意味で、順位とは関係なく気分的に満足です。
問題Cは、恐らく競プロ界隈での典型的な出題形式に慣れていなかったことが原因で、上位層が省略しているであろう部分の考察に相当な時間を費やしてしまいました。つまり練習していけばまだ上に行けるということになりますね。少しずつ上達していこう。
問題B – Sumo
$8$ 勝できる可能性があるかを判定する。残り試合分、勝率数を上乗せした後判定する。
残り試合数を数えず、敗北数だけに注目してもよいようです。
pythonで、部分文字列のカウントは、.count()メソッドで行うことができます。
問題C – Best-of-(2n-1)
ゲーム終了までに $n$ 勝、 $m$ 勝必要だとして、ゲーム回数の期待値を$E_{m,n}$とします。$m,n\geq 1$のときに
\[ E_{m,n} = 1 + \frac{c}{100}E_{m,n} + \frac{a}{100}E_{m,n-1} + \frac{b}{100}E_{m,n-1}\]
が成り立つことがすぐに分かります。$E_{m,n}$の計算量が$O(mn)$となり、本問題は解くことができません。「漸化式を解く」必要がありそうです。移行して定数倍すると
\[ E_{m,n} = \frac{100}{a+b} + \frac{a}{a+b}E_{m-1,n} + \frac{b}{a+b}E_{m,n-1}\]となり。高校数学での漸化式の扱いと同様なテクニックがあれこれ利いて、最終的には
$F_{m,n} = F_{m-1,n} + F_{m,n-1}$という型の漸化式に帰着できます。よって$F$は二項係数の平行移動の重ね合わせとなり、漸化式を解くことができます。(適切な$k$に対して$G_{m,n} = E_{m,n} – k(m+n)$の漸化式を作ると定数項が消せる。さらに添字が$1$変わるたびに定数倍入るので、$F_{m,n} = \frac{(a+b)^{m+n}}{a^mb^n}G_{m,n}$と置けばよい。)
ここから、既約分数表示を求めるところで頭を悩ませます。初めは「出題からして、明示公式が作れば約分できないことが明白になるのだろう」とか思っていたけど、どうも約分についての評価が全くできません。多倍長整数として分数を計算しようとすると、$(a+b)^{m+n}$のような巨大すぎる大きさの分子・分母が出てきてTLE / MLEでしょう。
難しすぎ?? → 別の問題を解いたあと、もっと易しく解ける仕組みがあるはずだと思い再考。
よく考えると、約分の影響は無視できます。$p = 10^9+7$として$P = QR\pmod{p}$と解くだけですので、$P, Q$が定数倍ずれても問題ないです($Q$が$p$で割れるときだけ例外)。
これに気づいて気が楽になったのか、明示公式を作る部分についてもよりシンプルな方法が見つかります。$100$回に$a+b$回だけ状態が遷移するので、引き分けがないとして解いて答を$\frac{100}{a+b}$倍すればよいです。実際に漸化式をいじっているとき、途中からはほとんど$\frac{a}{a+b}$, $\frac{b}{a+b}$という分数を触っていました。
この2つの気づきを得られれば、後は自然に$O(N)$になりました。
解説では、「約分は無視できる」という要素について完全スルー…おそらく典型的な出題形式なのでしょうw
ここにずっと苦しめられたよ…経験不足ですね。覚えとこ。
———-
後日気づいたことですが、そもそも「分子と分母を求める」必要すらありませんね。次のような環準同型(和・差・積を保つ写像)があります。\[ \mathbb{Z}_{(p)} = \biggl\{\frac{m}{n}\biggm|m,n\in\mathbb{Z}, p\nmid n\biggr\} \longrightarrow \mathbb{Z}/p\mathbb{Z}. \]より専門的には、整数環$\mathbb{Z}$の素イデアル$p\mathbb{Z}$による局所化からの$\bmod p$還元写像。この対応は環準同型なので、数を(分子, 分母)の形で持つ必要は一切なく、分数が出てきたら順次$\mathbb{Z}/p\mathbb{Z}$に移しておけば問題ないです。
問題D – Maximum Sum of Minimum
簡単そうに見えましたが、具体例を紙で検証している最中に「あれ?最小値だっけ最大値だっけ?」みたいなことを繰り返したため、いったん後回しにしましたw
次数1の頂点については、その頂点の書き込み方さえ決めてしまえば、残りの頂点の書き込み方・得られる得点は完全に大きさが1つ小さいときの問題として扱えそうです。
小さい数は端に置きたいとは自然に思えたため、このことと組み合わせて証明を考えます。
「木の次数$1$の点に最小値を書いた方が得(書いても損をしない)」
「そのときのminの合計値が、$c$の小さい方から$N-1$個の和に等しい」
ことが帰納的に分かります。帰納法による証明によくあることですが、成り立つべき命題さえきちんと定式化出来てしまいさえすれば、証明自体は易しかったです。
個人的にはCよりも易しい問題でした。
問題E – Product of Arithmetic Progression
シンプルな整数論の割に、見たことはない。一応「等差数列の積・アルゴリズム」とかその英語でgoogle検索するも、パッとは見つからずw
「長さ$2^k$のものだけ事前計算してはどうだろう」「始点が$d$未満のときだけでよい」など考えたけれど、必要な事前計算が$O(N^2)$になってしまう($N=100003$)。
少し発想を変えてみる。そもそも$d=1$を解かなければいけない。つまり階乗は全部分かる必要がある。$n!$を事前計算なしに効率よく求める方法、あるいは事前計算を大幅に抑える方法は聞いたことがない。つまり大なり小なり、階乗の一覧あるいはそれに準ずる何かは作る必要があるだろう。
この時点でかなりきつい。階乗をひととおり作るだけで$O(N)$あるので、せいぜいそれの定数倍、$\log(N)$倍の類の事前計算で精一杯。つまり解けるとすれば、階乗だけ事前計算をして、それを上手に使うくらいしか方法がないだろう。 → 分かった!!
「解法があるとすれば」という逆算の発想で、偶然思いつけたというよりも、ある意味では「思いつくべくして思いつけた」という自己評価。
なるほどー。綺麗な問題ですね。

