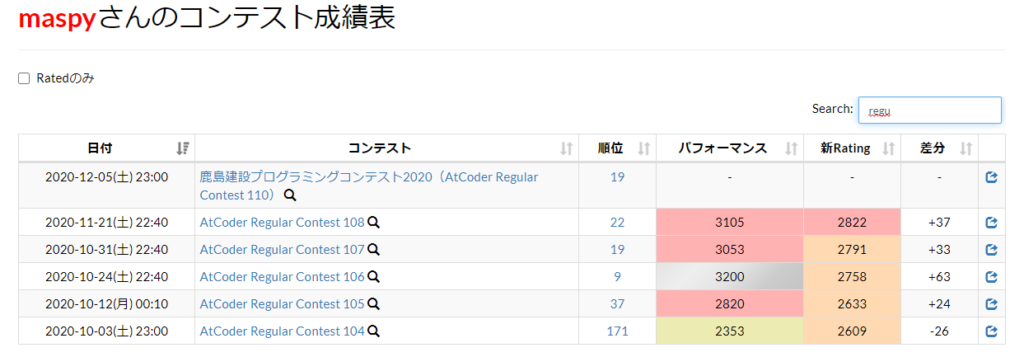
| A | B | C | D | E | F | |
| 問題文 | ■ | ■ | ■ | ■ | ■ | ■ |
| 自分の提出 | ■ | ■ | ■ | ■ | ■ | |
| 結果 | AC | AC | AC | AC | AC |
問題E コンテスト後AC → https://atcoder.jp/contests/arc110/submissions/18601542
全体感想
75分5完2ペナ、19位の成績でした。赤になったので ARC は unrated なのですが、パフォ 3000+ 相当あるようで、なかなか良い出来だったみたいです。
今の ARC 難易度帯、混戦の速度勝負になりそうで、良い結果が安定して出せないと思っていたのですが、今のところ予想に反して上手くいっています。(スーパー上振れて偶然赤になったような気もしていますが、再現性がいくらかあるようで安心)
早起きから朝から出かけていて、寝不足。仮眠から 20:50 起床。コンテスト開始直後から、腹痛で 10 分くらい離席するなど、序盤コンディションかなり悪い感じでしたが、何とか。
問題B – Many 110
T = S[i:i+N] となる $i$ を数える問題です。これを、$i\pmod{3}$ で場合分けして調べました。$T$ の構造で場合分けする方針だと $N = 1$ の場合にコーナーケースになったりするようですが、私の方針だと特にコーナーケース対応は必要なかったです。
問題D – Binomial Coefficient is Fun
数え上げがこれだけ出題されるコンテンツですし、数え上げ分野においては形式的べき級数といえば、専門書では真っ先に解説されることも珍しくない代表手法ですから、特に不自然な偏りではないと思いますが。過去問と比べてもやや増加してはいるっぽい?

$B$ の和ごとに状態を持たせたいので、次の $f_i$ を考えます。$$f_i = \sum_{b=0}^{\infty} \binom{b}{a_i} x^b.$$
すると、$F = f_1f_2\cdots f_N$ における $1, x, x^2, \ldots, x^M$ の係数の総和が求めるものです。あとは少し基本的な式変形をします。
固定された $a$ に対して $\binom{n}{a}$ が係数に並ぶ形式的べき級数としては、負の二項定理 $$(1-x)^{-(a+1)} = \sum_{n=0}^{\infty} \binom{n+a}{a} x^n$$ があります。$f_i = \frac{x^a}{(1-x)^{a+1}}$ とすればぴったりです。$F = f_1f_2\cdots f_N$ はこれらの積なので、$A = \sum a_i$ として、$F = \frac{x^A}{(1-x)^{A+N}}$ となることが分かります。これの $0, 1, \ldots, M$ 次の係数の総和が知りたいですが、係数の累積和を得ることが $(1-x)$ で割る操作と対応することを思い出すと、答は $ [x^{M}] \frac{F}{1-x}$ です。
以上を合わせて、答は
$$[x^M]\frac{x^A}{(1-x)^{A+N+1}} = [x^{M-A}] \frac{1}{(1-x)^{A+N+1}} = \binom{M+N}{A+N}$$
であることが分かります。
$\sum$ の範囲など微妙に気になりますが、$0 < n < k$ や $k < 0 < n$ に対して $\binom{n}{k} = 0$ であることなどを合わせると、二項定理 $(1+x)^d=\sum_{n=0}^{d}\binom{d}{n}x^ny^{d-n}$ や負の二項定理 $(1-x)^{-d} = \sum_{n=0}^{\infty}\binom{n+d-1}{d-1}x^n$ の類は和の範囲を広げても正しいので、割と適当に扱って上手くことが多いですね。
問題E – Shorten ABC
最後の詰めが大変で、結構解くのに時間がかかりました。考察手順について少し書いてみます。
こういうのは、発想が必要と言われがちだと思うんですけど、考察の方向性は典型ですし、アドホックな発見が必要なところも全探索による実験と観察を繰り返せば、意外と運に頼らず着実に解ける問題だと思います。以下のような問題で、同種の経験がありました(結果は違えど考察の方向性や手順は似たものだった)。
数え上げ対象は操作の結果です。操作にかなり自由度がある結果を数え上げる場合、まずはどのような結果が構成可能かを判定する方法について考察することになります。(多くの操作列から同じ結果が構成できる場合、判定問題に対する考察を経由せずに数え上げが行える問題ことはほとんどないと思います)。まずは数え上げを離れて、思考を判定問題に向けます。
今回の問題は、複数の文字を $1$ 文字に置き換えていくタイプです。このような場合、変換後の文字ひとつひとつがその順番通りに元の文字列の部分文字列(区間)と対応して、文字列の構築を $1$ 文字 $1$ 文字に分解して独立にとらえることができます。
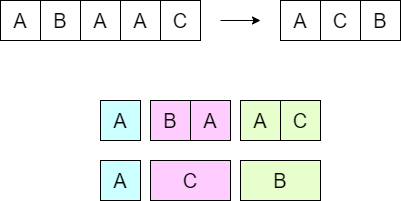
したがって、ある文字列が元の文字列から作れるかを判定するにあたって、
ひとつの文字が、どのような文字列(元の文字列の区間)から構成可能か?
を考えると良さそう気がします。これは、「この考え方を経由すると判定問題が解けることがある」という、ある意味では問題に対して十分な考察です。一方、いろいろな文字列に対する判定問題が解けるとすると、少なくとも $1$ 文字の文字列に対する判定問題は解けることになるため、判定に際して必要な考察であることも分かります。よってこの課題に取り組むことが問題を解く上で役に立たない可能性はきわめて低いという安心感があります。
あとは、頑張って必要条件や十分条件を探していきます。課題を「$1$ 文字に対応する文字列」に絞っているおかげで、全探索を利用した愚直パターン生成が簡単に行えます。
操作を遡る要領で生成しました。(このへんの実装も、 AC コード内にも残してあります)
あとは、ひたすら実例を見ながら必要条件を探したり、十分条件を探したり、それと実際のパターンとの差分を改めて観察することを繰り返していきます。解法がパッと思いつかなくても、色々できることはあると思います。
全パターン生成を実装しておくと、必要条件や十分条件を観察したり、自分が思いついた条件と実際の全パターンとの差分を列挙して改めて観察するということが手軽にできて、とても役に立ちます。
今回の問題では、文字列長ごとの数え上げを出力してみるだけでも良い性質が見えてきますね。おおよそ $3^N/4$ となっていて、確率 1/4 程度で生成可能パターンになるらしいというヒントがあります。$1/4$ で条件を満たすということで、$4$ 値あるいは $2$ 値の不変量を考えるという発想にはなると思います。偶奇性というキーワードを想起するのもそれほど難しくなく、不変量: $A+B$, $A+C$, $B+C$ の個数の偶奇が見つかります(公式解説では、$1,2,3$ に置き換えたときの xor を見ていますが、これらの偶奇の不変量に注目するのと完全に同じことです)。あるいは「個数に注目して何かないかなあ」と思い至ったのであれば、生成したパターンに対する個数の内訳の種類を全部列挙して観察してみたりするのも良さそうです。すぐに正しい解法に乗れなくても、試行錯誤できることはたくさんありますね。
$A+B, A+C, B+C$ の偶奇の不変量から、必要条件が出てきますが、今回の問題では十分条件とは少し差があって、同じ文字が奇数個並ぶ場合がコーナーケースとなります。このようなケースも全生成したものとの比較により簡単見つかり、言い換えに確証を持って次のステップに進むことができます。
なおこの手の言い換えでは、正しい主張を見つけるまでは大変ですが、見つけてしまえば証明は易しいです(帰納法など)。
次は、文字列 vs 文字列の判定問題を考えるという手順になります。特に操作手順に自由度があるので、「何らかの操作手順で作れるならば、こういう種類の操作手順でも作れる」のように操作手順を限定する(できれば文字列に対して一意化する)のが典型手法という感じです。
ここから先は発想力というよりは、やるべきことは大体分かるのを細部を整理しきる実力という感じだと思います。与えられた文字列に対する判定を行うには、なるべく貪欲に作っていくのが良さそうという気持ちには比較的簡単になると思うので、貪欲に作って判定できないのはどのような場合かを丁寧に場合分けして議論することになります。
(あとは大体公式解説と同じだと思うので、略)。
問題F – Esoswap
きっと常に出来るんだろうなとは思ったんですが、1 分考えて全く確証が持てなかったため。
この提出をして AC となるケースがひとつもない場合、ジャッジ対象はすべて構築可能ですね。提出から情報を得るテク。
考察の上では、以下の問題での経験が役に立ったと思います。(そんなに似ていないかもしれませんが、「たくさんあるルールをうまく利用しきるのは難しそうなので、扱いやすそうないくつかのルールに注目して構築してしまおう」という着想は、この問題での学びのひとつでした)

公式解説と違うアルゴリズム($O(N^2)$ ステップ)でしたので、書きます。(公式解説の方法、おもしろくてびっくり)。
「1」の挙動が分かりやすいです。
- 「1」は単体で好きな場所に移動可能。よって他の数の位置関係を正しくすればよい。
- 「1」をぐるぐる回していけば、全体をシフトできる。よって、左端がどこかなどは意識しないでよい(円順列と思えばよい)
などは読み取れます。$1$ は好きな場所に抜き差しできるイメージを持ったので、以後はその他:$0, 2, 3, \ldots, n-1$ の位置関係のみに注目します。
「$n-1$」も同様に分かりやすいので、まずは「$1, n-1$」の $2$ 種の操作を考えましたが、他の数の相対的な位置関係が不動のまま。そこで次に「$2$」を考えました。「$2$」だけ乱発しても制御しきれなさそうなので、「$1$」による位置調整と合わせて行えるシンプルな操作を考えます。
- $1, 2, x → 2, 1, x → x, 1, 2$
- $2, x, y → y, x, 2$
前者から、「$1$, $2$」ともに好きな場所に運べることが分かり、後者と合わせると $1,2$ 以外の数の相対的な位置関係を隣接互換できることが分かります。よってソート可能です。あとは動作の例を載せておきます。

$1,2$ の移動は「他の数の相対的な位置関係」を保つだけで、絶対的な位置は変わりまくるので、「転倒」の定義には注意が必要です。「$0$」を左端と見なしたときの位置を基準に定義して実装しました。
転倒をひとつ解消するのに最悪 $\Theta(N)$ ステップかかる(定数倍で数倍つく)ため、最悪ステップ数 $\Theta(N^3)$ だと思ってこの解法では AC が難しいかと一度は思いました(10 分ほど手が止まったところ)。しかし実際には、$[1,2]$ が配列全体を $O(N)$ 周すると全ての転倒が解消され、全体で最悪 $\Theta(N^2)$ ステップで済むようです。
アルゴリズムは、($[1,2]$ をループ変数と見なして、適当に文字を置き換えたりすると)おおよそ次のように進行します。
i = 0
while i < N:
if A[i] < A[i+1]:
i += 1
else:
A[i], A[i+1] = A[i+1], A[i]
i += 2 # ここが i+1 だったらバブルソートと同様スワップする瞬間にループ変数が $2$ つ進んでしまうことを除けばバブルソートと同様です。本番は、バブルソートとかなり似ているし、ループ変数が一周する間に転倒を $\Theta(N)$ だけ解消することが可能なアルゴリズムなので、$O(N)$ 周したがって $O(N^2)$ ステップでソートが終了すると判断し、実際に AC を得ました。
ただこれ、結構ちゃんと解析して証明するの、難しいですね。以下、考えた証明の方針です。
- 最小値($0$ とします)は、$2$ 周に $1$ 回は左に移動できる。$2k$ 周すれば位置 $\max{0, N – k}$ 以下に居ることが証明できる。
- 最小値から $2$ 番目($1$ とします)は、一度 $0$ よりも $2$ つ以上右側に来てしまいさえすれば、やはり $2$ 周に $1$ 回は左に移動できる。はじめて $0$ の右側に来る時刻・場所で場合分けして計算する。$2k$ 周すれば、位置 $\max{1, N-k+1}$ 以下に居ることが証明できる。
- 最小値から $3$ 番目は…
$2N$ 周でのソート完了が保証できそうですが、細部の計算は詰めていないので、定数倍くらい修正する必要はあるかもしれません。
