| A | B | C | D | E | F | |
| 問題文 | ■ | ■ | ■ | ■ | ■ | ■ |
| 自分の提出 | ■ | ■ | ■ | ■ | ■ | |
| 結果 | AC | AC | AC | AC | AC |
問題 F:コンテスト後 AC → https://atcoder.jp/contests/arc105/submissions/17355625
全体感想
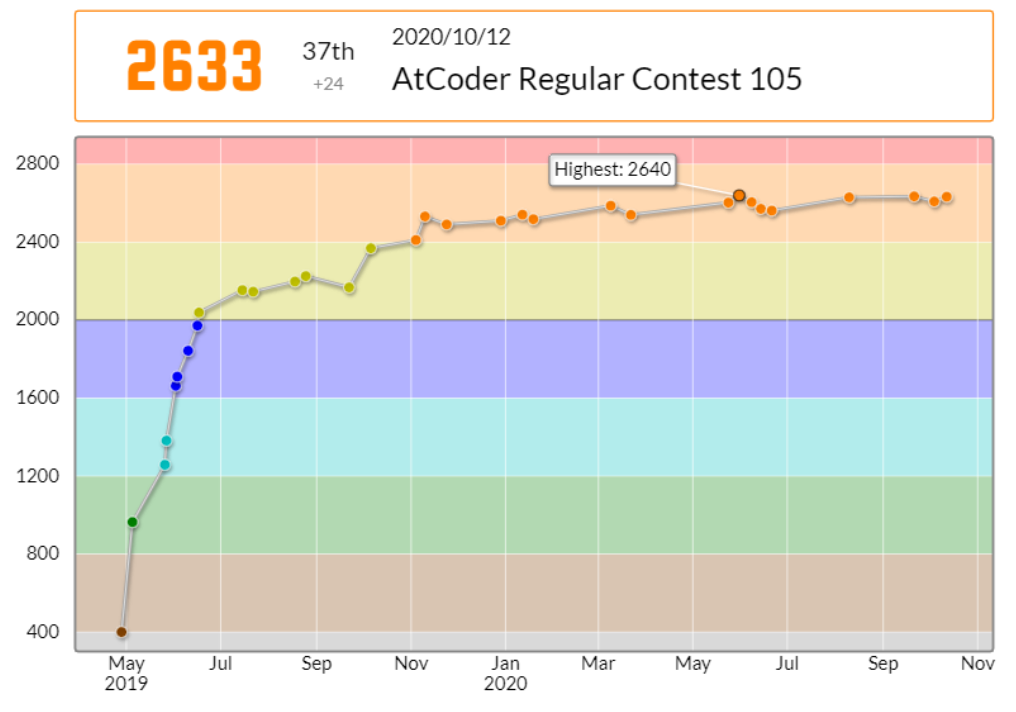
90分、ABCED の 5 完で、44位でした。
問題 F がそこそこ速く解ける回だったのに、時間を残せなかった・F を先に考える判断ができなかったため解ききれず、悔しいところです(Problems では銅 diff 評価ですが、100 分 6 問という要求速度の速さをかなり受けていると思います)。
問題 F は、好きそうな分野だったり AC が早めに出ていたら丁寧に読むつもりでしたが、グラフだったのであまりしっかり読まず。実際には線形代数や集合包除に近く、私の苦手なグラフ要素は少なめだったので、もっとしっかり読むべきでした。
結局、あと 30 分あれば解けたかどうか。くらいっぽいです。
ABCE のあと F に着手していた場合、ちょうど境界線上。これはこれで上手くいっていた保証はないですし、まぁ結果的にレーティング期待値は近かったかもしれません。仕方ないですね。
5 完 90 分は失敗寄りだとは感じなかったんですけど、やっぱり強い人は安定して高速で、まだまだ及んでいないと思わされます。
問題B – MAX-=min
テストケースが弱くて、シミュレーションで通るという解法も通るようです。
($A = [1, 1000000000]$ で既にシミュレーションがわりと厳しい。
同じところからの減算をまとめても、$A = [2, 999999999, 1000000000]$ で厳しい)
自明に見えましたが、一応脳内で数回証明を考えてから提出しました。まぁいいでしょう。
(ABC 以外では、序盤の問題を自明と思い過ぎて、誤読して間違えるパターンが複数回あったので、反省リストに入れています)
- 操作の最後に残る数を $x$
- $d = \gcd(a_1,\ldots,a_N)$
とします。まず、操作の過程で現れる数は、常にすべて $d$ の倍数であることが証明できます。したがって、$x$ は $d$ の倍数です。
また、操作を逆に遡ることで、操作の過程で現れる数は、常にすべて $x$ の倍数であることが証明できます。
Euclid の互除法で最大公約数が求まる理由を理解していれば、同様に証明できると思います。
問題D – Let’s Play Nim
苦戦、勝利条件を逆にして考察してしまってタイムロスしたのも大きかったです。
結構難しかったのに、AC 人数が多かったように感じてびっくりしていました。(すべては証明していないという提出も、一定数あるかもしれません)
Nim パートは有名問題です。それを除くと、$N$ の偶奇に応じて、次の 2 つのゲームを考えることになります。
- $N$ が偶数のとき:先手から始めて偶数回、山に石を置く。全体の $\xor$ が $0$ になったら先手の負け。
- $N$ が奇数のとき:先手から始めて奇数回、山に石を置く。全体の $\xor$ が $0$ になったら先手の勝ち。
さまざまな $\xor$ の中でぴったり $0$ を目指す必要がある側($N$ が偶数のときの後手、$N$ が奇数のときの先手)が厳しそうな勝利条件です。
勝てるときあるのかなあ?と考えていきます。
- $N = 2$ を考えると、$2$ 数が等しいときに後手が勝てると分かります。
- $N = 3$ のときに先手が勝てる気がしません。試しに、$3$ つの数が $10$ 以下のときに全探索解法を実装した結果、先手は全く勝てないという予想に至りました。
- $N = 3$ のときの証明を考えます。後手は、$1$ つの山を巨大にすることで、先手負けが確定します。
ここまでかなり発想の少ない考察だと思いますが、これで解答に必要な考察の種はすべてそろっていました。
$N = 4$ で、$[1,1,1,1]$ を考えると、後手が「オウム返し」で勝てることがわかります。これを一般化すると、$2$ 数ずつ等しいもののペアにできる場合に後手勝ちが予想できます。実際、$A = [a,a,b,b,c,c,d,d,e,e]$ などでゲームを進行してみると、容易に確認できるでしょう。(ちゃんと証明を書きたいのであれば、後手番の終了時に同一サイズの山のマッチングがある状態が維持できることを、帰納法で示せばよい)
あとは、それ以外の場合ですが、これは $N=3$ のときに考えた戦略(巨大な山を作ることにより勝ちを確定させる)がそのまま一般化できて、証明が終わります。
問題E – Keep Graph Disconnected
「連結成分のマージで、奇成分の個数は、$\pm 0$ または $-2$ で変化する」っていうの、グラフ理論で勉強した Tutte の定理のおもしろポイントだと思って記憶に残っていました。グラフ理論勉強会は競プロの役に立つ、かなー。
完全に公式解説通りです。とりあえず、ゲームの終了状態について考えると、$2$ つの連結成分の大きさの偶奇が問題だと分かります。($N$ が奇数なら運命は確定している)
あとは、常に奇成分が偶数個であることを念頭に置いて考察しました。成分が $3$ つの場合からしっかりと戦略を考えていけば、難しくはなかったです。問題 D より簡単?
問題F – Lights Out on Connected Graph
本番中にで解ききりたかったなー。完全にグラフ理論勉強会のおかげで思考がショートカットできたというやつ。まぁ終了後すぐに AC できて、取り組んできたことが(レートには結びついていないとはいえ)成果に現れているので、嬉しいです。今後とも、自分で考えた勉強法や練習法に自信を持っていきたい。
グラフ $G = (V, E)$ ($V$ は頂点全体、$E$ は辺全体)のカットとは、分割 $V = A\amalg B$ を用いて
$$E(A,B) = \{e=ab\in E\mid a\in A, b\in B\}$$
と書ける辺集合です。カット全体はそれっぽい加法により $\F_2$ ベクトル空間をなし、これを $G$ のカット空間といいます。
カット空間にはいくつかの記述があります(次元が簡単に記述できたり、基底が簡単に作れたりする)が、辺の生成する $\F_2$ ベクトル空間のうちで、$E(v) = E(v, V\setminus v)$ の形の辺集合が生成する部分空間がカット空間に一致することが知られています。
今回の問題ではいかにも、$E(v)$ の形で生成される $\F_2$ ベクトル空間が登場しているので、よいグラフの後者の条件が「$G$ の辺全体がカット空間に属する」と言い換え、さらによいグラフを「連結二部グラフ」と言い換えるまで、かなり一瞬でいけました。
そこから答を求めるところがまた、おおよその筋道は見えても思考の整理に時間がかかるやつです。「二部グラフ」のままだと、非連結なものを考えるときに、部集合への分割が $2$ 通りあってしっくりこなかったので、次のようにしました。
この手の数え上げでは、「簡単に計算できるものは何かを考える」こととか、「数え上げ対象の定義を明確に記述する」を意識しています。
- グラフ $G = (V, E)$ と分割 $V = A\amalg B$ の組 $(G,V,A,B)$ であって、$AA$ 辺、$BB$ 辺のないものを、ラベル付き二部グラフと呼ぶことにする。(ひとつのグラフが複数の方法でラベル付き二部グラフになりうる)
- 求めたいのは、頂点集合を $V$ とする $G$ の部分ラベル付き連結二部グラフの個数の、半分である。
- $\dp_1[S]$ を、$S\subset V$ を頂点集合する $G$ の部分ラベル付き二部グラフの個数
- $\dp_2[S]$ を、$S\subset V$ を頂点集合する $G$ の部分ラベル付き連結二部グラフの個数
以下、計算手順です。
- $\dp_1[S]$ を数え上げるには、全ての分割 $S = A\amalg B$ に対する和をとればよい。
- $(S, A, B)$ の個数は全体で $3^N$ 通り。
- 固定した $(S,A,B)$ の寄与は、$AB$ 辺の個数を $e$ とすると、$2^e$ 通りである。よって $e$ が計算できればよい。
- 両端点が集合 $S$ に属している辺の個数を $f(S)$ とすると、$e = f(S) – f(A) – f(B)$ である。したがって、すべての $f(S)$ を前計算しておくと、$\dp_1$ の計算は $\Theta(3^N)$ 時間で行える。
- $f(S)$ の前計算は、愚直にやれば $\Theta(N^22^N)$ 時間で行える($N2^N$ にもできる)
- $\dp_2[S]$ を数えたい。
- $\dp_1[S]$ を場合分けする。
- $v_0\in S$ をひとつとる。$v_0$ の連結成分で場合分けをする。
- $\dp_1[S] = \sum_{v_0\in T\subset S}\dp_2[T]\dp_1[S\setminus T]$ という式が得られる。
- 特に、$\dp_2[S] = \dp_1[S] – \sum_{v_0\in T\subsetneq S}\dp_2[T]\dp_1[S\setminus T]$ と計算できる。
- $(S, T)$ は $\Theta(3^N)$ 通りなので、ここも計算量 $\Theta(3^N)$。

