| A | B | C | D | E | F | |
| 問題文 | ■ | ■ | ■ | ■ | ■ | ■ |
| 自分の提出 | ■ | ■ | ■ | ■ | ||
| 結果 | AC | AC | AC | AC |
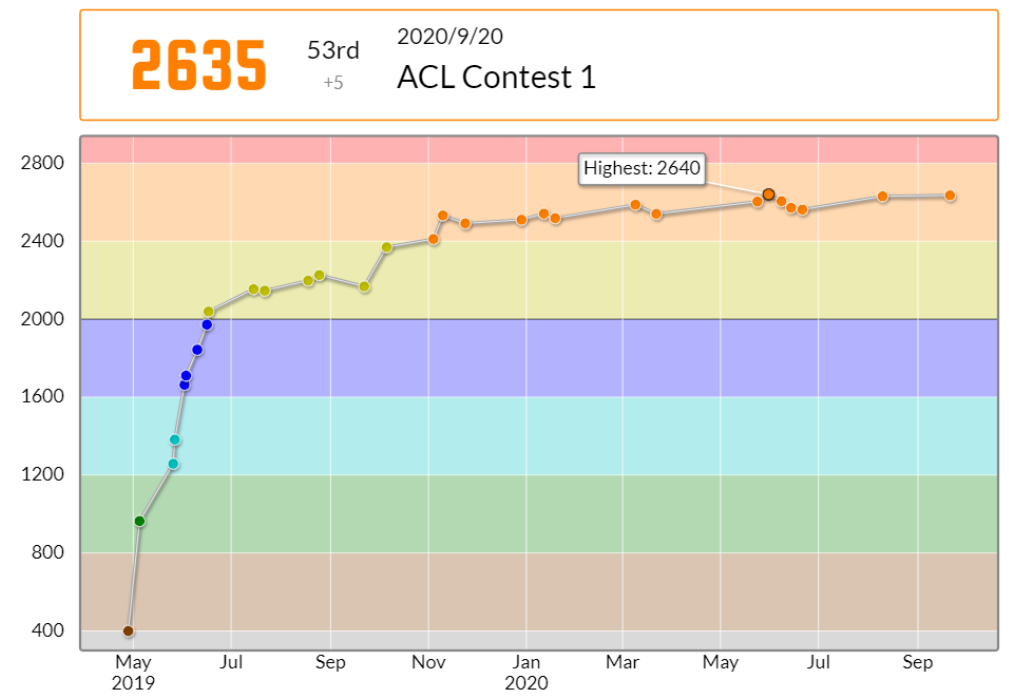
全体感想
133分、ABCE の 4完(3ペナ)で、53位でした。
解いた順番:B → E → C → A
と、なんか変わった順番に。解きました。
A:見る。10分で解いたつもりが、サンプル2 が合わない。誤読していたと発覚(1手で進める場所を数える別問題を解いていた)。すぐに解けず、一旦他を読むことに。
B:すぐに解ける。
C:操作順に依らず決まるかな?と思うも反例があることを確認。フローっぽいと思うも自信がないので後回し。(ACLだしというメタ読みもありました。)
D:ダブリングで最大個数がとれることはすぐに分かる。(https://yukicoder.me/problems/no/878 思い出した。)最大個数の計算を実装する(あまり問題を読んでいなくてひどい)。合わない。聞かれているものが割とヤバそう。ひとまず後回しでEを読む。
E:分かりやすそうな問題設定。5分くらいで方針が立って、そこから細部を詰め、20分くらいで実装を終える。サンプル 2 の答が合わない。手計算とプログラムの出す途中計算結果が一致することをひたすら確認。愚直シミュを書いて、実装も有理数に直して、答の比較。などと頑張る。流石におかしいと思い、読み直したら、mod の値が間違っていました($10^9+7$ を $998244353$ に直したら通るところに 40~50分かけてデバッグしていた)。
C に戻る。容量は非負だけどコストは負にして良いことを思い出し、最小費用流で解ける。
A に戻る。B, C, E と比べて易しいとは思わなかったが、流石に解ける。
残り 15 分。厳しい。(終了)
ちょっと誤読が多くてひどかったです。mod の勘違いでこんなに時間を溶かしたのは、本番では初めてです。
また、問題Aの誤読は、コンテスト 1 問目の難易度ならこんなもんだよねーという先入観も原因となっています。(AGC-A でも超自明問題と誤読したこと経験があって)。
mod 誤読がなくスムーズに進められたら D に 1 時間以上残せたはずで。その 1 時間があれば解ききれたかは正直分からないですが、くだらないところでパフォーマンスを大きく下げてしまいました。
失敗かなーと思った回のパフォが上がってきていると前向きに捉えつつ。
数か月前から、コンテスト直前に見直す注意事項とか思い出す考察パターンを書き出したものを作っているのですが、今回の失敗も追加して、今後の糧としたいと思います。
問題A – Reachable Towns
右上や左下に辺を張ったグラフにおいて、連結成分を数える問題です。そのままだと辺が多いので、要る辺にしぼることが問われています。
処理が $2$ 通りあると面倒なので、左下側から右上側に辺を張ることだけを考えました。特定の点からどこに辺を張ればよいかを考えて、しばらくあまり上手くいかず。
左の点から順に処理することを考えて、正答に行き着きました。
私の解法を説明します。点 $(1, y_1)$ から辺を張ることを考えます。右上領域は一気にまとめて連結成分になります。ここには $O(N)$ の点がありますが、ひとつずつ辺を張ってしまいます。その分、これらの点の処理を今後削減できないかを考えます。
まず、これらの点からは二度と右上方向の辺を張る必要がありません。また今後、この領域に向かって辺を張る際には、ひとつだけ張れればよいです(同じ連結成分であることが確定しているので)。
他の点からこの領域に、ひとつ以上辺が張れるかどうかの判定ができれば良いです。その際、$y$ 座標は関係なくなります。$x$ 座標についてだけ見て辺を張ればよいです。したがって、右上領域における最も右側の点以外は、今後存在しないものとして取り扱えます。
各時点で、
- 自身の右上領域で、残っている頂点すべてに辺を張る
- それらの頂点のうち、最も右側にある頂点以外は削除する
という処理を行っていけばよいです。
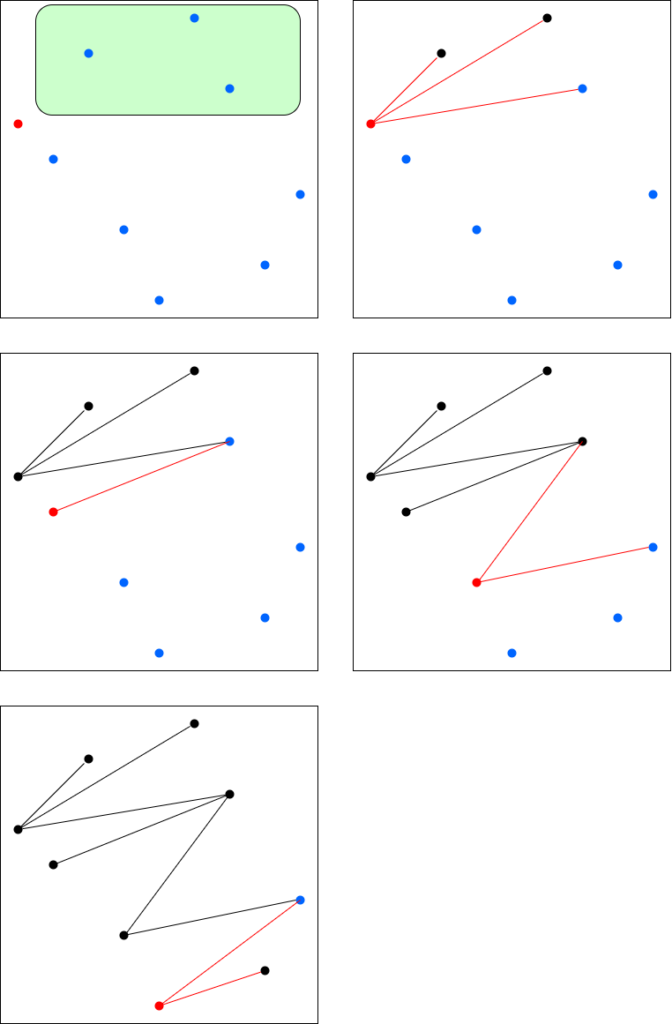
辺をたくさん張るとその分、今後見るべき頂点が減るため、辺を張る操作は償却 $O(N)$ 回しか行われず、あとはこれを適切に実装すれば解けます。
【翌日考えたこと】
連結成分は、$x$ 座標で見れば区間に分割されるのですねー。気づきませんでした。それまで探索した点の $y$ 座標の最小値も持って左側から探索すれば、どこで連結成分が完結する場所も分かります。$\Theta(N)$ 時間解法になりました。
提出:https://atcoder.jp/contests/acl1/submissions/16928237
1問目から、dsu と fenwick tree を想定解に取り入れている ACL 仕様でハイレベルだなと思いましたが、どちらも要らなかったようです。
問題B – Sum is Multiple
まぁまぁ整数論慣れはしているので、流石に一瞬で解けましたね。こういうのが苦手なら、Project Euler を解き進めるのも良いと思います。また、例えば $x^2\equiv x\pmod{10000}$ を解くなど高校数学でも見かけたことがあるような気がします。
$k^2 + k\equiv 0\pmod{2N}$ を解く問題です。素因数分解を $2N = \prod p_k^{e_k}$ とすると、これは $k^2 + k\equiv 0\pmod{p_k^{e_k}}, \forall k$ と同値です。
ひとつの $(p,e)$ に対して $k(k+1)\equiv 0\pmod{p_k^{e_k}}$ を考察すると、$k, k+1$ は互いに素でどちらかは $\pmod{p_k^{e_k}}$ での可逆元となることから、$k, k+1$ のどちらかが $0$ つまり $k\equiv 0, -1\pmod{p_k^{e_k}}$ と同値です。
素因数が $n$ 個あると、解が $2^n$ 個あることも分かります。これらを全て求めて、最小の解を答えればよいです。
$k\equiv -1\pmod{p_1^{e_1}}, k\equiv -1\pmod{p_1^{e_2}}$ といった条件同士はプログラミングによる計算をせずとも、すぐに $k\equiv -1\pmod{p_1^{e_1}p_2^{e_2}}$ とまとめられるので、CRT ライブラリは使わなかったです。結局 $ab=2N$ かつ互いに素な $(a,b)$ に対して、$k\equiv 0\pmod{a}$ かつ $k\equiv -1\pmod{b}$ を解けばよくて、$k = an$ と表すと $an\equiv -1\pmod{b}$ となるので、inv_mod ができればよいです。
Python なら、inv_mod は、組み込み関数 の pow を使って pow(a, -1, b) により計算できます。
問題C – Moving Pieces
ACL じゃないところで出ていたら、フローだと思うまでにもう少し時間がかかったかも。
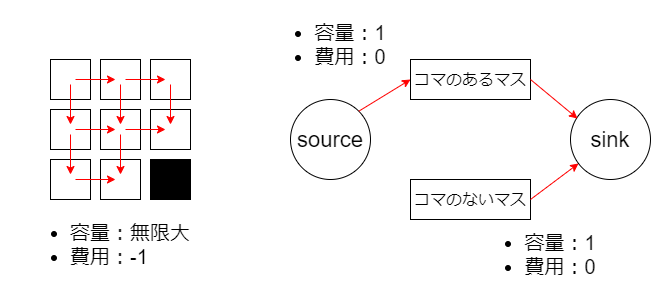
移動にコスト $1$ を充てると「最大費用流」みたいになっちゃってしばらく迷いました。
最小費用流はコスト負の辺があっても正しく定式化できるので、$-1$ にするだけでした。(辺の容量は正である必要があって、例えば問題を最小カットに書き直すときには気を遣いますが、それと混同していました、練度が低かったです。)
フローは水を流すこと、とも思えますが、この問題に関してはもっと定義通りに、「辺ごとに流量を定める」「各頂点で釣り合う」と思って取り組みました。
各頂点に向かってくる移動、出ていく移動の回数は「ほとんど」釣り合う必要があります。ずれとしては
- 始めからコマがあると、入ってくる回数が $1$ 少ない
- 最後にコマがあると、出ていく回数が $-1$ 少ない
となって、これらは source, sink との間の容量 $1$ の辺として定式化できます。始めにあるコマの位置は強制で、これは source から各コマに辺を張ったあと、全体の供給量をコマの数に設定すればよいです。
移動をフローで表せることは分かりますが、最小費用流をコマの移動として表せることも確認しておきます。まず、すべての容量と流量が整数であるような最小費用流問題には、整数流(任意の辺の流量が整数であるような解)が存在します。また、多くのアルゴリズムは実際に整数流を返すように設計されています。よって、各頂点に、整合性のとれた各方向の移動回数を定めることができます。
実際にその回数に従った移動が、コマの衝突なしに実現できることを確認します。DAGなので、フローに閉路はできていません。よってフローはパス分解を持ち、それにしたがってひとつひとつのコマの移動経路を定めていきます。経路を定めたら、コマが衝突しそうなときには後ろのコマを先に移動するように修正していけば、コマの移動を順にひとつずつ定めることができます。
Python であれば、ACL を移植せずとも networkx で最小費用流アルゴリズムを利用できて、手軽な選択肢となると思います。ノードは整数である必要はなくて、ハッシュ可能なオブジェクト(タプル $(i,j)$ や ‘source’ 等の文字列など)が使えますから、頂点をエンコードする方法などを考える必要がないです。(その分、パフォーマンスはいまいちです)。また、単一の source、sinkを指定する形ではなく、複数の需要・供給点を指定する形になっています。
問題D – Keep Distances
本番中はほとんど考察できませんでしたが、コンテスト後に解きました。
極大な集合は、貪欲に取っていけばよくて、ダブリングの前計算で求められます。これはかなり典型だと思います。(例:PAST202004-M)
- 各頂点から $2^k$ 回進むときの移動先を、$k=0,1,2,\ldots$ 順に求める。
- $2^{k}$ 回進むことは、$2^{k-1}$ 回進むこと $2$ 回なので、全体で $\Theta(N\log N)$ での前計算ができる。
- クエリには、大きな $k$ から順に、$2^k$ ステップ進めるかどうかを計算していくことで、$\Theta(\log N)$ で答える。
聞かれているもの(和集合)が厄介です。必要なデータ構造等を考えるより先に、これの良い計算方法を手に入れないといけません。
すべてのありうる集合を列挙するのはつらいです。コンテスト中は、短時間ですが、各要素 $X_i$ を含むものの存在判定をする方法を考えました。これだと計算量が減りません。
和集合の大きさを計算する場合分けの軸として、左右への移動回数を使います。すると、求める和集合は、区間に分割されて、良さそうな構造が見えてきます。$X = [1,2,…,105], K = 10$ みたいな観察すると、見えやすいです。
これに気づけばあとは簡単です。区間の右端になる座標の和と、左端になる座標の和を計算できればよくて、これらは両端からの貪欲で求められるので、ダブリングの前計算で座標の和も求めておくだけです。
左右からの前計算 2 つを求めないといけないので、このロジックをまとめて実装すると簡潔に実装できると思います。私は右からの計算は、$[-x_n, -x_{n-1}, …, -x_1]$ に対する左からの計算としてロジックをまとめました。
問題E – Shuffle Window
これは割と一直線に考察できました。
まず、各々の $2$ 個組の、寄与を分析します。その際、ある $2$ 数が一度でも同じシャッフルに巻き込まれると、その $2$ 数の転倒数の条件付き期待値は $\frac12$ になります。
このことに気づくと、あとは比較的易しいです。
もともと $A[i], A[j] (i < j)$ の位置にあった $2$ 数に対する転倒数期待値を考えます。これは、$A[j]$ がシャッフルされ始める時点での、$A[i]$ の生存確率(シャッフルで左端に一度もならない)と等しいです。
あとは、この $O(N^2)$ 組の計算をまとめます。$j$ ごとに $i$ に対する計算をまとめて行うことを考えます。
$A[i] < A[j]$ であるか否かごとに、生存確率の総和したがって、各 $A[i]$ の生存確率を管理しつつ、そのような $i$ も取得できるようにします。キーを $A[i]$ の値とした適当なデータ構造で区間ごとの総和を取り出せるようにすればよいです。
生存確率は、毎回一様に $p$ 倍される形になりますが、区間作用のできるセグメント木を用いてもよいですし、取り出してから $p^j$ をかける形にすれば区間和だけでよい(その分だけ、挿入時に調整します) ので、区間作用のないセグメント木あるいは Fenwick Tree で管理すればよいです。

