| A | B | C | D | E | F | |
| 問題文 | ■ | ■ | ■ | ■ | ■ | ■ |
| 自分の提出 | ■ | ■ | ■ | ■ | ■ | ■ |
| 結果 | AC | AC | AC | AC | AC | AC |
全体感想
ABC-rated の企業コンテスト。

・問題F:First AC
・総合順位:2位
ということで、とても良い感じの出来でした。良い結果が出たので確認したところ、賞金はないようです(笑)
ABC-rated とはいえ、企業コンテストの方がすこし難易度が高めなのでしょうか?パナソニックのときも少し難易度高めでした。
今回のセットも、問題D, E がいつもより難しくて苦戦させられました。
問題A – Number of Multiples
O(1) 解法:https://atcoder.jp/contests/aising2020/submissions/15174257
問題D – Anything Goes to Zero
まず、クエリなしの場合に考えます。はじめの 1 回の計算で、
・popcount(X) を計算する。これは N 以下になる。
・X を popcount(X) で除算する。N 以下になる。
となります。このように、今回の操作は、たった 1 回計算するだけでめちゃくちゃ値が小さくなります($2$ 進法 $200000$ 桁から、$N$ 以下($2$ 進法 $18$ 桁)になる)。
$N$ は一見巨大ですが、操作による減衰がめちゃくちゃ早くて、一回の操作あたりの計算が十分高速でありさえすれば、操作列を実際にたどって $f$ を計算しても十分高速であることが期待できます。
$2$ 回目以降の操作は $2$ 進法 $18$ 桁程度ですから、$1$ 回目の操作に $\Omega(N)$ かけないようにだけ気を付ければよいです。あとは、mod をとる値(popcount(X_i))が $2$ 種類しかないことと、$X$ と $X_i$ の差分は容易に計算できることに注目すればOKです。
$X_i = 0$ となる場合の回避も微妙で、問題 D にしては気を遣う問題でした。
問題E – Camel Train
はじめ、フローを考えました。「ラクダと日付の最大マッチングで、コスト最大のものを求めよ」ですから、たとえば最小費用流で解けそうです。これだと間に合わないので、(ラクダ, 日付) に対するコストが綺麗な規則になっていることを利用していかないといけません。
とりあえず、$(L, R)$ と $2$ 値がありますが、「必ず $R$ 点得る。左側のときにおまけで $L-R$ 点得る」ような形にして、基礎点と追加点を分けて考えることで、パラメータをひとつ減らすことができます。
・「全員、左側に追加点が定義されていて、正負の混ざっている」
・「全員、非負の追加点が定義されていて、左右が混ざっている」
のどちらにしようかかなり迷って、しばらく試行錯誤していました。結果的には後者が良かったです。この手の割り当て問題では、コストの符号をそろえておくことが多くて…フローだと思っていたりした以上、符号をそろえるのが典型的な考え方でしたかね。
・左を希望するラクダの、(締切、追加点)
・右を希望するラクダの、(締切、追加点)
が定義されていて、追加点をたくさん得ようという問題です。左右独立に考えられれば簡単に解けそうですが、独立に解くだけでは、右側で希望を通したラクダと左側で希望を通したラクダが衝突すると困って………。
ここで 10 分以上悩んでいましたが、衝突するわけがありませんでした(笑)
$N$ マスあって、左端・右端から使っていって、合計 $N$ マス未満しか使わないので。
左右独立に解けばよいです。ちゃんと ABC コンテストを全部履修していれば解けるでしょう。

問題F – Two Snuke
参考:
まず、問題を形式的べき級数で表しましょう。
$$ f = \sum_{0\leq s1 < s2} (s_2 – s_1)x^{s_1 + s_2}$$
とします。$\sum_{n=0}^N [x^n] f^5$ を求める問題だと分かります。係数の累積和をとる操作は、$(1-x)$ で割る操作と対応しますから、$[x^N] \frac{f^5}{1-x}$ を求める問題だと分かります。
よって、あとは $f$ がいい感じに求まれば良いです。単純に $s_1, s_2$ をループして計算してみます。
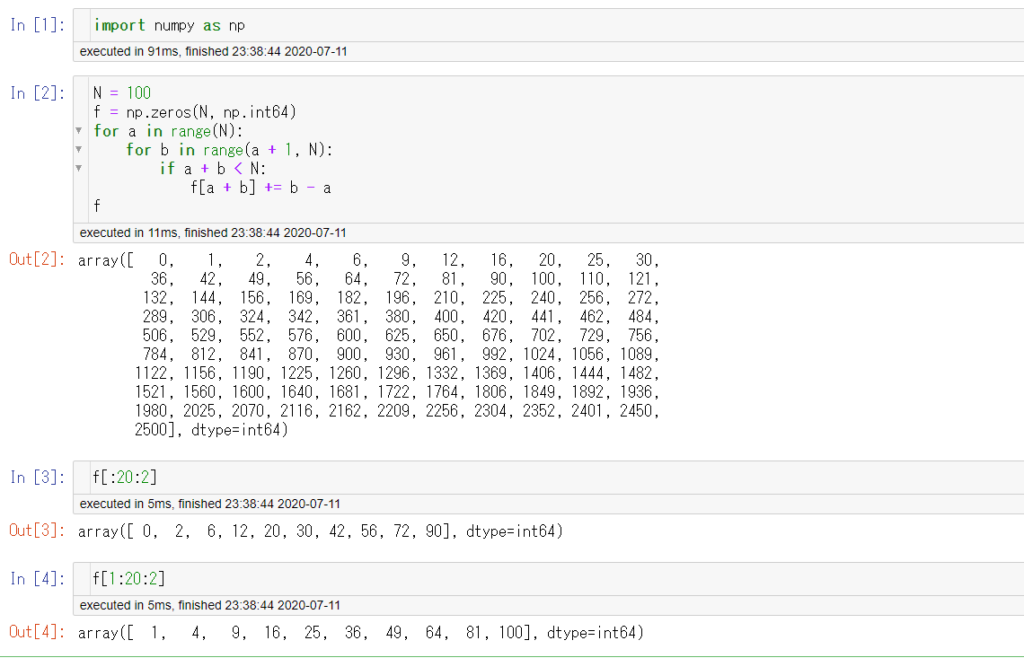
奇数次、偶数次のところで $2$ 次多項式の規則になっています。この時点で、$f = \frac{P}{(1-x^2)^3}$ と書けることは確定します。有理式で書けるような形式的べき級数については、
などを参照してください。「$2$ つおきに見て $2$ 次式」ですが、これが単に「係数が $2$ 次多項式」であれば、分母 $(1-x)^3$ を持つ多項式です。$2$ つおきなので、$(1-x^2)^3$ とします。
実際にはもうちょっと小さな分母でよいです。$(1-x)$, $(1+x)$ を適当に掛け算して、多項式になる待ちをします。

$(1-x)^2$ を $2$ 回掛け算すると、$\frac{x}{1-x^2}$ になったことが確認できました。
コンテスト本番も、こうやって、掛け算した形式的べき級数を表示する実験を手早く回していました。
$f = \frac{x}{(1-x)^3(1+x)}$ が得られたので、問題の解は、$5$ 乗したあと $(1-x)$ でわって、$$[x^N] \frac{x^5}{(1-x)^{16}(1+x)^5}$$ を答えればよいです。
あとはこれを、Fiduccia’s algorithm などで計算すればOKです。私は、Ryuhei_Mori(https://twitter.com/Ryuhei_Mori?s=20) さんの記事http://q.c.titech.ac.jp/docs/progs/polynomial_division.html を参考にライブラリ化しています。
この方法は、$N$ について $\Theta(\log N)$ の計算量となりますが、
で取り上げた方法で、クエリ $O(1)$ で解くこともできます。求める値はある多項式 $P$ によって $$[x^N] \frac{P}{(1-x^2)^{16}}$$ と書けるので、偶数番号、奇数番号それぞれで見ると $15$ 次多項式の規則となっており、$16$ 項ずつ計算しておけばあとは多項式補間で解くことができます。

