| A | B | C | D | E | F | |
| 問題文 | ■ | ■ | ■ | ■ | ■ | ■ |
| 自分の提出 | ■ | ■ | ■ | |||
| 結果 | AC | AC | AC |
全体感想
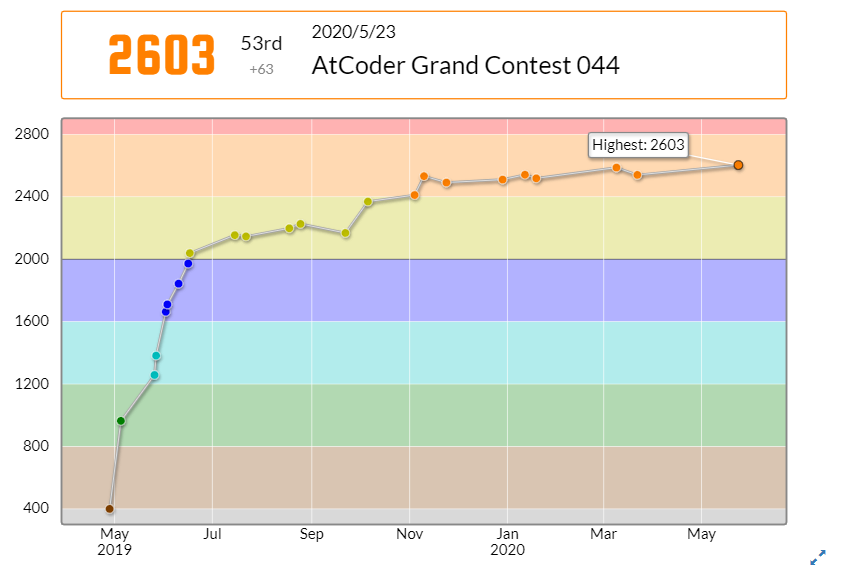
久しぶりの Rated!
レーティングが変動するのもうれしいですが、ARC, AGC は問題の質も高いと言われているとおり、ABC コンテストに比べて解きごたえがあって、嬉しいです。
97分3完で、53位でした。
前回、高難度帯を優先して破滅してしまったので、今回は、解けるレベルのものはきちんと解いて、期待値よりも最低値を底上げしようという意識でした。
C までしか解けませんでしたが、ABC はどれも面白い問題でした。
Eが、ひねりの少ないストレートな高難易度に見え、こういうの解けるようにしていきたいなー。$\Theta(N^2) $ 解にはなったのですが、そこから進展せず。
Dも並行して考えていたのですが上手くいかず(実は割と良いアイデアは出ていたみたいですが育てられず)でした。
2 度目の赤パフォで、レーティングは Highest を更新しました。Rated が続くので引き続きがんばります。
問題A – Pay to Win
とりあえず、掛け算を遡って小さい数にすることは考えます。
最後に行った掛け算がどの種類であるかを固定してみます。例えば、$N=11$ として、最後に行った掛け算が $2$ 倍であるとします。
逆順にさかのぼって、「$11$ → $10$ → $5$」「$11$ → $12$ → $6$」という操作列はぱっと浮かぶと思います。
これ以外にないかを検証します。例えば「$11$ → $8$ → $4$」のように、3つ引いてから $2$ で割るようなパターンです。上に取り上げた操作と比べると、「$11$ → $10$ → $5$ → $4$」と操作することの完全下位互換になっていることから、このような操作は考える必要がありません。
結局、上下の直近の $2, 3, 5$ の倍数まで移動してから割り算で移動するような遷移しか考える必要がないことが分かります。(例えば 5 で割るときに、$5k+3$ からは $5k + 5$ だけ見れば良いことなども分かりますが、計算量にはあまり関係ないです)。
あとはこれを詰めてメモ化再帰にして計算量解析すれば終わりです。
・実装
ありうる場合を漏れなく場合分けしましょう。「最後に行った掛け算が $2$, $3$, $5$ 倍」に相当するのが上述の議論です。これに「$1$ 度も掛け算を行わなかった場合」も含めてあげればOKです。再帰なので、終了条件にも気を付けます。実装によっては $N=1$ あたりで無限ループになりかねないので気を付けましょう。
・計算量解析
遷移で登場する数は、$\frac{N}{2^x3^y5^z}$ の形の整数あるいはそれに $1$ 加えたものしかありません。私の「桁dp」の理解の仕方(ABC138-F, ABC154-E など)だと、分母が単一のときにいつもやっている考え方なので、すぐに反応できました。$2^x3^y5^z \leqq N$ となる $x,y,z$ は $\Theta(\log N)^3$ 通りで、これが計算量となります。
問題B – Joker
問題文ちょっと笑っちゃいますよね(永遠に~)。
人の居る場所を通るとコスト $1$ かかるとして、各時点での、外周までの最短距離を求めたいという問題です。
結構、ダメ方針も考えました。何らかの意味で連結成分の計算をまとめようとしたり、逆再生を考えたり。人の増減で計算対象の値が変化するところの根本的な問題が解消しません。
全マスから外周への距離を持って、順次更新していくことを考えてみます。ひとり離席した影響を受けるマス目だけを更新対象とすれば、いくらか計算が抑えられそうです。あるマス目が更新されたら、その $4$ 方向を候補とする基本的な bfs or dfs ですね。
より詳細には、人の居るマス目の通過コストを $1$ として、各マス目に対して、「外周までの最小移動コスト(ただしそのマス自身のコストも含む)」を持たせました。(自身を含むかどうかは、概念定義を明確にしておきさえすればどちらでもよいと思います。)
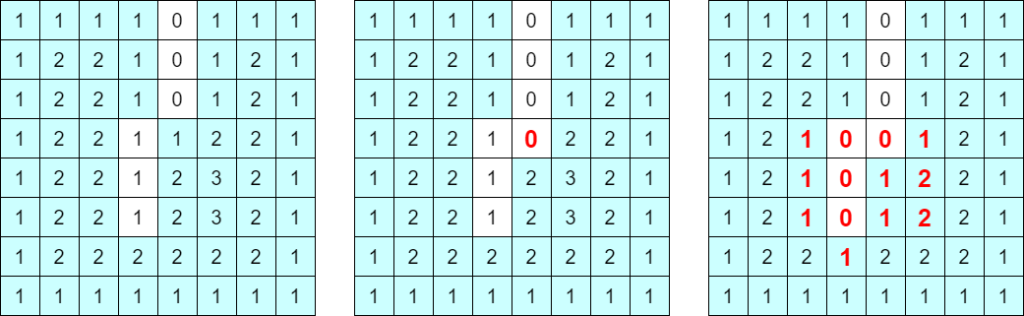
1 人席を立ったときの更新です。検証すべきマス目が少なくなったので、例えば毎回 bfs する等よりは計算量が良くなっている気がします。
$1$ 人離席ごとの計算量では、更新対象となるマス目の個数が $O(N^2)$ でしか評価できず、全部足し合わせて $O(N^4)$ というのがひとつの評価です。もう少し頑張ります。
全過程を通した計算量(償却計算量)を解析する際には、操作の回数に合わせて減少する量(より一般にはポテンシャル)に注目するとよいです。$1$ 人の離席に注目するのではなく、bfs / dfs での探索 $1$ 回に紐づく減少量を考えようとすると、探索 $1$ 回あたり必ず外周までの距離の総和が減少量になることが分かります。
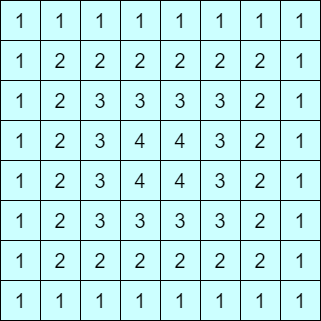
例えば $N=8$ であれば、距離の更新回数は、上の数の和でおさえられます。この数の和は、$8^2 + 6^2 + 4^2 + 2^2$ に等しいです。$N=500$ だと、$500^2+498^2+\cdots+2^2$ です。だいたい $\frac16\cdot 500^3$ 程度なので、$2$ 秒制限で十分解けます($\sum_{i=1}^N i^k$ の形の計算量、係数に小さな定数倍がつきがち)。
問題C – Strange Dance
AGC-Cの中でもかなり好き寄り~。
とりあえずサンプルを全て手計算であわせます。流石に、「SS」は消せる(例えばサンプル $2$ は、「RRSRR」と同じ)ことはすぐに分かります。
例えば、$N=3$ のとき、$[0,9)$ 部分は $N=2$ のときとサルサの挙動が同じだなーとか思います。$N$ がとても大きいと、ここの境界を出入りしない人は同じ構造だなーなどと。言い換えると、$3$ 進法表記の一番上の位を見ています。$1$番上の桁は、たまに繰り上がって入れ替わる以外は分かりやすい挙動なので、入れ替わる部分だけ上手く処理する?みたいな(結果的にはこうは解かなかったが、着想の種にはなったと思う)。
次に、一番下の位も追ってみます。何とびっくり、というか当たり前ですが、$\pmod{3}$ での値を固定すると、ダンス終了時の $\pmod{3}$ の値も定まることが分かります。これは綺麗な構造なので、何とかこれを利用できないかと思いました。
例えば、サンプル 2 を見ます。$1$ の位が $2$ の人は、$1$ の位だけを見ると、
$$2 \stackrel{R}{\longrightarrow }0\stackrel{R}{\longrightarrow} 1 \stackrel{S}{\longrightarrow}2\stackrel{R}{\longrightarrow}0\stackrel{R}{\longrightarrow}1$$
と変化します。この方々の、終了状態における $1$ の位は $1$ だということです。
さらに、この方々の $3$ の位はどうなるかを考えると…。良い感じに再帰的な構造が現れました!
「S」は当然、$3$ の位より上だけを見ても、桁ごとの $1$ と $2$ の入れ替えです。「R」の、$3$ の位より上へのふるまいは、繰り上がりの有無によって $+0$ または $+1$ です。なのですが、$1$ の位が固定された方々だけを対象とするのであれば、繰り上がりの位置は固定されています。つまり、
- $\stackrel{S}{\longrightarrow}$:上位の位についても「S」として振る舞う。
- $0\stackrel{R}{\longrightarrow} 1$:上位の位では無視される。
- $1\stackrel{R}{\longrightarrow} 2$:上位の位では無視される。
- $2\stackrel{R}{\longrightarrow} 0$:上位の位では「R」に相当。
といった具合です。
よって、サンプル 2 は、
- $1$ の位が $2$ の場合の遷移を考える。移り先の $1$ の位が $1$ であることと、上位の位が $T=RSR$ の問題と見なせることが分かる。
- $N=1$ かつ $T=RSR$ の場合を解く:$0\to 0$, $1\to 2$, $2\to 1$.
- したがって、$02\to 01$, $12\to 21$, $22\to 11$ と求まった。
- 答の「$-,-,1,-,-,7,-,-,4$」の部分が求まった。
というように、小問題を $3$ つ解く再帰により計算できることが分かります。
あとは、計算量解析をしてコードに落とせばよいです。雑には、繰り上がらない $R$ が無視できることから、$R$ の個数が $1/3$ ずつになっていくと見てあげればよいです。$S$ の個数が減らないと困りそうですが、「$SS$ は捨てられる」ことを思い出すと(サンプル 2 が親切)、文字列長は $R$ の個数の $2$ 倍くらいで上から評価できるので、$R$ の個数だけを追っておけばよいでしょう。
真面目にやると、再帰先の $R$ の個数の和が再帰呼び出し元と同じです。したがって、再帰の深さと合わせて、計算量 $\Theta(3^N+N |T|)$ が分かります。

