
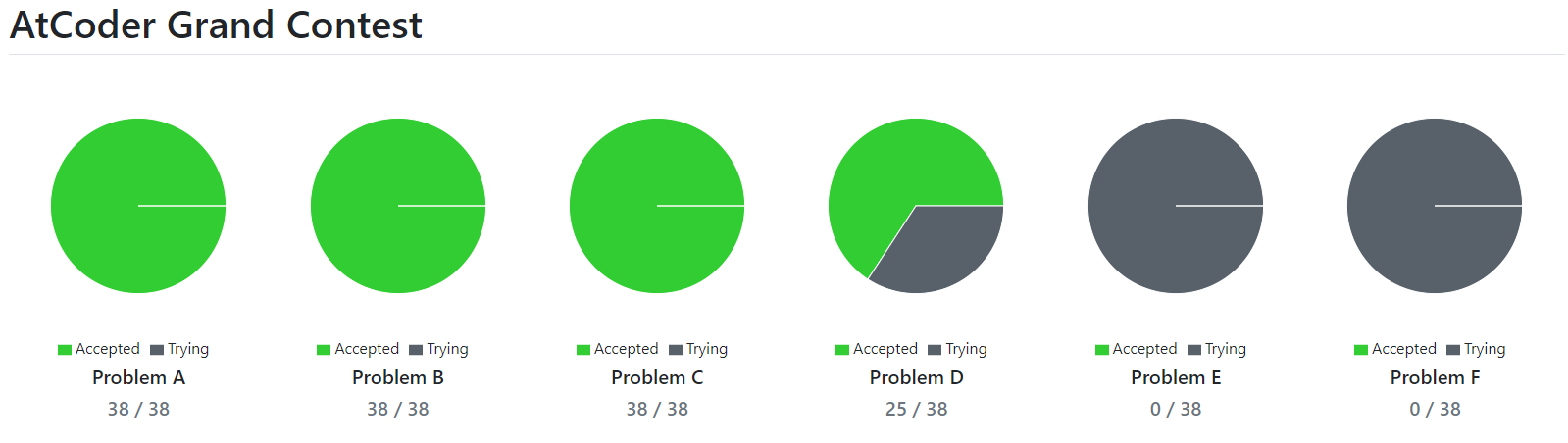
| A | B | C | D | E | F | |
| 問題文 | ■ | ■ | ■ | ■ | ■ | ■ |
| 自分の提出 | ■ | ■ | ■ | ■ | ||
| 結果 | AC | AC | AC | AC |
全体感想
95分4完で、24位でした。
・AGC4完 → 過去最高!
・AGC24位 → 過去最高!
・パフォーマンス値3283 → 過去最高!
・Rating 2369 → 過去最高!
となって、大当たり回でした。
とりあえず6問とも見る。A,Dがすぐ解けそうな気になる。そのうちAは微妙に細かい実装で気をつかいそうなので、Dを真っ先に倒しました(Fastest ACまであと1分、惜しい)。
Dは数オリ数学である程度代表的…なだけでなく、特に、有名本にあるので、まぁ得をさせてもらいました。数オリ数学といっても、知識として標準装備しているのが数オリやり込み勢くらいかなというだけで、標準的な中高数学で自然に考察できる範囲です。割と賛否(好き嫌い)もあったようですが、そもそも普通に中学幾何か座標で高校数学の計算頑張ればよい範囲ですし、知識ゲーとして片づけてしまうのも少し違うとは思います。まぁ数学背景知識があると得できたのは間違いない。
「数学の知識、考察がとても強ければ、アルゴリズムと実装に強いだけの人を上回れる」という場面は過去問でも珍しくなく。atcoderが、単純なプログラミング能力だけでなく、プログラミングをツールとした数学寄りな問題の解決能力を評価していることは今更いうまでもないこと。そうなると、「atcoder上位と比べても数学の知識・考察を武器にできるレベルに数学が強い人」がたまに得しちゃうのはそりゃそうで。私としては、今後もそういうところの恩恵を受けられるようにしていきたい所存。
という感じでDのおかげで高評価を得た人と片付けられても仕方ない回ではあったと思うのですが、一応それを差し引いてもABCの3問を77分で処理できていて、これだけでも自身の過去最高水準の順位が取れており、練習・勉強を通して実力も向上してきていると自己評価して良い回だったかなと思います。
過去問の取り組みでは、一応D問題が現時点で半分以上解けていますし(短時間で解けているわけではない)、AGCの4完は必ずしも大当たり回ではなく今後もある程度実現していける水準のはず!と信じて、まだまだ上を目指していきたい。
問題A – Connection and Disconnection
Kがついていない(ひとつ文字列が与えられるだけ)のであれば簡単で、貪欲に書き換えていけばOKです。Kがついていても、左端から貪欲に書き換えていくことを考えられます。
このとき、「Sを書き換える作業を K回行う」と考えられそうですが、2周目開始時点での状況が、1周目と変わっている可能性があります。
そこで、開始地点の情報も持つようにして、
・「$n$周目を左端を書き換えなくてもよいときの操作回数と、$n+1$周目開始地点の状況」
・「$n$周目を左端を書き換える義務があるときの操作回数と、$n+1$周目開始地点の状況」
を計算すれば解けるなと思いました。
ちょっと正確に実装しきるのが面倒だぞと思います。いや、もちろんこのくらい実装しきれるべきではあるのですが…。
答を$a_K$とすると、$a_1,a_2,a_3,\ldots$ は、2つおきに等差数列であることが分かります。これは、「開始地点の状況」が2種しか存在せず、2回に1回は同じ計算をなぞる羽目になるからです(毎回同じ計算ということもある)。これに気づいて、次を実装しました。
・$a_1,\ldots,a_{10}$ を計算する。
・$K\leqq 10$ならそのまま答える。
・$K$が大きい偶数なら$a_8,a_{10}$の値から等差数列の規則で$a_K$を求める。
・$K$が大きい奇数なら$a_7,a_{9}$の値から等差数列の規則で$a_K$を求める。
実際には$a_2$まででも十分だったりすると思いますが、$K=1$まわりに例外的な何かが落ちているかどうか等をケアする必要がなく、うっかりがあっても少しでも安全になるように工夫しました。
※「小さい場合は全探索で調べて、あとは多項式の規則で補間」というようなアイデアは、(数学としてよりも)プログラミングで問題を解くことを考えるようになってから出会った手法です。Project Eulerでも、「線形漸化式があるはずだから小さい場合に調べてberlekamp massey algorithmで求めればよい」というような解法に出会うことがしばしばあって、初めてみたときはびっくりしました。
流石に間違いなく解けるレベルの問題ではあったのですが、最近意識していた「考察の中枢を乗り越えてから解ききるまでを手短にまとめる」という課題が上手く実践できて、良かったです。
問題B – Graph Partition
番号を増やすか減らすか分からないな → どちらにしても偶奇は同じだ! → 二部グラフじゃないと無理!
までは割と速かったです。「二部グラフならできるか?」→ さすがに2つの番号だけで出来ます。
というわけで、番号の種類数の最大値だけが問題になって、ここで一度行き詰まります。
仕方がないので、サンプルのグラフを全部手書きします。入力例3を眺めます。二部グラフなので頂点を左右に分けて書いてみたり、結論となる頂点番号を層にして書いてみたりします。後者のグラフが良かったですね。
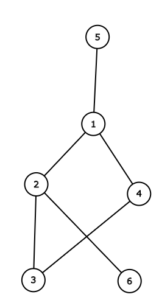
(コンテスト中は手書きした)。
「直径っぽい!」「根から見た距離で並んでる!」と思いました(「根」は木じゃないので普通使わない表現でしょうか?)。木じゃない場合の直径ってなんだ? → 最遠2点対に注目?
最遠2点対の距離を$d$として、$d+1$が最大であることが示せるかな?
→ より大きくできないことは自明だった(その2点間の移動経路に沿った番号変化を見る)
→ $d+1$が実現できるのかどうかはよく分からない。それっぽく頂点を並べたとして、番号が離れた2か所を結んでいると困っちゃう…。
→ bfs木!bfs木!辺はbfs木における近い階層の間にしかないって見たことある!
過去問の解説や、「アルゴリズムデザイン」で見覚えがある、bfs木の重要性質でした(難しい性質ではない)。ビジュアルとして、2層の間に辺が色々あるグラフ形状が頭に入っていたようです。つい先日「bfs」というワードを頻繁に目にする機会があったことも、反応を速くしたと思います。
最終的には、
・2点間の距離の最大値を求める(全2点対距離を計算 → floyd warshall)
・二部グラフかどうかを判定する(floyd warshall の結果において、同一階層の中に辺がないかどうかを調べる)
となって、実装量も少なかったです。
問題C – Division by Two with Something
何も分からなさそうに見えたので、まずは実験です。ナイーブな実装は簡単な問題だったので、入力例1, 2ともに全部計算します。観察として、「元に戻ってこないパターンはないらしい?」「周期はほとんど1種類?」ということが読み取れます。
「必ず元に戻ると証明できるかな??」
→ 一般には出次数 1 しか保証されなさそうだけど…
→ その条件下でループってことはサイクルてことは入次数 1 が保証できる事情があるってこと?
→ つまり、「逆の操作」が一意に定まるってこと?
→ 最上位を見ると証明できた(この過程で、「最上位の 0 も省略せず表記した方が良い」という認識に至った)。
しかし、まだポイントが見えてこないので、もう少し実験データをそろえたい気持ちになります。$N$と$X$を適当に設定して…と考えていると、$X$は(規則発見時点では)無関係であることに気づきます。実験はかどる~。
結局 $1\leqq N\leqq 15$ は全て計算させて、「$N$ごとにどんな周期があるのか書き出し」「短い周期になるパターンの観察」をやっていきました。
「000111000」のようなパターンがひとつの典型っぽく見える。まだ分からない。より複雑そうな短縮パターンを探して観察する。コンテスト中のノートを見返すと、「101000101110100」をいじっているときに発見があったようです。「10100 | 01011 | 10100」となっていて、「x ,invert(x), x」のパターンに見えます(invert はビット反転)。
「invert(x)」という概念を考察の中心に据えると、N回の操作でビット反転になること、2N回の操作で戻ること、周期は 2N/奇数 に限定されることなどが一気に証明できます。「x,invert(x),x,invert(x), …, invert(x),x」の必要十分性が分かった気になります。
ここで大体解けた気になりますが、まだ道半ばなので気を緩めずに詰め切ります。$X$以下という要素も含めて数え上げ方を確認。手計算で入力例1, 入力例3 が解けることを確かめる。奇数の約数は少ししかなくて…約数包除と呼ばれるパートは前回(AGC038-C)と違ってよほど下手にやっても大丈夫で…。
巨大な2進法表記の扱いは、pythonの多倍長整数に任せられます(x = int(‘1111’, 2) の要領で2進法表記文字列を整数として受け取れる)。実装量も少なくスムーズにACまで行けました。
問題D – Incenters
内心って何だっけ…弧上の3点の和ですね。(10年前なら分からないけど)現在では有名な数オリ数学です。次の書籍に記述があるため。

(競プロ界隈のアリ本のように)いま数オリを学ぶ人には最重要視されている書籍のようです。アリ本ほど完成度が洗練されているとは言い難いところもありますが、複素座標のところは他の書籍でも学べるものがなくて、そこ単体でも割と面白いと思います(いわゆる自慢、宣伝)。座標で三角形の内心を綺麗に扱う方法の記述があり、これを勉強している人には易しい問題だったようです。私にも簡単でした。
内心は角の二等分線の交点です。三角形$ABC$の角$A$の二等分線は、外接円と弧$BC$の中点で交わります(円周角の定理からすぐに分かる)。内心はこれらの垂心なのでEuler線より3点の座標を足すだけです。Euler線は中高数学の問題集でもしばしば取り上げられますし、全体を通してまぁ標準中学高校数学の範囲で十分できる考察(数オリ本選で証明を問うなら、本選1番でも易しめ?)ですが、知識として標準装備している人はやっぱり数オリ勢以外には少ないのかもしれませんね。
とはいえまぁ単純な高校数学で座標計算をする(例えば角の二等分線定理により内分2回して三角関数の和積・積和)をしてもすぐに作れる式ではあるので、「知ってれば得する問題」なだけであって「知らないと無理な問題」ではないかと思います(知らなくて数学式変形力が弱いと厳しいと思うけど、そういうのはこの問題に限らず他の問題でも随所に見られる)。

