| A | B | C | D | E | F | |
| 問題文 | ■ | ■ | ■ | ■ | ■ | ■ |
| 自分の提出 | ■ | ■ | ■ | ■ | ■ | |
| 結果 | AC | AC | AC | AC | RE |
全体感想
ABCE の 4 完で、478 位です。
F をバグらせてしまい、本番中にとりきれなくて、いまいち順位になりました。
残り30分くらいの段階で、一応 5 完はしておこうかと思って E までを解きにかかりますが、この E もなかなかくせもので、E → A → B → C と提出したところでタイムアップしました。
F は、複数箇所バグらせていて。y 座標を一意な x 座標の値と比べて座圧していたりみたいなひどすぎるミスも発覚までに時間がかかりw 最後には 94AC + 2RE まで到達したのですが、線分同士が重なる場合にバグらせていました。
バグの要因特定には、ランダム生成ケースとの愚直解法合わせをする方法がありますが、愚直解法を書くのが面倒でやりませんでした。しかし、WA はともかく RE に対するテストに関しては、ランダムケースを作成してまわす労力は十分小さく抑えられるので、やるべきだったなあと反省。
問題C – : (Colon)
余弦定理の解説で話題になっていましたね。
問題文を見て、「座標が分かるよね」と反応するか「長さとなす角が分かるよね」と反応するか、どちらも十分自然だと思うので、先に考えたもので実装すればよいでしょう。特筆すべき面倒さの違いはほとんどないと思います。
z1 = A * complex(cos(t1), sin(t1))指定の半径と偏角を持つ複素数の実装です。
z1 = A * np.exp(t1 * 1j)
$\exp(t i) = \cos t + i\sin t$ を利用して、こういう書き方もできます。
z1 = cmath.rect(A, t1)というのもあるようです。
余弦定理
余弦定理は、単純には、三角形の「二辺夾角」あるいは「三辺」が与えられたときに、他の辺の長さや角の大きさを求めるために利用できる定理です。「二角夾辺」であれば、正弦定理が使えます。合同条件に代表される三角形データの与えられ方に一通り対応できますね。
私は本問では使いませんでしたが、競プロでの使用経験は何度かあります。例えば、$2$ 円の交わり方(共通弦の長さや中心角、共通部分の面積など)を計算する際、半径・距離から必要な角度を手に入れる目的で使用できます。
問題 D – .. (Double Dots)
最短路に沿った木を作ればよくて、当然 BFS木 が条件を満たす。という問題です。
折角なので、BFS木について簡単にまとめます。連結グラフ $G$ にひとつ「根」を固定して、BFSで新しい頂点を見つけたときに、そこに辺を貼るようにして根付き木 $T$ を作ります。これをBFS 木と呼びます。
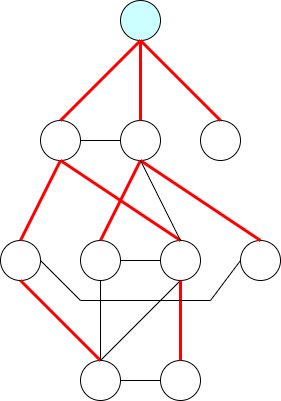
BFS木における根からの距離を「深さ」と呼ぶと、次の性質が成り立ちます。
(1) 深さが $2$ 以上異なる点の間には $G$ の辺が存在しない。
(2) 深さは $G$ における根からの距離と一致する。
BFS の探索順から容易ですね。 例えば
(1):深さ $d_1, d_2 (d_2 \geqq d_1 + 2)$ の $2$ 頂点 $v_1,v_2$ が $G$ の辺で結ばれていたとすると、$v_1$ からの BFS で $v_2$ が見つかってしまい矛盾します。
(2):(1) より辺が深さを $1$ までしか変えないことから、距離 $\geqq$ 深さです。一方 $G$ における距離は $T$ における距離以下なので、等号であることが分かります。
本問題では、BFS木に沿って「道しるべ」を置けば、「深さ」の回数で根に到達できるため、(2) よりBFS木が条件を満たします。また、本問題では問われていませんが、(1) の知識が役に立つ問題もあります。
BFS 木、DFS 木はグラフを調べる基本的なツールなので、簡単な性質(他の辺はどこにできるのかなど)はおさえておくと、時々役に立つと思います。
問題 E – ∙ (Bullet)
まず、$A_iA_j + B_iB_j = 0$ がどのくらい成り立つのかを調べる必要がありそうです。
全てのペア $(i,j)$ を個別に調べると、$\Theta(N^2)$ 時間がかかります。こういうのはまぁ、「$i$ を固定して、対象となる $j$ をまとめて扱う」という考え方が典型ですね。
$A_i, B_i$ が定数だと思って $(A_j, B_j)$ に関する条件だと思うことにすると、$\frac{A_j}{B_j} = -\frac{B_i}{A_i}$ というような式変形を考えるのは難しくないと思います。
正確には分数表記をすると、ちょっと分子または分母が $0$ の場合が厄介そうですが、方針が明確になったあとで処理を考えればよいでしょう。ひとまずは、各有理数 $r$ に対して「$r = \frac{A_i}{B_i}$ となる $i$ がいくつあるか」が手に入るようにしておくのが良さそうだとは分かります。
各有理数(あるいは射影直線 $\mathbb{P}^1(\Q)$ の元)ごとに、点の個数が集計できたとして、問題の解き方を考えます。 「有理数 $r, -1/r$ から同時に点を選んじゃいけないよ」という問題です。
これは、だいたい $r$ ごとに独立な条件ですから、$r$ ごとの場合の数を掛け合わせることで答が計算できます。ただし、$r = 1$ と $r=-1$ など、異なる $r$ が実質同じ条件に対応することがあるので、そこの二重計算をしないように気を付ける必要があります。
各 $r$ に対する問題は以下の通りです:
「グループ $A$ に $a$ 個、グループ $B$ に $b$ 個のものがある。$A, B$ 両方から 1 つ以上選ぶのはダメ。何通りの選び方があるか?」
例えば 「$A$ のみから 1つ以上とる」 「$B$ のみから 1つ以上とる」 「1つも選ばない」に場合分けして、$(2^a-1) + (2^b-1) + 1$ で計算できます。
これらの計算を各 $r$ についてやりつつ、分子分母が $0$ の場合に注意すれば完成です。また、∅は条件を満たさないという問題文になっているので、最後に $1$ を引く必要があります。
有理数 $\frac{A}{B}$ をキーとした集計を行う場合には、タプル $(A,B)$ をキーとしても上手くいきません($(1,2)$ と $(2,4)$ が区別されてしまう)。割り算して小数にしてしまうのも計算誤差で失敗します。
約分したり、分母の符号を固定したりして同じ有理数に一意な表示を固定して対応します。あるいは、巨大な素数 $p$ をとって、$\pmod{p}$ で計算する形でも、十分な確率で AC になります。
考察も、実装の細部を詰めるところも、問題 E にしてはなかなか難しめだったのではないでしょうか。
問題 F – . (Single Dot)
解説がとても短いですが、んーまあ確かに、考察は一瞬という人も多いと思います。
グリッドグラフっぽい出題であることはすぐに分かります。平面全体をマス目に区切ってあげて、隣のマスに移動できるかを考えてあげることで、グラフの連結成分の大きさを計算する問題になりそうです。
今回は制約が「$-10^9$ 以上 $10^9$ 以下」と巨大なので、そのままの座標でグリッドを作るのは無謀です。そこで、興味のある $x, y$ 座標のみを抽出する「座標圧縮」と呼ばれるテクニックを使います。今回の問題では牛さんの登場位置、線分の端点の $x,y$ 座標を集めて、番号をつけて管理します。また、外側に無限に広がる長方形領域に対応して、適当な INF, -INF を追加するのも実装において有効です。
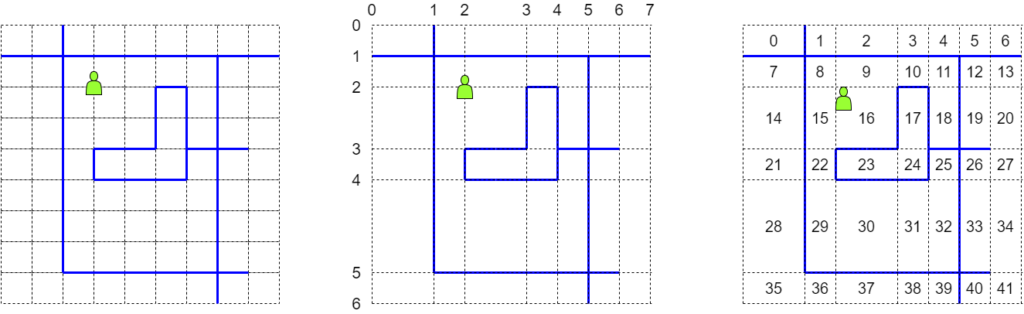
今回の問題では、牛さんの移動は格子点から格子点と考えるよりも、領域から領域への移動と思った方が良さそうです。初期位置が頂点ですが、それは適当な領域に入れてしまいましょう。
領域を、縦に $H$ 個、横に $W$ 個、合計 $HW$ 個の長方形領域に分割します。あとは各長方形を $(i,j)$ ($0\leq i < H, 0\leq j < W$)などと添字付けてしまえば、$HW$ 個の頂点からなるグラフの連結成分を調べる問題になります。個人的には、$0$ から $HW$ の $1$ 次元の添字を好んで使います($4$ つの移動は、$\pm1$, $\pm W$ となります)。
地味に、通行止めの実装に悩み。はじめ移動可能方向を隣接リストで作って通行止めを削除していきましたが、効率は悪かったです(効率は関係ないけど、ここで同じ値を 2 回削除するバグを踏んでいました)。どの頂点からも $4$ 方向の移動があるので、$N\times 4$ の配列で管理すると簡潔ですね。
$N, M=1000$ で計算量 $\Theta((N+M)^2)$ とはいえ、$4\cdot 3000^2 > 10^{7.5}$ くらい辺があるグラフの探索なので、ABC コンテストの中では要求されている計算量がやや大きめでした。 Python を使う場合には、numba, PyPy, Cython などから適切な手段を選ぶことになると思います。例えば Python + numba (AOT) で 357ms になりました(https://atcoder.jp/contests/abc168/submissions/13359130)。
なるほどなー。中途半端に出っ張ってる線分は捨てちゃえばいいと(交点のできうる座標にしか興味を持たなくてよい)。頂点数が $9$ 倍減るので、結構な定数倍改善になりそうですね。ソートがあるので、$O(NM + N\log N + M\log M)$ が正しそうです。
→ (131ms) https://atcoder.jp/contests/abc168/submissions/13389928
numpy の import に 100ms 程度かかっていることを除けば、他言語の最速付近と比べても遜色ない実行時間ですね。

