| |
A |
B |
C |
D |
E |
F |
| 問題文 |
■ |
■ |
■ |
■ |
■ |
■ |
| 自分の提出 |
■ |
■ |
■ |
■ |
■ |
■ |
| 結果 |
AC |
AC |
AC |
AC |
AC |
AC |
全体感想
36分6完1ペナで、64位でした。
わりと良い出来だと思ったのですが、上位陣はえぇ。
特に、簡単回という印象はないのですが、最速タイムで見てもAC人数で見ても人数が多いですね。すごい。強いて言うなら、Dはいつにも増して基本問題でした。
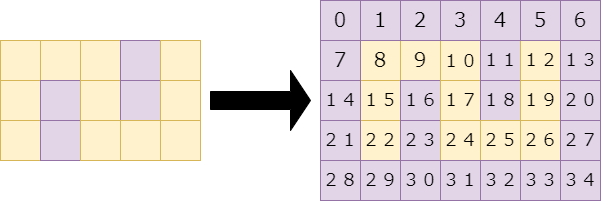
問題D – Maze Master
基本の幅優先探索です。単一始点最短経路問題を全点について解きます。
関連問題:ABC 007-C 幅優先探索
1回の移動コストが 0 または 1 である場合には、優先度付きキュー(heapq)を使わずとも deque で距離順を維持できることに注意しましょう。
また私は、グリッドグラフは、基本的には番兵を入れて、さらに1次元化して扱っています。扱う量の次元を減らせるので好んでいますが、好みの違いレベルだと思います。
$H,W$ を問題文の値よりも $2$ 増やして、最初と最後の行に壁を追加。各行の前後に壁を追加です。移動は、座標を $\pm 1, \pm W$ のいずれかだけ変化させます。
番兵を入れる利点としては、配列外参照が自動的に防げるからです。常に壁でないところから出発するようにすれば、
・if (移動先がグリッド内) and (移動先が壁でない)
としなければいけないところが
・if ( 移動先が壁でない )
だけで済みます。コードが簡略化されるだけでなく、評価する条件が減る分、パフォーマンスの地味な定数倍改善です。(マス目の個数は増えますが、これは、$H$ が $H+2$ になったりするだけなので、十分大きな $H,W$ に対しては定数倍より影響が少ないです)。
問題E – Max-Min Sums
$\sum_{S} f(S) = \sum_{S}\bigl(\max(S) – \min(S)\bigr)$ を求める問題です。和の順序をうまく入れ替えるという典型テクニックがあり、今回もそれを使います。
$\sum_{S} f(S) = \bigl(\sum_{S}\max(S)\bigr) – \bigl(\sum_S\min(S)\bigr)$ と見ることにしましょう。$\max$ と $\min$ の2通りありますが、これらはどうせ同じような計算手順になります
(例えばすべての数を $-1$ 倍すると順序が逆になって $\max$ と $\min$ が入れ替わる)。よって、本質的には「$\sum_S\max(S)$ を計算せよ」が解ければよいことになります(いかにも元の問題より易しくなりました)。
$\max(S)$ の値の候補は、数列 $A$ の元で、高々$N$ 通りしかありません。これは、部分列 $S$ の取り方より小さいです。そこで集計軸を数列 $A$ に変えて、\[ \sum_S\max(S) = \sum_{1\leq i\leq N} a_i\cdot (\max(S) = a_i となる S の個数)\] と見てあげます………。
ちょっとバグがありますね。
$\max(S)$ は整数であって、「数列の何番目」という情報は持っていません。例えば $A = [1,10,2,3,10]$ の部分列 $S = [10,2,10]$ に対して、$\max(S)$ がどちらの $10$ を指しているのか不明瞭です。
ただ、これは実際には問題になりません。このようなときには代わりに十分小さな正実数 $\varepsilon$ をとって、 $A = [1,10,2,3,$ $10+\varepsilon$ $]$ に取り換えた問題を解きます(「微小な摂動を加えることを考えて」といった形で、解説でもたまにでてきます)。$A = [1,10,2,3,10.00001]$ といった要領です。そのときの答において $\varepsilon \to 0$ とすれば元の問題の答と一致します。よって、$\max$ がどの項かが定まらないような場合は考察から除外できます。
別の見方も述べておきます。「同一の値があるときは、右側を必ず $\max$ として選ぶことにする」といった定義を加えて、$\max$ の値を数列の項に紐づけてあげればよいです。
結局、すべての項が相異なるときに、$(\max(S) = a_i となる S の個数)$ が評価できればよいです。$a_i$ の上位は選べず、下位は個数 $K$ の制約を除き自由に選べるので、この値は簡単な二項係数に一致します。
問題F – Enclose All
最適解をとって構造を観察すると、円の中心は$2$ 点の中点または $3$ 点の外心だと分かります。
※ 「最適解の存在」の存在は、有界閉集合上の連続関数が最大値を持つことから分かります。初心者はあまり気にしないでよいと思います。
これで候補が十分少なくなるので、あとは全探索します。
外心の計算について、複素座標による立式を述べます。座標幾何を複素座標で取り扱う方法は高校数学ではマイナー分野ですが、1点の座標が $(x,y)$ ではなく $1$ つの数 $z$ で書けるため、とても便利です。数オリ界では10年前くらいから急激に注目され始めた考え方で、
『獲得金メダル! 国際数学オリンピック メダリストが教える解き方と技』
で丁寧に扱われています(せんでん)。
$3$ 点 $z_1,z_2,z_3$ の外心を求めます。平行移動します。つまり $a = z_2 – z_1$, $b = z_3 – z_1$ として、$0, a, b$ の外心を求めればよいです。方程式 $|z|^2 = |z-a|^2 = |z-b|^2$ を解けばよいです。展開して $|z|^2$ を引くと、
\[\begin{align*} \overline{a}z+a\overline{z} &= a\overline{a},\\ \overline{b}z+b\overline{z} &= b\overline{b}\end{align*}\]
を解けばよいです。$z, \overline{z}$ に関する連立1次方程式とみると、$z = \frac{ab(\overline{a}-\overline{b})}{b\overline{a}-a\overline{b}}$ が分かります。
最後に、平行移動した分を戻すことを忘れないようにしましょう(1ペナ)。
なお、複素数は、Python では $z = x + y * 1j$ の要領で定義して扱うことができます。虚数単位は $j$ です。
※ 最小包含円という有名問題で、さらに効率よく計算できるようです。